Integrating Maamba and Transformer for Long-Short Range TSF

Integrating Maamba and Transformer for Long-Short Range TSF

Contents

1. Abstract
2. Preliminaries
3. Methodology
   1. Overview
   2. Embedding Layer
   3. Mamba Pre-processing Layer
   4. MambaFormer Layer
   5. Forecasting Layer
4. Experiments

0. Abstract

MambaFormer

• Mamba (for LONG range dependency)
• Transformer (for SHORT range dependency)

1. Preliminaries

(1) Problem Statement

• \(\mathcal{L}=\left(\mathrm{x}_1, \mathrm{x}_2, \ldots, \mathrm{x}_L\right)\) with length \(L\),
  • where each \(\mathbf{x}_t \in \mathbb{R}^M\) at time step \(t\) is with \(M\) variates
• \(\mathcal{F}=\left(\mathbf{x}_{L+1}, \mathbf{x}_{L+2}, \ldots, \mathbf{x}_{L+F}\right)\) with length \(F\). B
• \(\left(c_1, c_2, \ldots, c_L\right)\) : Temporal context information with dimension \(C\)
  • assumed to be known ( e.g. day-of-the-week and hour-of-the-day )

(2) SSM

a) Continuous version

\(\begin{aligned} h_t & =\overline{\mathrm{A}} h_{t-1}+\overline{\mathrm{B}} x_t \\ y & =\mathrm{C} h_t \end{aligned}\).

• where \(\mathrm{A} \in \mathbb{R}^{N \times N}, \mathrm{~B} \in \mathbb{R}^{N \times 1}\), and \(\mathrm{C} \in \mathbb{R}^{1 \times N}\) are learnable matrices.
• discretized from continuous signal into discrete sequences by a step size \(\Delta\).

b) Discrete version

• Discrete parameters \((\overline{\mathrm{A}}, \overline{\mathrm{B}})\)
  • can be obtained from continuous parameters \((\Delta, \mathrm{A}, \mathrm{B})\)
  • via zero-order hold \((\mathrm{ZOH})\) rule
• \(\overline{\mathrm{A}}=\exp (\Delta \mathrm{A}), \overline{\mathrm{B}}=\exp (\Delta \mathrm{A})^{-1}(\exp (\Delta \mathrm{A})-\) I) \(\Delta\) B.

c) Inference

\(\begin{aligned} \overline{\mathbf{K}} & =\left(\mathbf{C} \overline{\mathbf{B}}, \mathbf{C} \overline{\mathbf{A B}}, \ldots, \mathbf{C} \overline{\mathbf{A}}^k \overline{\mathbf{B}}, \ldots\right) \\ y & =x * \overline{\mathbf{K}} \end{aligned}\).

• where \(\overline{\mathbf{K}}\) is a convolutional kernel.

2. Methodology

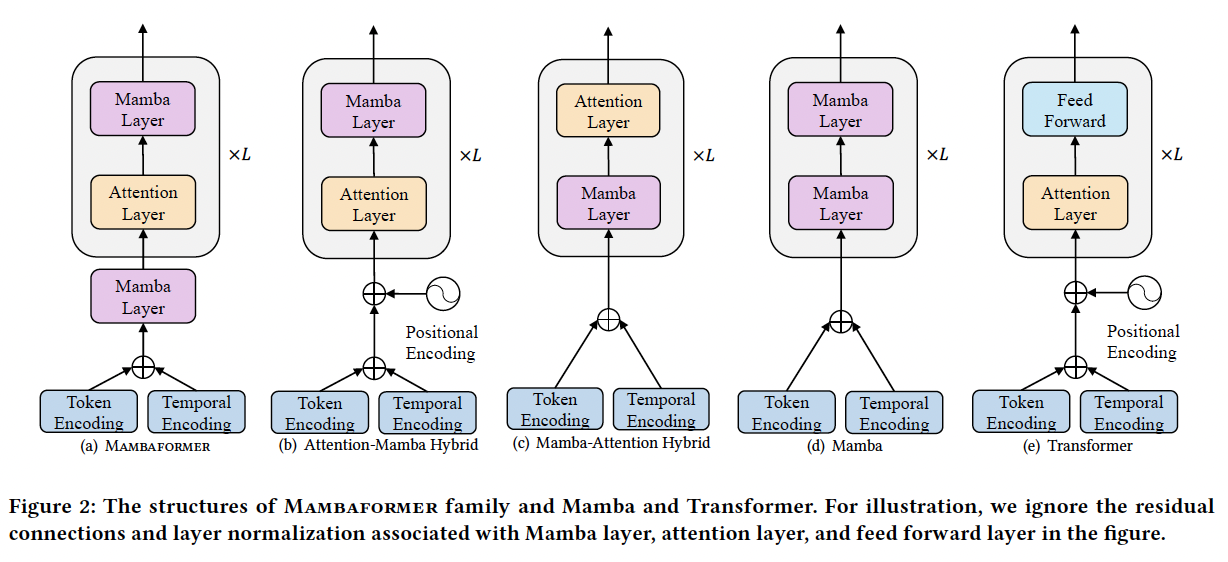
(1) Overview of MambaFormer

Hybrid architecture

• Mamba + Transformer
• adopts Decoder-only style

(2) Embedding Layer

a) Token Embedding

Raw TS \(\rightarrow\) Embed via 1d CNN

• capture locla information

b) Temporal Embedding

Numerical value + Temporal context information

Notation

• Input sequence: \(\mathrm{X} \in \mathbb{R}^{B \times L \times M}\)
• Associated temporal context: \(C \in \mathbb{R}^{B \times L \times C}\)

Embedding layer

• \(\mathrm{E}=E_{\text {token }}(\mathrm{X})+E_{\text {tem }}(\mathbf{C})\).
  • where \(\mathrm{E} \in \mathbb{R}^{B \times L \times D}\) is output embedding
  • \(E_{\text {token }}\) and \(E_{\text {tem }}\) : token embedding layer & temporal embedding layer
• No need for positional embedding

(3) Mamba Pre-processing Layer

Mamba pre-processing block

• \(\mathrm{H}_1=\operatorname{Mamba}(\mathbf{E})\).
  • where \(\mathrm{H}_1 \in \mathbb{R}^{B \times L \times D}\) is a mixing vector
  • including token embedding, temporal embedding, and positional information.

(4) MambaFormer Layer

a) Attention Layer

For SHORT-range time series dependencies in the transformer

\(\rightarrow\) Use masked multi-head attention layer to obtain correlations between tokens

• Masking mechanism: to prevent positions from attending to subsequent positions

(Head \(i=1,2, \ldots, h\))

Transforms the embedding \(\mathrm{H}_1\) into…

• (Q) queries \(\mathbf{Q}_i=\mathrm{H}_1 \mathbf{W}_i^Q\),

• (K) keys \(\mathbf{K}_i=\mathbf{H}_1 \mathbf{W}_i^K\),
• (V) values \(\mathbf{V}_i=\mathbf{H}_1 \mathbf{W}_i^V\),

where \(\mathbf{W}_i^Q \in \mathbb{R}^{D \times d_k}\), \(\mathbf{W}_i^K \in \mathbb{R}^{D \times d_k} \in\), and \(\mathbf{W}_i^V \in \mathbb{R}^{D \times d_v}\) are learnable matrices.

Output: \(\mathrm{O}_i=\operatorname{Attention}\left(\mathrm{Q}_i, \mathrm{~K}_i, \mathrm{~V}_i\right)=\operatorname{softmax}\left(\frac{\mathrm{Q}_i \mathrm{~K}_i^T}{\sqrt{d_k}}\right) \mathrm{V}_{\mathrm{i}}\).

• outputs \(\mathrm{O}_i\) of each head are concatenated into a output vector \(\mathbf{O}\)
  • with the embedding dimension \(h d_v\).

Projection

• Projection matrix \(\mathbf{W}^O \in \mathbb{R}^{h d_v \times D}\)
• Output of attention layer \(\mathbf{H}_2=\mathrm{OW}^O \in \mathbb{R}^{B \times L \times D}\).

b) Mamba Layer

Incorporate the Mamba layer

• to overcome computatiaonal challenges of the Transformer

**Mamba block **

• Sequence-sequence module
  • with the same dimension of input and output
• Procedure
  • (1) Takes an input \(\mathrm{H}_2\)
  • (2) Expand the dimension by two input linear projection
    • Projection 1)
      • Processes the expanded embedding through a convolution and SiLU activation before feeding into the SSM.
      • Goal: Select input-dependent knowledge and filter out irrelevant information.
    • Projection 2)
      • Followed by SiLU activation ( as a residual connection )
      • As a multiplicative gate
  • (3) Output \(\mathrm{H}_3 \in \mathbb{R}^{B \times L \times D}\)

(5) Forecasting Layer

\(\widehat{\mathrm{X}}=\text { Linear }\left(\mathrm{H}_3\right)\).

• where \(\widehat{\mathbf{X}} \in \mathbb{R}^{B \times L \times M}\)

3. Experiments