생존 분석 (Survival Analysis) 기초

생존 분석 (Survival Analysis) 기초

Contents

1. 생존분석이란?

2. 생존분석의 함수들

3. 중도 절단

4. 생존분석이 풀고자하는 문제들

5. Kaplan-Meier 추정 방법

6. C-index

7. RNN-Surv : A Deep Recurrent Model for Survival Analysis

1. 생존분석이란?

생존 분석 :

• 어떠한 사건(event)이 발생하기 까지 걸리는 시간에 대한 분석
• ex) 생명체의 “관찰 시작~사망”까지의 시간
• 대표적 방법론 : Kaplan-Meier 추정 방법, Cox 비례 위험 모형

생존 함수 (Survival Function) : \(S_t\)

• \(S(t)=\operatorname{Pr}(T>t)\).
  • \(t\) : 시간 변수
  • \(T\) : 사망 시점
• 의미 : “특정 시간 \(t\)보다 오래 생존할 확률”
• 특징
  • 1) \(S(0)=1\).
  • 2) 단조 감소 함수 : \(S(u) \leq S(t)\) if \(u \geq t\).
  • 3) 시간의 흐름에 따라 0으로 수렴

2.생존분석의 함수들

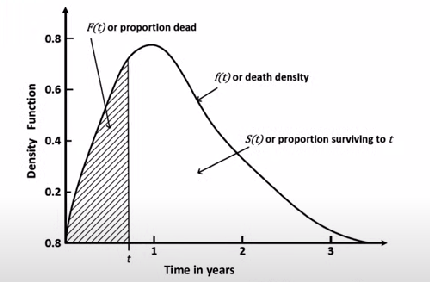
사건 분포 함수 (Lifetime Distribution Function) : \(F(t)\)

( = 누적 사망분포 함수 (Cumulative Death Distribution Function))

• \(F(t)=\operatorname{Pr}(T \leq t)=1-S(t)\).
• 의미 : “특정 시간 \(t\)이전에 사망할 확률”

생존 분포의 밀도 : \(f(t)\)

( = 사망 밀도 함수 (Death Density Function) )

• \(f(t)=F^{\prime}(t)=\frac{d}{d t} F(t)\).
• 의미 : 단위 시간 당 사망 비율

\(S(t)\) & \(F(t)\) & \(f(t)\)의 관계식

• \(S(t)=\operatorname{Pr}(T>t)=\int_{t}^{\infty} f(u) d u=1-F(t)\).

위험 함수 (Hazard Function) : \(h(t)\)

• \(h(t)=\lim _{d t \rightarrow 0} \frac{\operatorname{Pr}(t \leq T<t+d t)}{d t \cdot S(t)}=\frac{f(t)}{S(t)}=-\frac{S^{\prime}(t)}{S(t)}\).
• 의미 : \(t\)시점까지 생존했다는 가정 하에, \(t\)시점에 관심 사건이 발생할 확률

누적 위험 함수 (Cumulative Hazard Function) : \(H(t)\)

• \(H(t) = \int_{0}^{t}h(u)du\).

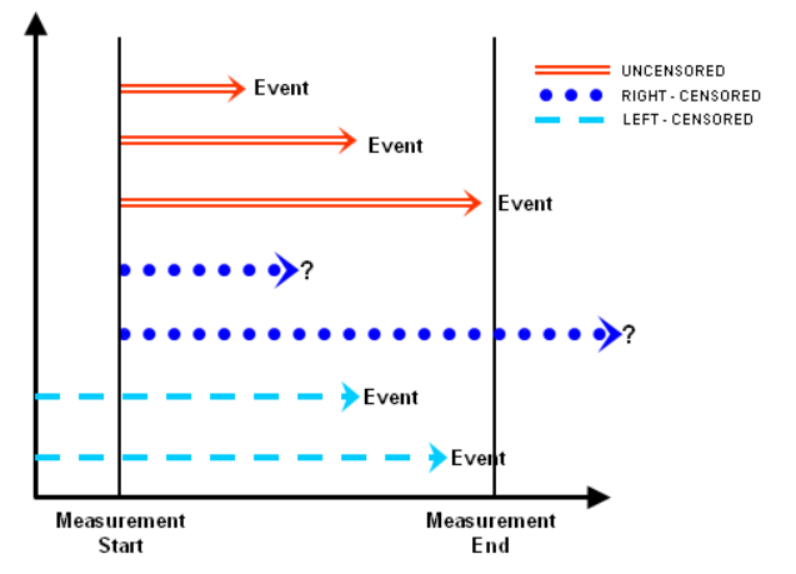
3. 중도 절단

손실된 데이터를 처리하는 방법

2종류의 censoring

• right censoring :
  • 1) 연구 종료 전에, “다른 이유로 사망”
  • 2) 연구 종료 “후에도 생존”
• left censoring :
  • 1) 연구 **시작 ** 전에, “이미 질환을 보유”했던 경우

4. 생존분석이 풀고자하는 문제들

• Q1) 특정 병에 걸린 환자가 \(n\)년 이상 생존할 확률은?
  • A1) \(S(n)\)
• Q2) 택시를 잡기까지 기다려야 하는 시간은?
  • A2) 중위수 \(t\) 시간
• Q3) 구직자 \(K\) 명이, \(a\)년 후에 직장을 구했을 예상 사람 수는?
  • A3) \(K \times S(a)\) 명

5. Kaplan-Meier 추정 방법

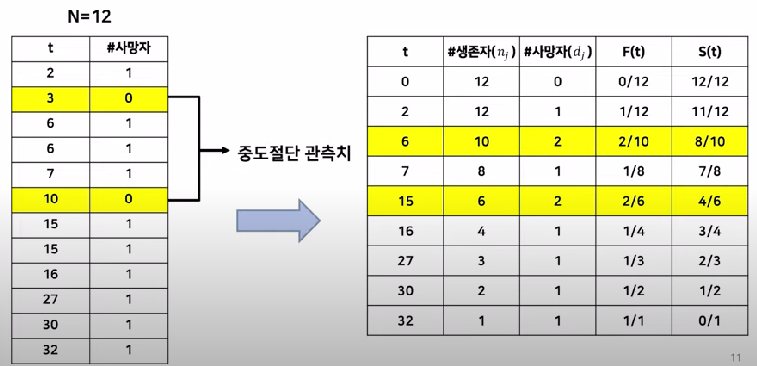
Kaplan-Meier 추정 방법

• “관찰 시간”에 따라, 사건이 발생한 시점의 “사건 발생률”을 계산
• 이론 : \(S(t)=1-F(t)=\operatorname{Pr}(T>t)\)
• 추정 : \(\hat{S}(t)=\prod_{i ; t_{i}<t} \frac{n_{i}-d_{i}}{n_{i}}\)
• Notation
  • \(n_i\) : 시점\(i\)의 관측 점수
  • \(d_i\) : 시점\(i\)의 사건 발생 건수

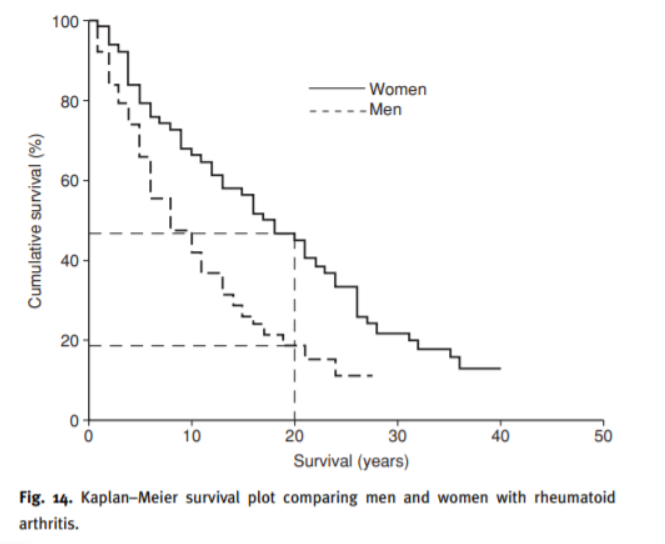
Survival Plot

Example :

test_df <- tribble(~time, ~censor, 
143,    1, 
165,    1, 
188,    1, 
188,    1, 
190,    1, 
192,    1, 
206,    1, 
208,    1, 
212,    1, 
216,    0, 
216,    1, 
220,    1, 
227,    1, 
230,    1, 
235,    1, 
244,    0, 
246,    1, 
265,    1, 
303,    1)

Kaplan-Meier Survival Estimates : \(\hat{S}(t)=\prod_{i ; t_{i}<t} \frac{n_{i}-d_{i}}{n_{i}}\).

• \(\hat{S}(143)=\frac{19-1}{19}=0.947368\).

• \(\hat{S}(165)=0.947368 \times \frac{18-1}{18}=0.894737\).
• \(\hat{S}(188)=0.894737 \times \frac{17-2}{17}=0.7894738\).
• …
• \(\hat{S}(303)=0.078947 \times \frac{1-1}{1}=0\).

6. C-index ( Concordance Index )

• Survival Analysis에서 많이 사용하는 정확도 지표

• 여러 대상의 생존 시간(또는 위험)을 상대적으로 비교

  ( 사망 “순서”를 잘 예측하는지 판단 )

Concordance probability

• \(c=\operatorname{Pr}\left(\hat{y}_{1}>\hat{y}_{2} \mid y_{1} \geq y_{2}\right)\).
  • \(y_i\) : 사건이 실제로 발생한 시간
  • \(\hat{y_i}\) : 모델의 예측 시간

C-index

• \(\hat{c}=\frac{1}{P^{\prime}} \sum_{i: \delta_{i}=1} \sum_{j: y_{i}<y_{j}} I\left[S\left(\hat{y}_{i} \mid X_{i}\right)<S\left(\hat{y}_{j} \mid X_{j}\right)\right]\).

7. RNN-Surv : A Deep Recurrent Model for Survival Analysis

RNN-SURV: A Deep Recurrent Model for Survival Analysis

RNN-Surv = RNN + Survival Analysis

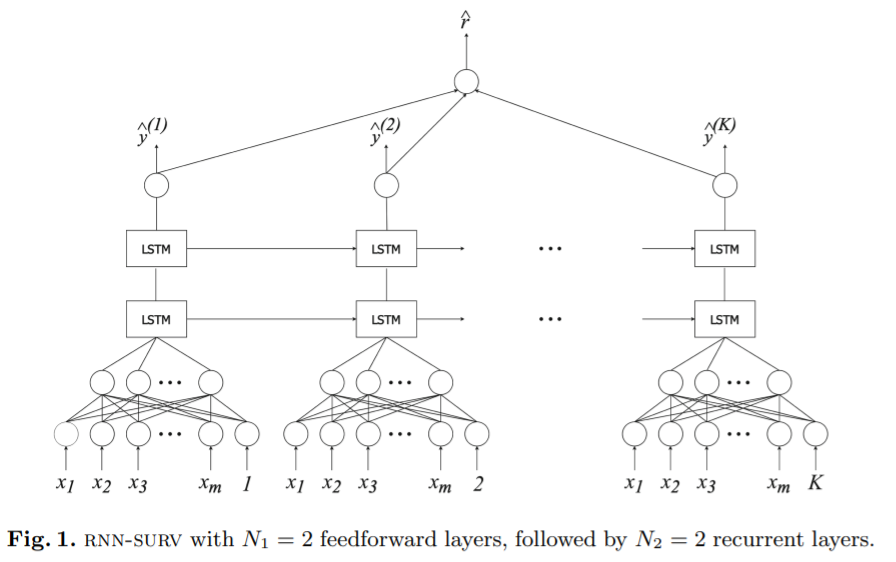
• divide into \(K\) interval :
• goal : output both
  • 1) estimate \(\hat{y_i}^{(k)}\) of survival probability \(S_i\) for the \(k\)th time interval
  • 2) risk score : \(\hat{r}_{i}=\sum_{k=1}^{K} w_{k} \hat{y}_{i}^{(k)}\)
    • \(w_k\) : parameters of the last layer

Loss Function

• (1) for \(\hat{y_i}^{(k)}\) ( modified CE ) : \(\mathcal{L}_{1}=-\sum_{k=1}^{K} \sum_{i \in U_{k}}\left[I\left(Y_{i}>t_{k}\right) \log \hat{y}_{i}^{(k)}+\left(1-I\left(Y_{i}>t_{k}\right)\right) \log \left(1-\hat{y}_{i}^{(k)}\right)\right]\)

• (2) for risk-score \(\hat{r}_{i}\) ( negative c-index의 상한 ):

  \(\mathcal{L}_{2}=-\frac{1}{ \mid \mathcal{C} \mid } \sum_{(i, j) \in \mathcal{C}}\left[1+\left(\frac{\log \sigma\left(\hat{r}_{j}-\hat{r}_{i}\right)}{\log 2}\right)\right]\).

Reference

• https://ko.wikipedia.org/wiki/%EC%83%9D%EC%A1%B4%EB%B6%84%EC%84%9D
• https://namu.wiki/w/%EC%83%9D%EC%A1%B4%20%EB%B6%84%EC%84%9D
• https://bioinformaticsandme.tistory.com/223
• http://aispiration.com/ml/ml-pm-survival.html
• https://hyperconnect.github.io/2019/10/03/survival-analysis-part3.html
• https://www.youtube.com/watch?v=uRr4YFsJPqw