Channel-Awaare Low-Rank Adaptation in Time Series Forecasting

Channel-Awaare Low-Rank Adaptation in Time Series Forecasting

Contents

1. Abstract
2. Preliminaries

0. Abstract

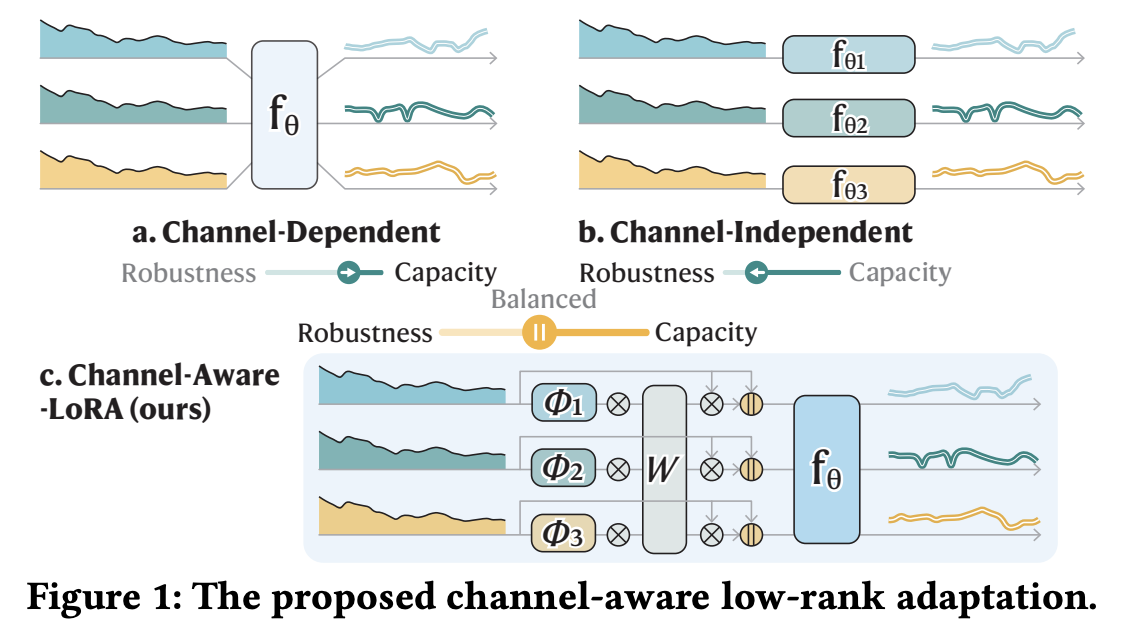
Channel-aware low-rank adaptation

• To balance CI & CD
• How? Condition CD models on identity-aware individual components
• Plug-in solution

1. Introduction

a) Limitation of existing approaches

Group-aware embedding [18]

Inverted embedding [9] for Transformers

Leading indicator estimation [22]

Channel clustering [1]

$\rightarrow$ Either limited to specific types of backbone model

b) Our solution

Background) Low-rank adaptation [5]

Proposal) Channel-aware low-rank adaptation (C-LoRA)

• Trade-off between the two strategies
• Provide an alternative in a parameter-efficient way

Parameterize each channel a low-rank factorized adapter to consider individual treatment

Specialized channel adaptation is conditioned on the series information to form an identity-aware embedding

c) Contribution

• Plug-in solution
  • Adaptable to a wide range of SOTA TS model
  • No changes to the existing architecture
• Extensive experiments
  • Improve the performance of both CD and CI backbones
  • Great efficiency, flexibility to transfer across datasets, and can enhance channel identity

2. Methodology

(1) Backbone

General forecasting template

• for both the CI and CD models

Step 1) $\overline{\mathbf{X}}=\operatorname{Normalization}(\mathbf{X})$.

• ex) ReviN: to address the nonstationarity of TS

Step 2) $\mathbf{z}c^{(0)}=\operatorname{TokenEmbedding}\left(\overline{\mathbf{X}}{;}, c\right)$

• $\forall c=1, \ldots, C $.
• usually implemented by MLPs to process temporal features

Step 3) (Optional) $\mathbf{Z}^{(\ell+1)}=\operatorname{ChannelMixing}\left(\mathbf{Z}^{(\ell)}\right)$

• $\forall \ell=0, \ldots, L$.
• optional for CD models by Transformer blocks or MLPs.

Step 4) $\widehat{\mathbf{Y}}=\operatorname{Projection}\left(\mathbf{Z}^{(L+1)}\right)$.

• usually implemented by MLPs to process temporal features

(2) C-LoRA

Revisiting the two strategies

a) CI strategy)

Individual models for each channel

• Instantiate the TokEnEmbedding with a series of mappings, e.g., different MLPs: $\mathbf{z}c^{(0)}=\operatorname{MLP}_c\left(\overline{\mathbf{X}} ; \theta_c\right), \forall c=1, \ldots, C$.

• Hypothesis class of all individuals

  • $\mathcal{H}_{\mathrm{CI}}={\operatorname{MLP}_c\left(\cdot ; \theta_c\right) \mid \theta_c \in \Theta, c=1, \ldots, C}$.

  $\rightarrow$ However, such a hypothesis class is computationally expensive

  ( + Pure CI models fail to exploit multivariate correlational structures )

b) CD strategy

Expressive by modeling channel interactions

• either explicitly with ChannelMixing or implicitly by optimizing the global loss in Eq. (1).

Limitation

• (1) Have difficulty capturing individual channel patterns with a shared encoder $\operatorname{MLP}(\overline{\mathbf{X}} ; \theta)$,

• (2) CM operation

  • can generate mixed channel identity information

    $\rightarrow$ Cause an indistinguishment issue [11]

c) Combine CI + CD

Channel-wise adaptation in a CD model

Model individual channels in a parameter-efficient way

$\rightarrow$ Low-rank adapter

• Specialized for each channel $\phi^{(c)} \in$ $\mathbb{R}^{r \times D}$, where $r \ll D$ is the intrinsic rank.

How? Condition on another low-rank matrix

• $\widetilde{\phi}^{(c)}=\operatorname{ReLU}\left(\phi^{(c), \mathrm{T}} \mathbf{W}\right) \in \mathbb{R}^{D \times d}$.
  • $\mathbf{W} \in \mathbb{R}^{r \times d}$,
  • $d$ : adaptation dimension.
  • $\widetilde{\phi}^{(c)}$ : channel-specific parameters
    • Needs to be aware of the series information to consider the channel identity.

Result: $\mathbf{z}_{c, \phi}^{(0)}=\mathbf{z}_c^{(0), \mathrm{T}} \widetilde{\phi}^{(c)} \in \mathbb{R}^d$ - where $\mathbf{z}_c^{(0)}=\operatorname{MLP}\left(\overline{\mathbf{X}}_{:, c} ; \theta\right)$ is obtained by a CD model shared by all channels
Aggregate all channel adaptations $\mathbf{Z}_\phi^{(0)}=\left\{\mathbf{z}_{c, \phi}^{(0)}\right\}_{c=1}^C \in \mathbb{R}^{C \times d}$ Incorporate it into the global CD models
Final C-LoRA: $\mathbf{Z}^{(0)}=\left[\operatorname{MLP}(\overline{\mathbf{X}} ; \theta) \| \mathbf{Z}_\phi^{(0)}\right] \in \mathbb{R}^{C \times(D+d)}$.
Summary - Balance between CD and CI models - Efificiently integrates global-local components - Adapt to individual channels with the specialized channel adaptation $\mathbf{z}_{c, \phi}^{(0)}$ &Preserve multivariate interactions by the shared $\operatorname{MLP}\left(\overline{\mathbf{X}}_{i, c} ; \theta\right)$. - Reduced hypothesis class is $\mathcal{H}_{\mathrm{C} \text {-LoRA }}=$ $\left\{\operatorname{MLP}\left(\cdot ; \theta, \phi^{(c)}\right) \mid \theta \in \Theta, \phi^{(c)} \in \mathbb{R}^{r \times D}\right\}$,