Metadata Matters for Time Series; Informative Forecasting with Transformers

Metadata Matters for Time Series; Informative Forecasting with Transformers

Contents

1. Abstract

2. Introduction

3. Related Works

   1. Finetuning LLMs

   2. Freeze LLM, align TS data with NL

4. Method
   1. Informative TS Forecasting
   2. Metadata Embedding
   3. MetaTST

0. Abstract

Metadata carries valuable information!

MetaTST

Metadata-informed Time Series Transformer

• incorporate multiple levels of context-specific metadata
• formalizes metadata into natrual languages (by predesigned templates)
• leverages LLMs to encode these texts into metadata tokens

Unlike previous LLM-TS models, use LLM as “fixed metadata encoder”

1. Introduction

Metadata

= descriptions about dtata

= data source details, statistical summaries ..

Characteristics of metadata

• usually unstructured
• contains information from heterogeneious views

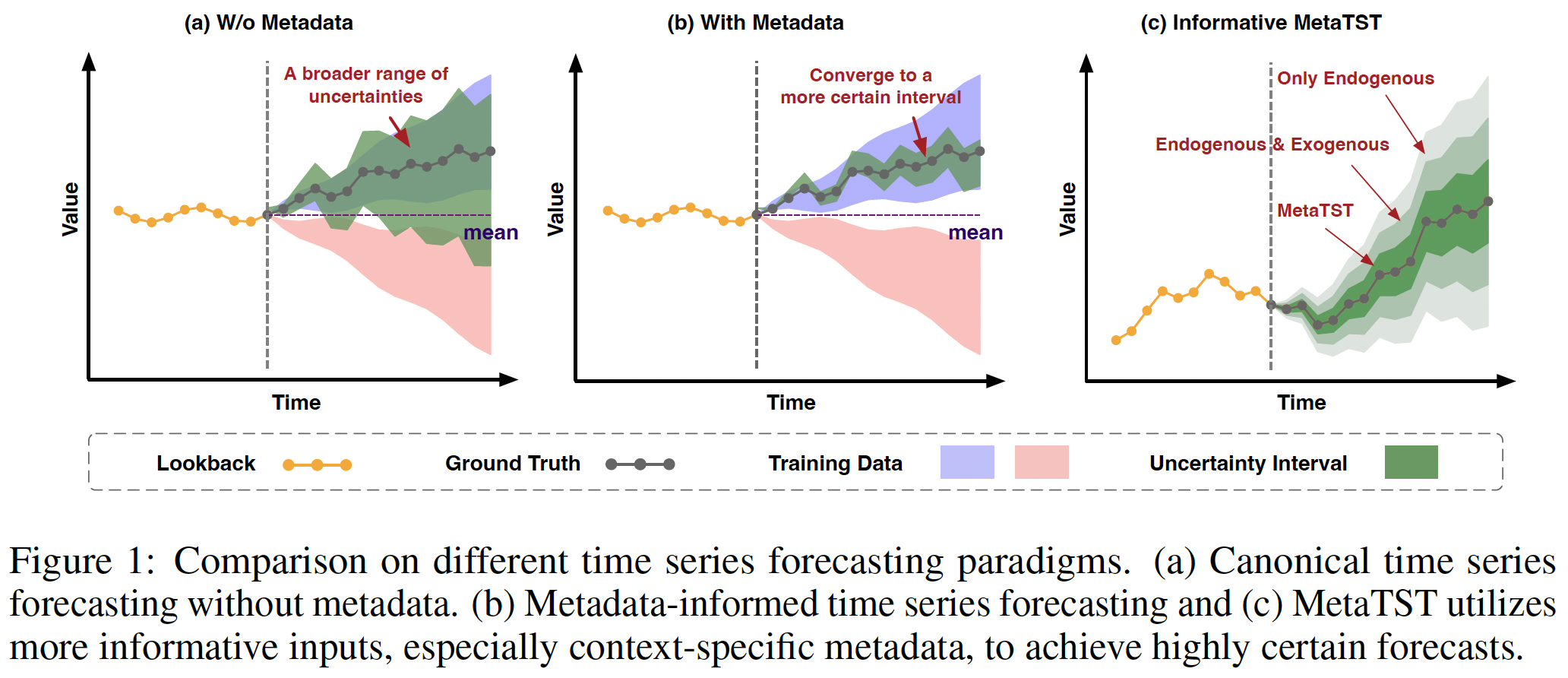
Three key elements for accurate forecasting

• (1) Endogenous series
• (2) Exogenous series
• (3) Metadata

2. Related Works

LLM for TS

Briding gap between TS & Text

1. Fine-tuning LLMs

2. Freeze LLM, align TS data with NL

(1) Fine-tuning LLMs

• GPT4TS (2023): Fine-tune PE & LN in transformer (GPT2)
• LLM4TS (2023): Two stage fine-tuning to adapt LLMs to TS

(2) Freeze LLM, align TS data with NL

• TimeLLM (2024): Reprogram input TS with text prototypes
• AutoTime (2024): Independently embeds TS into latent space of LLM & train new projection layers for TS

Previous works takes LLM as “backbone” for prediction

\(\leftrightarrow\) MetaTST leverages LLM as “plug-in encoders” for context-specific metadata.

3. Method

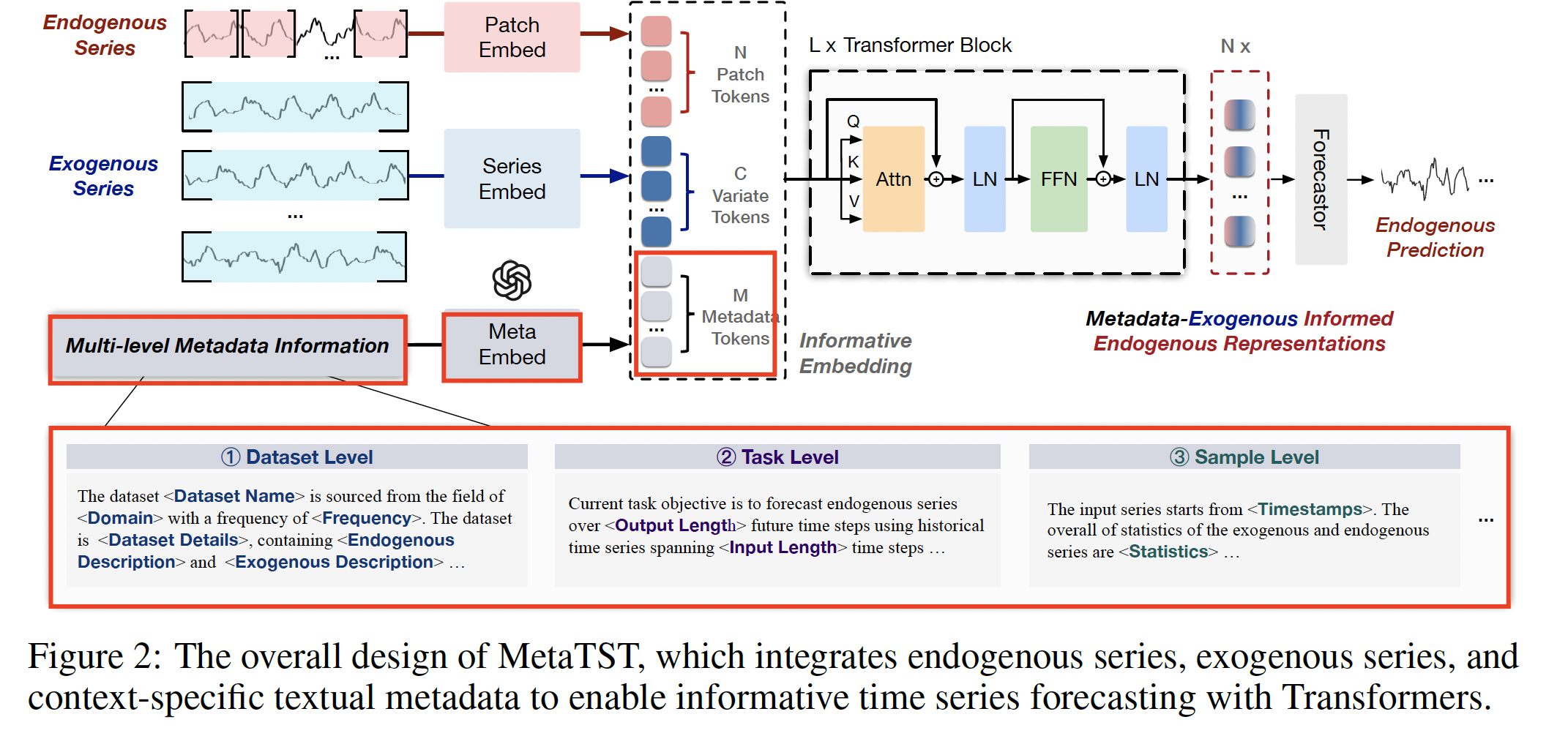
(1) Informative Time Series Forecasting

Notation

• (1) Historical observations: \(\mathbf{x}_{\mathrm{en}} \in \mathbb{R}^{T_{\mathrm{en}}}\)
• (2) Relevant exogenous series: \(\mathbf{x}_{\mathrm{ex}}=\left\{\mathbf{x}_{\mathrm{ex}, 1}, \mathbf{x}_{\mathrm{ex}, 2}, \ldots, \mathbf{x}_{\mathrm{ex}, C}\right\} \in \mathbb{R}^{T_{\mathrm{ex}} \times C}\)
• (3) Corresponding metadata \(\mathbf{x}_{\text {meta }}\)
  • Readily available in real-world applications,

Objective function

• \(\underset{\theta}{\arg \min } \mid \mid \mathbf{y}_{\mathrm{en}}-\mathcal{F}_\theta\left(\mathbf{x}_{\mathrm{en}}, \mathbf{x}_{\mathrm{ex}}, \mathbf{x}_{\mathrm{meta}}\right) \mid \mid _2^2\).

(2) Metadata Embedding

“Unstructured” metadata \(\rightarrow\) “Structured” NL template

• via Multi-level metadata parser

a) Multi-level Metadata parser

Three types of tokens to incorporate metadata

• (1) Dataset
  • Essential properties about the dataset
  • e.g., domian and sampling frequency
• (2) Task
  • Description of the task
  • e.g., target of interest, the length of input and output TS
• (3) Sample
  • Dynamic statistics of TS
  • e.g, start timestamps, mean, std …

\(\left\{\widehat{\mathbf{x}}_{\text {meta }, k}\right\}_{k=1}^M=\text { MetaParser }\left(\mathbf{x}_{\text {meta }}\right)\).

• \(M\): information levels, which is set as 3 (for dataset, task and sample aspects)

b) LLMs as the Metadata Encoder

(1) Any LLM can be used!

• e.g., auto-regressive LLMs (Llama, GPT), encoder-type LLMs (T5, BERT)

(2) Aggregtaion

• Word-level tokens \(\rightarrow\) Requires aggregation!

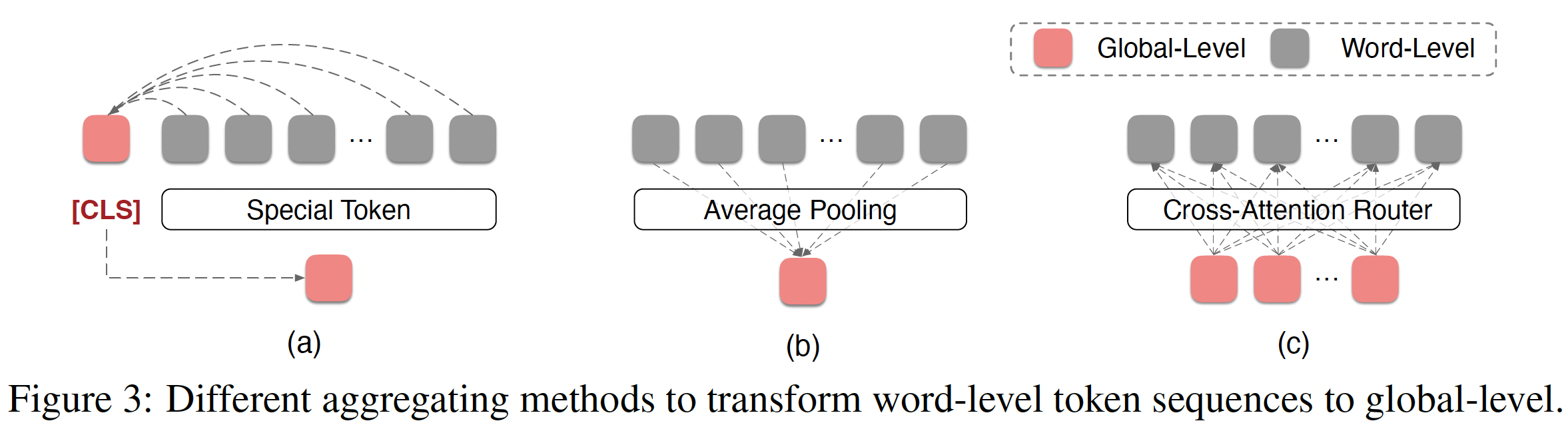
(3) Modality alignmnet module

\(\left\{\mathbf{h}_{\text {meta }, k}\right\}_{k=1}^M=\text { ModalAlign }\left(\left\{\widetilde{\mathbf{h}}_{\text {meta }, k}\right\}_{k=1}^M\right)\).

Summary

\[\left\{\mathbf{h}_{\text {meta }, k}\right\}_{k=1}^M=\operatorname{MetaEmbed}\left(\left\{\widehat{\mathbf{x}}_{\text {meta }, k}\right\}_{k=1}^M\right)\]

• Step 1) \(\left\{\widetilde{\mathbf{h}}_{\text {meta }, k}\right\}_{k=1}^M=\text { AvgPooling }\left(\text { LLMEncoder }\left(\left\{\widehat{\mathbf{x}}_{\text {meta }, k}\right\}_{k=1}^M\right)\right)\).

• Step 2) \(\left\{\mathbf{h}_{\text {meta }, k}\right\}_{k=1}^M=\text { ModalAlign }\left(\left\{\widetilde{\mathbf{h}}_{\text {meta }, k}\right\}_{k=1}^M\right)\).

(3) MetaTST

Endogenous + Exogenous + Metadata

a) Informative Embedding

Endogenous

• (1) Splits the endogenous series \(\mathbf{x}_{\text {en }}\) into \(N=\left\lfloor\frac{T_{\mathrm{en}}}{P}\right\rfloor\)
• (2) Linear projection: endogenous token \(\mathbf{h}_{\mathrm{en}, i}\)
  • with PatchEmbed \((\cdot): \mathbb{R}^P \rightarrow \mathbb{R}^D\).
• \(\left\{\mathbf{h}_{\mathrm{en}, i}\right\}_{i=1}^N=\operatorname{PatchEmbed}\left(\mathbf{x}_{\mathrm{en}}\right)\).

Exogenous

• Whole exogenous series \(\mathbf{x}_{\mathrm{ex}, j}\) into a \(D\)-dimensional exogenous token \(\mathbf{h}_{\mathrm{ex}, j}\).
• Variate-wise embedding SeriesEmbed \((\cdot): \mathbb{R}^{T_{\mathrm{cx}}} \rightarrow \mathbb{R}^D\)
• \(\left\{\mathbf{h}_{\mathrm{ex}, j}\right\}_{j=1}^C=\operatorname{SeriesEmbed}\left(\left\{\mathbf{x}_{\mathrm{ex}, j}\right\}_{j=1}^C\right)\).

Metadata token

• Have already been aligned to TS modality

Concatenation

• three types of tokens
• construct the informative embedding \(\mathbf{h}^0\), including
  • (1) \(N\) patch-wise endogenous tokens
  • (2) \(C\) series-wise exogenous tokens
  • (3) \(M\) metadata tokens
• \(\mathbf{h}^0=\operatorname{Concat}\left(\left\{\mathbf{h}_{\mathrm{en}, i}\right\}_{i=1}^N,\left\{\mathbf{h}_{\mathrm{ex}, j}\right\}_{j=1}^C,\left\{\mathbf{h}_{\mathrm{meta}, k}\right\}_{k=1}^M\right)\).

b) Informative Forecasting

\(\mathbf{h}^{l+1}=\operatorname{TransformerBlock}\left(\mathbf{h}^l\right), l \in\{1, \cdots, L\}\).

\(\widehat{\mathbf{y}}_{\mathrm{en}}=\text { Forecastor }\left(\mathbf{h}_{\mathrm{en}}^L\right)\).