Neural ODE
(1) Introduction
https://arxiv.org/abs/1806.07366
- 2018 NeurIPS Best paper
Contribution: Discrete layer \(\rightarrow\) Continuous layer
(2) 미분 & 적분
미분 & 적분
-
미분 = 기울기/변화율/도함수(dx)
-
적분 = 미분의 역 관계 ( = function approximation )
미분 방정식 (Differential Equation, DE)
- y를 x에 대해 미분한 “도함수를 포함”하는 방정식
두 종류의 DE
- (1) ODE (Ordinary DE, 상미분 방정식): univariate
- \(f^{\prime}(x)-2 x=0 \Leftrightarrow \frac{d f}{d x}-2 x=0 \Leftrightarrow y^{\prime}-2 x=0\).
- (2) PDE (Paratial DE, 편미분 방정식): multivariate
- \(\frac{\partial f(x, z)}{\partial x}+\frac{\partial f(x, z)}{\partial z}=0\).
(3) ODE
ODE를 푼다 = Function approximation
방정식 vs ODE
- 방정식을 푼다 = 해(= 값)을 찾는다
- ODE를 푼다 = 해(= 함수)을 찾는다
ODE를 어떻게 풀지? = 적분
- ex) Euler method
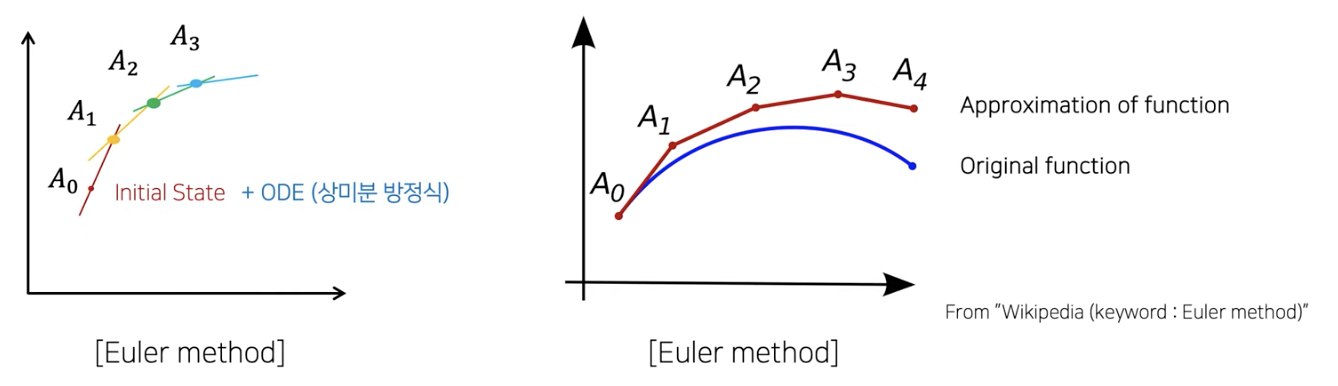
(4) Euler method
How? 무수한 더하기
두 가지가 필요함
- (1) Initial state
- (2) ODE
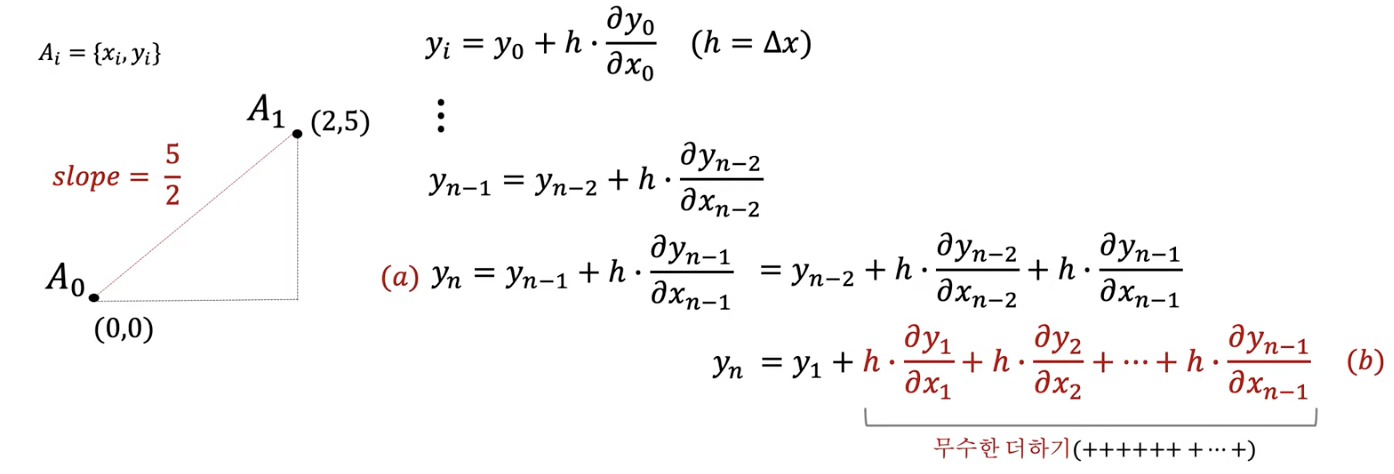
(5) Deep Learning
딥러닝의 최적화 = loss를 최소화하는 f(x) 찾기
= Function approximation
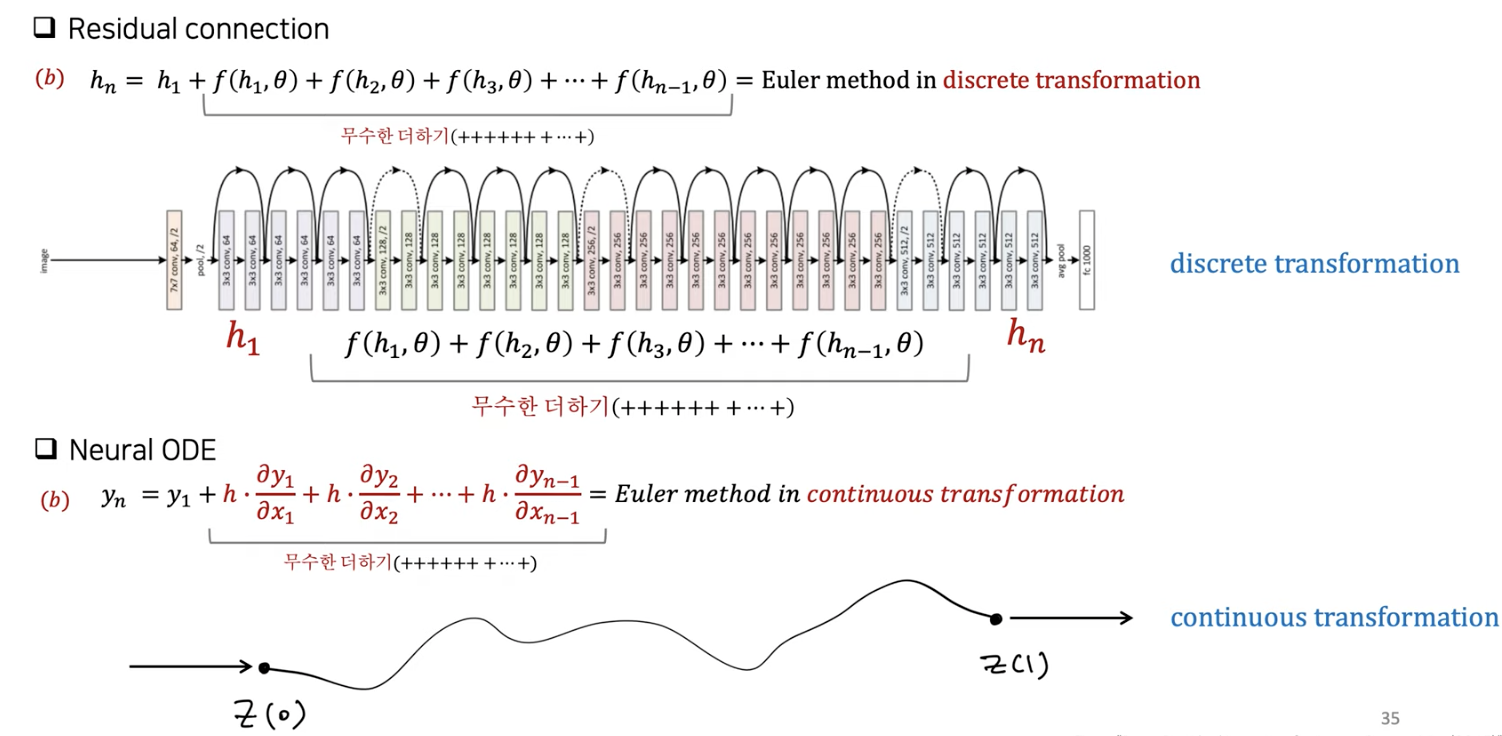
Residual connection vs. Neural ODE
- Residual connection:
- \(h_{t+1}=h_t+f\left(h_t, \theta\right)\).
- Neural ODE:
- \(y_n=y_1+h \cdot \frac{\partial y_1}{\partial x_1}+h \cdot \frac{\partial y_2}{\partial x_2}+\cdots+h \cdot \frac{\partial y_{n-1}}{\partial x_{n-1}}\).
(6) Residual connection vs. Neural ODE
a) Residual connection
\(h_{t+1}=h_t+f\left(h_t, \theta\right)\).
- \(h_2=h_1+f\left(h_1, \theta\right)\).
- \(h_3=h_2+f\left(h_2, \theta\right)=h_1+f\left(h_1, \theta\right)+f\left(h_2, \theta\right)\).
결론: \(h_n=h_1+f\left(h_1, \theta\right)+f\left(h_2, \theta\right)+f\left(h_3, \theta\right)+\cdots+f\left(h_{n-1}, \theta\right)\).
( = Euler method in discrete transformation )
b) Neural ODE
\(y_n=y_{n-1}+h \cdot \frac{\partial y_{n-1}}{\partial x_{n-1}}=y_{n-2}+h \cdot \frac{\partial y_{n-2}}{\partial x_{n-2}}+h \cdot \frac{\partial y_{n-1}}{\partial x_{n-1}}\).
결론: \(y_n=y_1+h \cdot \frac{\partial y_1}{\partial x_1}+h \cdot \frac{\partial y_2}{\partial x_2}+\cdots+h \cdot \frac{\partial y_{n-1}}{\partial x_{n-1}}\).
( = Euler method in continuous transformation )
(7) Neural ODE in SL
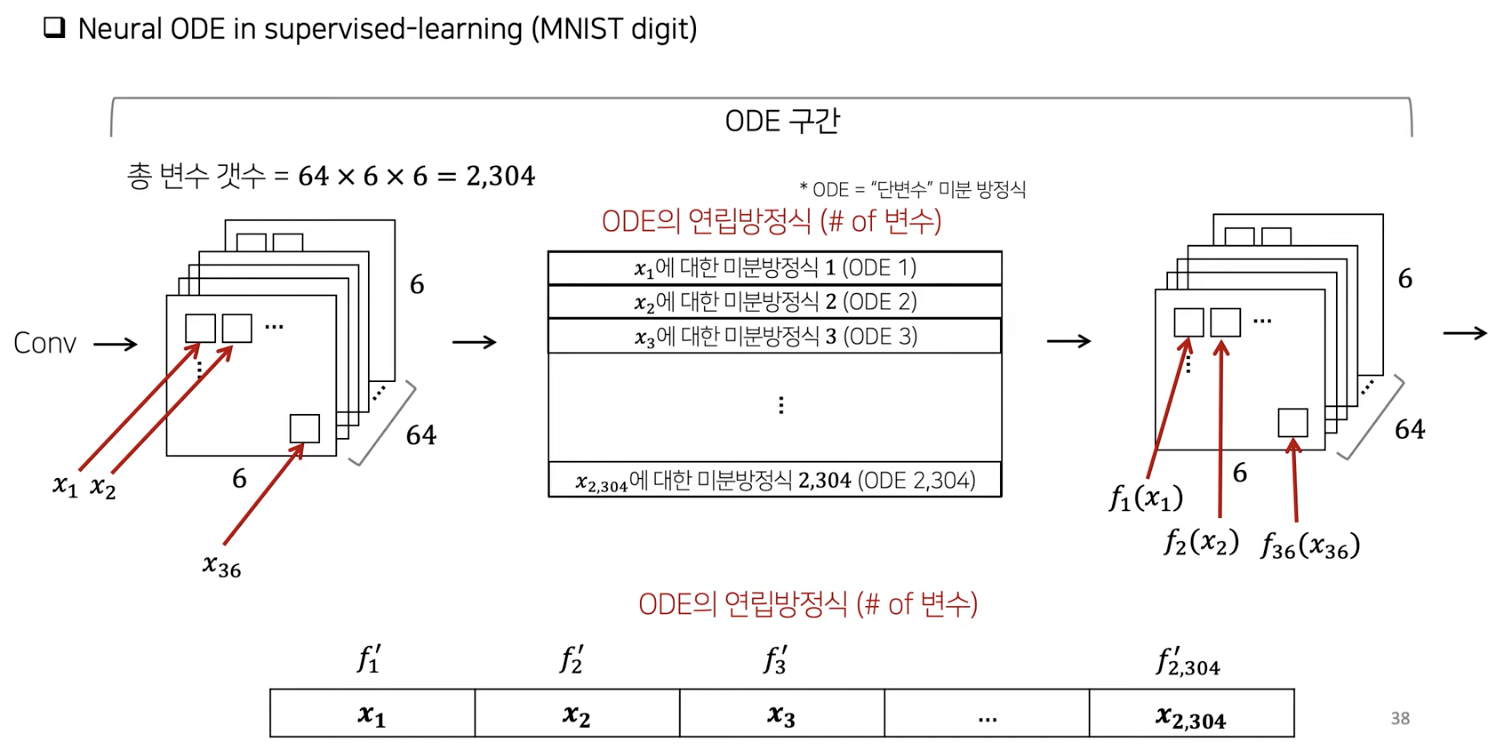
\(z(1)=z(0)+\int_0^1 f(z(t), t ; \theta) d t\).
- \(z\): ODE의 state (hidden vector)
- \(\int_0^1 f(z(t), t ; \theta) d t\) : \(z\)의 변화량
- 푸는 방법: Euler method
Forward & Backward
- Forward: Euler method
- Backward: Adjoint Sensitivity method
(8) Adjoint Sensitivity method
Procedure
-
(1) \(a(t)\) : adjoint state 정의
- 정의: 각 state 별 gradient
- 수식: \(a(t)=\frac{\partial \text { Loss }}{\partial z(t)}=\text { Gradient }=\text { Adjoint state of } ' t-\text { state }^{\prime}\)
-
(2) \(a(1) \rightarrow a(0)\).
-
\(a(0)\)을 얻기 위해서, 역으로 \(a(1)\)에서 시작하기!
( 새로운 ODE를 forward와 같은 방식으로 풀기 )
-
-
(3) \(a(\cdot)\) 를 통해 optimize 진행
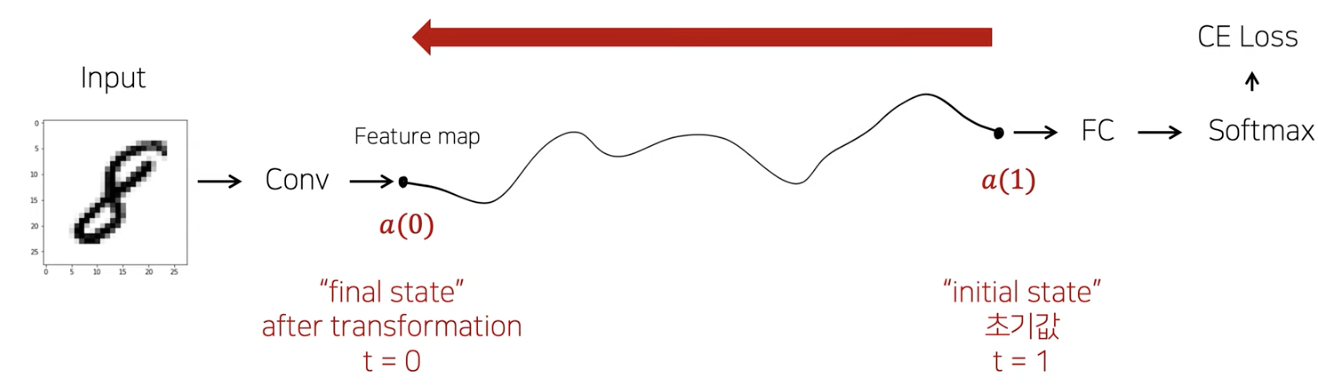
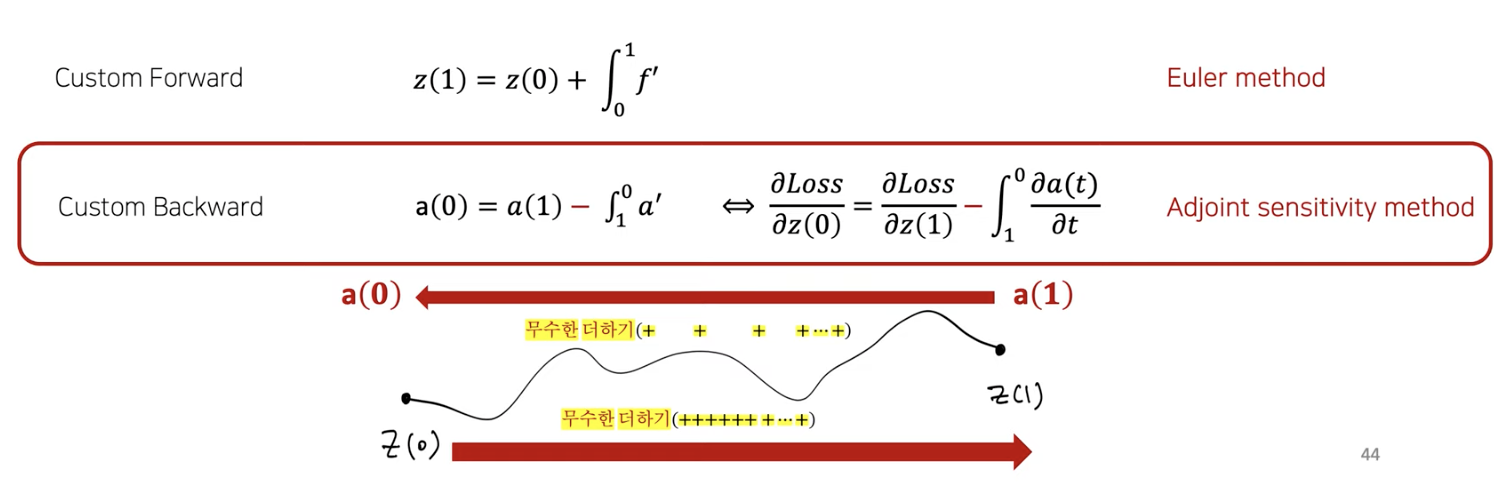
- 참고) \(\frac{d \mathbf{a}(t)}{d t}=-\mathbf{a}(t)^{\top} \frac{\partial f(\mathbf{z}(t), t, \theta)}{\partial \mathbf{z}}\).

Reference
https://www.youtube.com/watch?v=UegW1cIRee4
https://arxiv.org/abs/1806.07366
