(paper) Deep Transformer Models for Time Series Forecasting ; The Influenza Prevalence Case

Deep Transformer Models for Time Series Forecasting ; The Influenza Prevalence Case (2020, 97)

Contents

1. Abstract
2. Introduction
3. Background
   1. State Space Models (SSM)
4. Model
   1. Problem Definition
   2. Transformer Model
   3. Training

0. Abstract

Transformer-based model ( self-attention )

for UNIVARIATE & MULTIVARIATE TS

1. Introduction

Statistical & ML

• AR / ARMA / ARIMA

DL approaches

• CNN / RNN based
• Transformer architecture
  • does not process data in “ordered sequence manner”
  • have potential to model “complex dynamics of TS data”

Contributions

• 1) develop general Transformer-based model for TS forecasting
• 2) complementary to state space models
  • can also model “state variable” & “phase space”

2. Background

(1) State Space Models (SSM)

state & observable variables

• ex) generalized linear SSM
  • \(\begin{aligned} x_{t} &=Z_{t} \alpha_{t}+\epsilon_{t} \\ \alpha_{t+1} &=T_{t} \alpha_{t}+R_{t} \eta_{t}, t=1, \ldots, n, \end{aligned}\).

3. Model

(1) Problem Definition

\(N\) weekly data points : \(x_{t-N+1}, \ldots, x_{t-1}, x_{t}\)

• input : \(x_{t-N+1}, \ldots, x_{t-M}\)

• output : \(x_{t-M+1}, x_{t-M+2}, \ldots, x_{t}\)

• each data point \(x_t\) : scalar / vector ( univariate / multivariate )

(2) Transformer Model

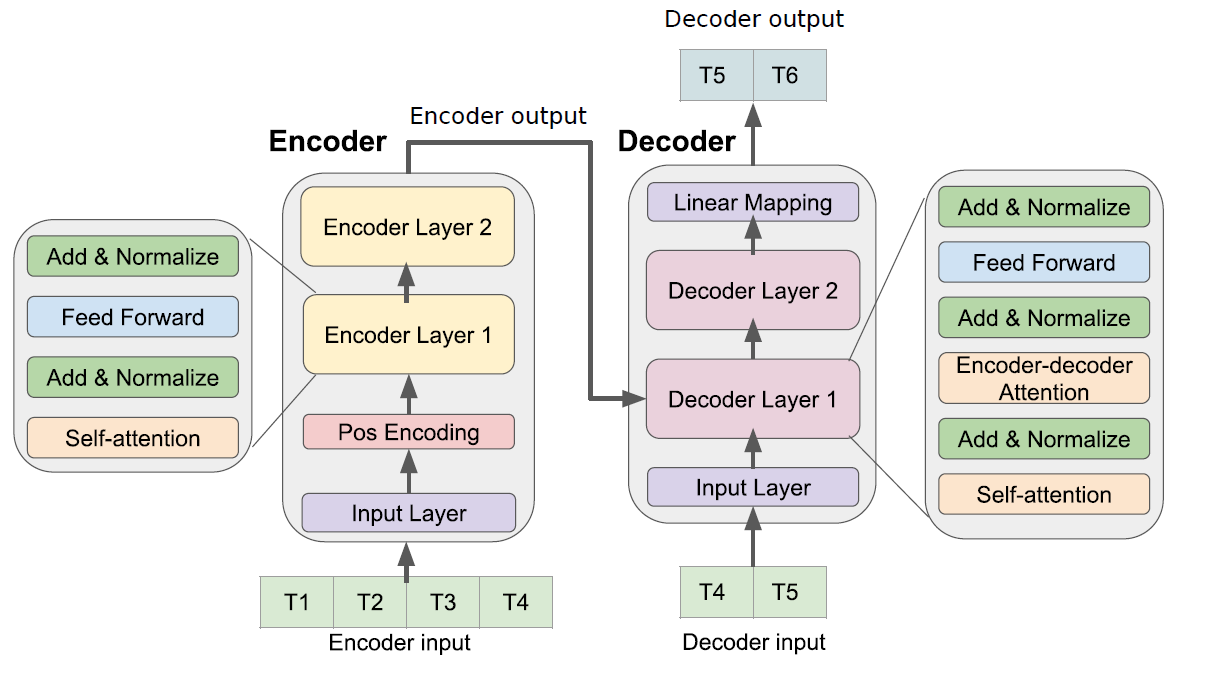
(3) Training

train the model…

• to predict 4 future
• with 10 data points

That is..

• encoder input : \(\left(x_{1}, x_{2}, \ldots, x_{10}\right)\)
• decoder input : \(\left(x_{10}, \ldots, x_{13}\right)\)
• decoder output aims : \(\left(x_{11}, \ldots, x_{14}\right)\)