(paper) Deep and Confident Prediction for Time Series at Uber

Deep and Confident Prediction for Time Series at Uber (2017, 270)

Contents

1. Abstract
2. Introduction
3. Related Works
   1. BNN
4. Method
   1. Prediction Uncertainty
5. Model Design

0. Abstract

“Uncertainty Estimation” using probabilistic TS forecasting

• propose a novel end-to-end Bayesian Deep Model

1. Introduction

prediction uncertainty can be decomposed into….

• 1) model uncertainty ( = epsitemic uncertainty )
  • captures ignorance of model parameters
  • can be reduced with more samples
• 2) inherent noise
  • irreducible
• 3) model misspecification
  • test sample from different population

\(\rightarrow\) propose a principled solution to incorporate this uncertainty

( using encoder-decoder framework )

2. Related Works

(1) BNN

find the posterior disn of \(W\)

• exact posterior inference is rarely available

  \(\rightarrow\) use approximate Bayesian Inference

How about, without changing NN architecture?

\(\rightarrow\) MC Dropout

• easy to implement!

3. Method

Trained NN : \(f^{\hat{W}}(\cdot)\)

Goal : evaluate the UNCERTAINTY of the model prediction ( = \(\hat{y}^{*}=f^{\hat{W}}\left(x^{*}\right)\) )

• quantify the prediction standard error \(\eta\),

  so that \(\alpha\)-level prediction interval be \(\left[\hat{y}^{*}-z_{\alpha / 2} \eta, \hat{y}^{*}+z_{\alpha / 2} \eta\right]\)

(1) Prediction Uncertainty

Gaussian Prior : \(W \sim N(0, I)\)

Model : \(y \mid W \sim N\left(f^{W}(x), \sigma^{2}\right)\).

Variance of the prediction distn :

\(\begin{aligned} \operatorname{Var}\left(y^{*} \mid x^{*}\right) &=\operatorname{Var}\left[\mathbb{E}\left(y^{*} \mid W, x^{*}\right)\right]+\mathbb{E}\left[\operatorname{Var}\left(y^{*} \mid W, x^{*}\right)\right] \\ &=\operatorname{Var}\left(f^{W}\left(x^{*}\right)\right)+\sigma^{2} \end{aligned}\).

• term 1 : \(\operatorname{Var}\left(f^{W}\left(x^{*}\right)\right)\)
  • model uncertainty
• term 2 : \(\sigma^{2}\)
  • inherent noise
• underlying assumption :
  • \(y^{*}\) is generated by the same procedure

Therefore, propose with “3 sources”

• 1) model uncertainty
• 2) model misspecification
• 3) inherent noise level

(a) Model Uncertainty

• posterior distn \(p(W \mid X, Y)\)

• use MC dropout to estimate model uncertainty

  \(\rightarrow\) approximate it with “sample variance”

  \(\widehat{\operatorname{Var}}\left(f^{W}\left(x^{*}\right)\right)=\frac{1}{B} \sum_{b=1}^{B}\left(\hat{y}_{(b)}^{*}-\overline{\hat{y}}^{*}\right)^{2}\).

  • where \(\overline{\hat{y}}^{*}=\frac{1}{B} \sum_{b=1}^{B} \hat{y}_{(b)}^{*}\)
  • repeat prediction \(B\) times ( \(\left\{\hat{y}_{(1)}^{*}, \ldots, \hat{y}_{(B)}^{*}\right\}\) )

• choose optimal dropout probability \(p\) adaptively

  ( treat it as a model parameter )

(b) Model Misspecification

• capture potential model misspecification
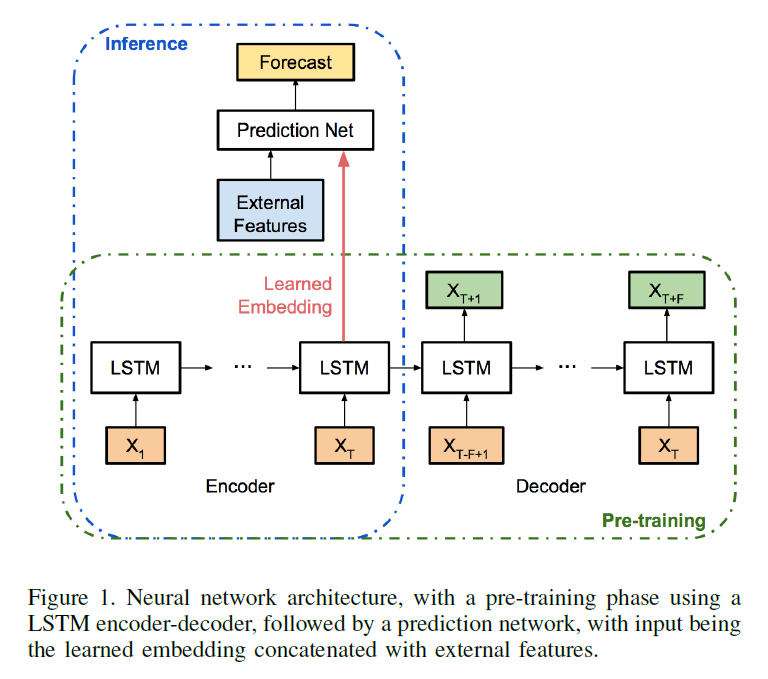
• by introducing “encoder-decoder” frameowork
• Step
  • step 1) train an ENCODER ( \(g(\cdot)\) )
  • step 2) reconstruct with DECODER ( \(h(\cdot)\) )
• treat them as one large network ( \(f=h(g(\cdot))\) )

(c) Inherent noise

• estimate \(\sigma^2\)

• (original MC dropout) implicitly determined by prior over smoothness of \(W\)

• (proposal)

  • simple & adaptive approach

  • estimate the noise level via “the residual sum of squares”,

    evaluated on an independent held-out validation set

• Notation

  • \(f^{\hat{W}}(\cdot)\) : fitted model on “training data”
  • \(X^{\prime}=\left\{x_{1}^{\prime}, \ldots, x_{V}^{\prime}\right\}, Y^{\prime}=\left\{y_{1}^{\prime}, \ldots, y_{V}^{\prime}\right\}\) : independent validation set
  • estimate \(\hat{\sigma}^{2}=\frac{1}{V} \sum_{v=1}^{V}\left(y_{v}^{\prime}-f^{\hat{W}}\left(x_{v}^{\prime}\right)\right)^{2}\)
    • asymptotically unbiased estimation of true model!

(2) Model Design

2 components

• 1) encoder-decoder
• 2) prediction network

(a) encoder-decoder

• encoder input : \(\left\{x_{1}, \ldots, x_{T}\right\}\)
• decoder input : \(\left\{x_{T-F+1}, \ldots, x_{T}\right\}\)
• decoder output : \(\left\{x_{T+1}, \ldots, x_{T+F}\right\}\)

(b) prediction network

After ‘encoder-decoder’ is pre-trained!

use MLP

(c) Inference

after full model is trained, make inference!

\(\eta\) contains 2 terms

• 1) model uncertainty

• 2) misspecification uncertainty

  ( both estimated by MC dropout )

with held-out validation set,

• 3) inherent noise level

2 hyperparameters

• 1) dropout probability, \(p\)
• 2) number of iterations, \(B\)