(paper) Adversarial Examples in Deep Learning for Multivariate Time Series Regression

Adversarial Examples in Deep Learning for Multivariate Time Series Regression (2020,9)

Contents

1. Abstract
2. Introduction
3. Adversarial Examples for MTS
   1. Formalization of MTS regression
   2. FGSM & BIM

0. Abstract

Adversarial attacks

• DL algorithm : susceptibility to adversarial attacks
• no previous works related to TS

Craft adversarial MTS examples for 3 models

• CNN/LSTM/GRU

Test on..

• Google Stock & Household Power consumption dataset

1. Introduction

DL models can be easily fooled!

• by making small perturbations

Adversarial attacks

• usually in image recognition & classification
• but, not much on non-image task

This paper

• apply & transfer “adversarial attacks” from image domain

  to DL regression models for “MTL forecasting”

Main contributions

• 1) formalize adversarial attacks
• 2) crafting adversarial attacks for MTL using CNN/LSTM/GRU
• 3) study on 2 datasets
  • data 1) finance
  • data 2) energy domain

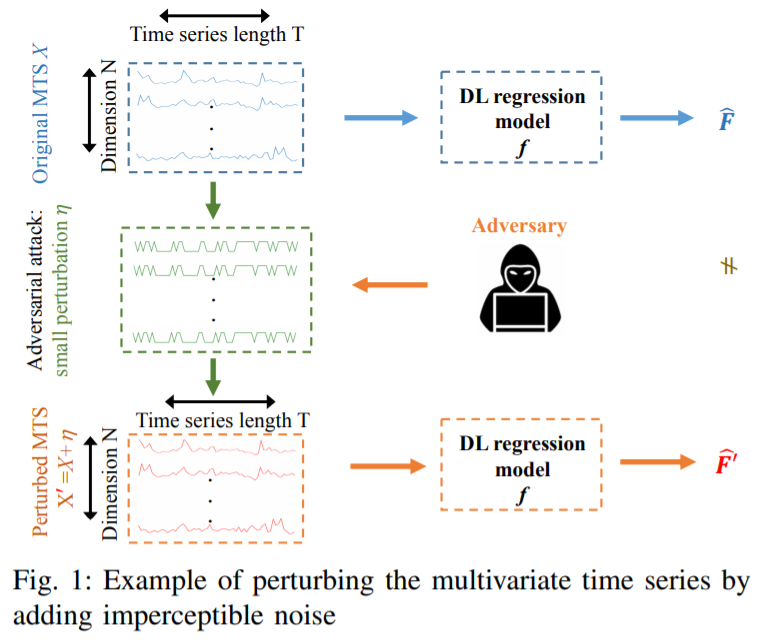
2. Adversarial Examples for MTS

(1) Formalization of MTS regression

\(X=\left[x_{1}, x_{2}, \ldots, x_{T}\right]\).

• \(T=\mid X\mid\) : length of \(X\)
• \(x_{i} \in \mathbb{R}^{N}\) :
  • time : \(i\) , where \(i \in[1, T]\).
  • # of dimension : \(N\)

\(D=\left(x_{1}, F_{1}\right),\left(x_{2}, F_{2}\right), \ldots,\left(x_{T}, F_{T}\right)\).

• data set of pair \(\left(x_{i}, F_{i}\right)\)
• \(F_i\) : label of \(x_i\)

\(X^{'}\) : adversarial example ( perturbed \(X\) )

• \(\hat{F} \neq \hat{F}^{\prime}\) & \(\mid \mid X-X^{\prime} \mid \mid \leq \epsilon\)

Regression Task & Cost function

• [regression] \(f(\cdot): \mathbb{R}^{N \times T} \rightarrow \hat{F}\).
• [cost function] \(J_{f}(\cdot, \cdot)\)

Box-constrained optimization problem

\(\begin{gathered} \min _{X^{\prime}} \mid \mid X^{\prime}-X \mid \mid \text { s.t. } \\ f\left(X^{\prime}\right)=\hat{F}^{\prime}, f(X)=\hat{F} \text { and } \hat{F} \neq \hat{F}^{\prime} \end{gathered}\).

(2) FGSM & BIM

FGSM (Fast Gradient Sign Method)

BIM (Basic Iterative Method)

• extension of FGSM

• BIM = FGSM x multiple times

  • with small step size

  • clipping after each step

    ( to ensure to become inside the range \([X-\epsilon, X+\epsilon]\) )