TCN for Anomaly Detection in TS (2019,34)
Contents
- Abstract
- Introduction
- Convolutional Sequence Model
- TCN
- Dilated Convolutions
- Residual Connections
- Multi-scale Feature Maps for Prediction
- Anomaly Detection
Abstract
TCN = causal convolutions & dilations
\(\rightarrow\) apply TCN for “anomaly detection”
Steps
-
1) apply TCN to predict trend
-
2) prediction errors are fitted by Multivariate Gaussian distribution &
used to calculate the anomaly scores
1. Introduction
propose anomaly detection algorithm in unsupervised way
- 1) TCN : predictor model
- 2) Multivariate Gaussian : identify anomaly points in TS
2. Convolutional Sequence Model
Notation
- \(X\) : time series
- \(x_{t} \in R^{m}\) : each time point
Prediction model
- predict next \(l\) values, with window of length \(L\)
Residuals between
- 1) prediction values
- 2) real values
are calculated & fit a Multivariate Gaussian distribution model
(1) TCN
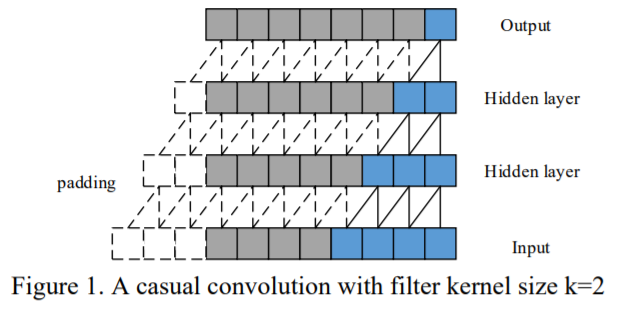
2 constraints
- 1) output of the network should have the same length as input
- 2) can only use information of past time steps
\(\rightarrow\) zero padding & no cheating
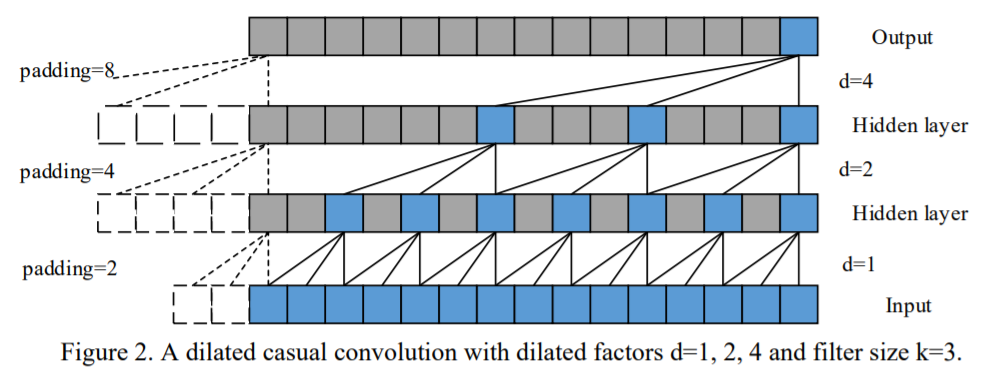
(2) Dilated Convolutions
to memorize LONG term
( should make larger receptive field)
(3) Residual Connections
- pass
(4) Multi-scale Feature Maps for Prediction
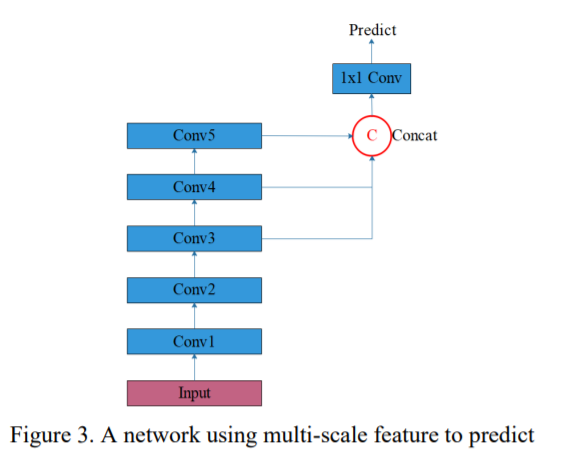
to capture different scale patterns
- not only one last layer,
- but also use multiple layers!
3. Anomaly Detection
implemented in point-wise
prediction errors distribution on training data, is modeled with Multivariate Gaussian
Anomaly score :
- \(e_t\) : observation prediction error
\(\rightarrow\) \(x^{(t)}\) is classified as “anomalous”, if \(a_t > \tau\)
