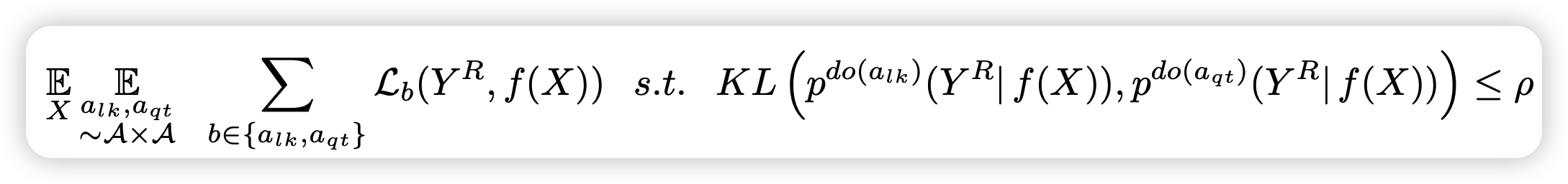Representation Learning via Invariant Causal Mechanisms (2020, 47)
Contents
- Abstract
- Introduction
- Representation Learning via Invariant Causal Mechanisms
- Problem Setting
- Causal Interpretation
- ReLIC objective
0. Abstract
idea : self-supervised representation using a causal framework
- show how data augmentations can be effectilvey utilized, through explicit invariance constraints
\(\rightarrow\) propose a novel self-supervised objective, ReLIC
ReLIC
= Representation Learning via Invariant Causal Mechanism
\(\rightarrow\) enforce invariant prediction of proxy targets … improved generalization!
1. Introduction
data generating process using a CAUSAL graph
& leverage causal tools to derive properties of the optimal representation
Representatin should be an invariant predictor of proxy targets
( not causally related to the downstream targets of interest )
(1) Use data augmentations to simulate a subset of possible interventions
(2) Propose a regularizer, which enforces that the prediction of the proxy targets is invariant across data uagmentations
Contributions
-
(1) formalize problem of self-supervised representation learning using causality
& propose to more effectively learning data augmentations through invariant prediction
-
(2) propose ReLIC
- enforces invariant prediction through explicit regularizer
2. Representation Learning via Invariant Causal Mechanisms
(1) Problem Setting
Notation
-
\(X\) : unlabelled observed data
-
\(\mathcal{Y}=\left\{Y_{t}\right\}_{t=1}^{T}\) : set of unknown tasks
-
\(Y_{t}\) : targets for task \(t\)
-
\(\left\{Y_{t}\right\}_{t=1}^{T}\) : multi-task setup
-
Goal
-
PRE-train with UNsupervised data a representation \(f(X)\) ,
that will be useful for solving downstream tasks \(\mathcal{Y}\)
(2) Causal Interpretation
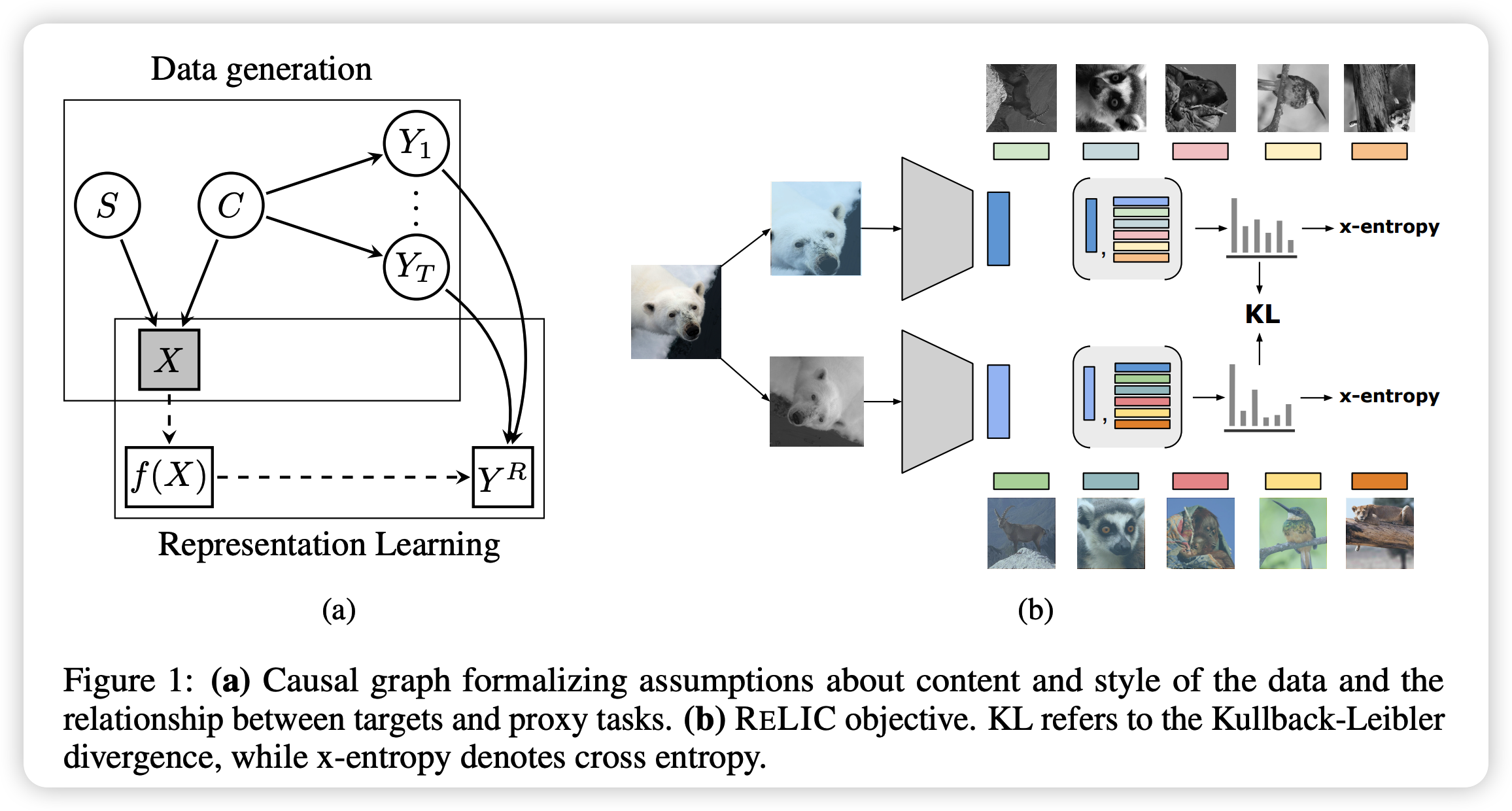
Assumptioin
- (1) data is generated from CONTENT & STYLE variables
- (2) only CONTENT being relevant for unknown downstream tasks
- (3) CONTENT & STYLE are independent
Content
- good representation of the data for downstream taks
- goal of representation learning = estimating content
Notation
- \(C\) : latent variable describing CONTENT
- \(S\) : latent variable describing STYLE
Independence of mechanisms
- intervention of \(S\) does not change \(P(Y_t \mid C)\)
- that is…
- \(p^{d o\left(S=s_{i}\right)}\left(Y_{t} \mid C\right)=p^{d o\left(S=s_{j}\right)}\left(Y_{t} \mid C\right) \quad \forall s_{i}, s_{j} \in \mathcal{S}\).
(1) Since the targets \(Y_t\) are unknown, construct a proxy task \(Y^T\) to learn representation
(2) To learn INVARIANT representation, enforce above equation!
- since no access to \(S\) …. use content-preserving data augmentations
- ex) rotation, gray-scaling, translation, cropping …
(3) ReLIC objective
goal : prediction of proxy targets from the representation is INVARIANT under data augmentations
-
invariant prediction criteria =
\(p^{\mathrm{do}\left(a_{i}\right)}\left(Y^{R} \mid f(X)\right)=p^{\mathrm{do}\left(a_{j}\right)}\left(Y^{R} \mid f(X)\right) \quad \forall a_{i}, a_{j} \in \mathcal{A}\).
- \(\mathcal{A}=\left\{a_{1}, \ldots, a_{m}\right\}\) is the set of data augmentations
-
enforce this through regularizer