(paper) Time Series is a Special Sequence ; Forecasting with Sample Convolution and Interaction

Time Series is a Special Sequence : Forecasting with Sample Convolution and Interaction (2021)

Contents

1. Abstract
2. Introduction
3. Related Work & Motivation
   1. Related Work
   2. Rethinking “Dilated Causal Convolution”
4. SCINet : Sample Convolution & Interaction Networks

0. Abstract

3 components in TS

• 1) trend
• 2) seasonality
• 3) irregular components

propose SCINet

• conducts sample convolution & interaction for temporal modeling
• enables multi-resolution analysis

1. Introduction

TSF (Time Series Forecasting)

Traditional TSF

• ARIMA, Holt-Winters

  \(\rightarrow\) mainly applicable to “univariate” TSF

TSF using DNNs

• 1) RNNs
• 2) Transformer
• 3) TCN (Temporal Convolutional Networks)
  • most effective & efficient
  • combined with GNNs

\(\rightarrow\) ignore the fact that TS is a special “SEQUENCE data”

SCINet

contribution

• 1) propose a hierarchical TSF framework
  • iteratively extract & exchange information, at “different temporal resolutions”
• 2) basic building block : SCI-Block
  • down samples input data into 2 sub-sequence
  • extract features of each sub-sequence ( using distinct filters )

2. Related Work & Motivation

Notation

• \(\mathbf{X}^{*}\): long time series
• \(T\) : look-back window
• goal :
  • predict \(\hat{\mathbf{X}}_{t+1: t+\tau}=\left\{\mathrm{x}_{t+1}, \ldots, \mathrm{x}_{t+\tau}\right\}\)
  • given \(\mathbf{X}_{t-T+1: t}=\left\{\mathbf{x}_{t-T+1}, \ldots, \mathbf{x}_{t}\right\}\)
• \(\tau\) : forecast horizon
• \[\mathrm{x}_{t} \in \mathbb{R}^{d}\]
  • \(d\) : # of variates
• omit subscripts! will use \(\mathbf{X}\) and \(\hat{\mathbf{X}}\)

Multi-step forecasting ( \(\tau >1\) )

• 1) DMS ( DIRECT multi-step ) estimation
• 2) IMS ( ITERATED multi-step ) estimation

(1) Related Work

RNN based

• use internal memory state
• generally belong to IMS
  • suffer from error accumulation
• gradient vanishing/exploding

Transformer

• self attention mechanism
• problem : overhead of Transformer-based models!

Convolution based

• capture local correlation of TS
• SCINet is constructed based on TEMPORAL convolution

(2) Rethinking “Dilated Causal Convolution”

Temporal Convolutional Networks

• stack of causal convolutions ( to prevent information leakage )

  with exponentially enlarge dilation factors ( for large receptive field with few layers )

Causality should be kept!

• “future information leakage” problem exists, only when the output & input have temporal overlaps
• that is, “causal convolutions” should be applied only in “IMS-based forecasting”

propose a novel “downsample-convolve-interact architecture”, SCINet

3. SCINet : Sample Convolution & Interaction Networks

Key points

• “Hierarchical” framework
• capture “temporal dependencies” at multiple-temporal resolutions
• basic building block = “SCI-Block”
  • 1) down sample input data into 2 parts
  • 2) distinct filters for 2 parts ( extract both homo/heterogeneous information )
  • 3) incorporate “interactive learning”
• SCINet = multiple SCI-Blocks into a “binary tree” structure
• concatenate all low-resolution components into new seqeunce

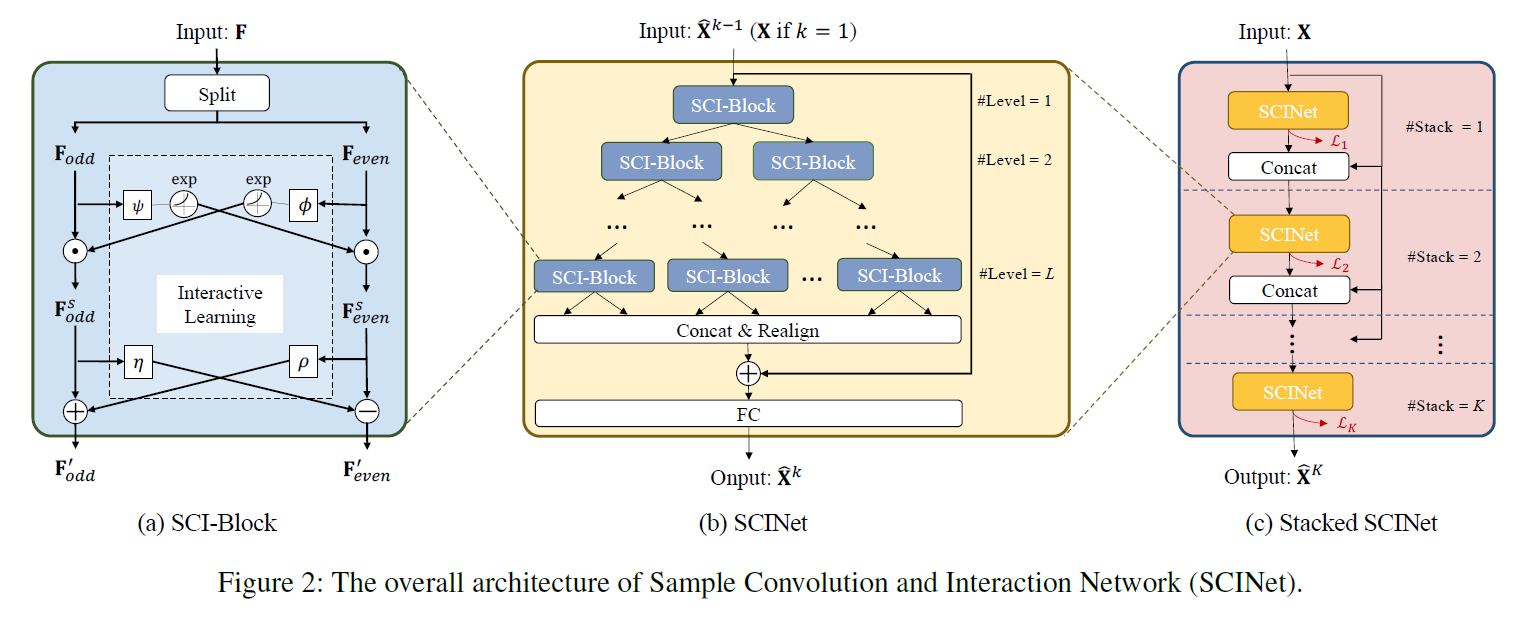
(1) SCI-Block

abstract

• [ input ] feature \(\mathbf{F}\)

• [ output ] sub-features \(\mathbf{F}_{\text {odd }}^{\prime}\) and \(\mathbf{F}_{\text {even }}^{\prime}\)
• [ method ] by “Splitting” & “Interactive Learning”

Step 1) split

Step 2) different kernels

• extracted features would contain “homo” & “hetero”geneous information
  • 2 different 1D CNN ( \(\phi\) , \(\psi\) )

Step 3) Interactive learning

• allow information interchange
• \(\begin{gathered} \mathbf{F}_{\text {odd }}^{s}=\mathbf{F}_{\text {odd }} \odot \exp \left(\phi\left(\mathbf{F}_{\text {even }}\right)\right), \quad \mathbf{F}_{\text {even }}^{s}=\mathbf{F}_{\text {even }} \odot \exp \left(\psi\left(\mathbf{F}_{\text {odd }}\right)\right) . \\ \mathbf{F}_{\text {odd }}^{\prime}=\mathbf{F}_{\text {odd }}^{s} \pm \rho\left(\mathbf{F}_{\text {even }}^{s}\right), \quad \mathbf{F}_{\text {even }}^{\prime}=\mathbf{F}_{\text {even }}^{s} \pm \eta\left(\mathbf{F}_{\text {odd }}^{s}\right) . \end{gathered}\).

Proposed downsample-convolve-interact architecture achieves larger receptive field

Unlike TCN that employs a “single shared convolutional filter” in each layer,

SCI-Block aggregates essential information extracted from the 2 downsampled sub-sequences

(2) SCINet

• multiple SCI-Blocs hierarchically!

• \(2^l\) SCI-blocks at \(l\)-th level

  • \(l\) = \(1 \cdots L\)
  • input for \(k\)-th SCINet : \(\hat{\mathbf{X}}^{k-1}=\left\{\hat{\mathbf{x}}_{1}^{k-1}, \ldots, \hat{\mathbf{x}}_{\tau}^{k-1}\right\}\)
    • gradually down-sampled!

• information from previous levels will be accumulated

  \(\rightarrow\) capture both SHORT & LONG TERM dependencies

• FC layer to decode

(3) Stacked SCINet

• stack \(K\) layers of SCINets
• apply “intermediate supervision”

(4) Loss Function

\(\mathcal{L}=\sum_{k=1}^{K} \mathcal{L}_{k}\).

• \(\mathcal{L}_{k}=\frac{1}{\tau} \sum_{i=0}^{\tau} \mid \mid \hat{\mathrm{x}}_{i}^{k}-\mathrm{x}_{i} \mid \mid\).

Experiment dataset :

• Electricity Transformer Temperature
• traffic datasets PeMS

4. Limitation & Future Work

1) TS might contain noisy data / missing data / collected at irregular time intervals

\(\rightarrow\) proposed downsampling method may have difficulty dealing with “IRREGULAR intervals”

2) extend to “PROBABILISTIC” forecast

3) without modeling “SPATIAL relations”