( 참고 : Fast Campus 금융공학/퀀트 강의 )
4. 시계열 회귀분석
(1) 회귀 분석
- 생략
(2) 잔차 분석
Durbin-Watson Test
- 회귀 모형의 잔차가 white noise인지 test
library(lmtest)
dwtest(sales_lm)
잔차에 autocorrelation이 존재하는지 확인해서,
만약 존재한다면 “추가적인 모형으로 더 설명”할 여지가 있음
이러한 경우, AR(1)등의 모형을 추가적으로 사용!
즉, 시계열 회귀분석은
- 1) “선형 회귀 모형”으로 1차 모델링
- 2) 남은 잔차를 “시계열 모형”으로 한번 더 모델링
( 실제로는 이것을 2 step으로 하지 않고, 한번에 파라미터를 추정함 )
covariates = c("Open", "Promo", "SchoolHoliday")
model = auto.arima(sales_train[,"Sales"],
xreg = sales_train[, covariates])
sales_forecast = forecast(model,
xreg = sales_test[, covariates])
(3) 시계열의 다중 계절성 & TBATS
MSTS
하나의 데이터가 “하나의 주기가 아닌 여러 개의 주기”가 있을 경우?
- case1 ) 주별
- case 2) 주별 & 연별
city_ts = ts(city_train, frequency = 7)
city_msts = msts(city_train, seasonal.periods = c(7,365.25))
TBATS model
-
시계열을 Box-cox transformation으로 변환
( 분산을 일정하게 해줌 )
-
Exponential Smoothing으로 Trend 추정
-
Error를 ARMA 모형으로 모델링
-
Multi-seasonality를 Fourier Series를 사용하여 추출
city_msts = msts(city_train, seasonal.periods = c(7, 365))
tbats_msts = tbats(city_msts)
fcst_msts = forecast(tbats_msts, h = 365)
Fourier Series (푸리에 급수)?
- 주기 함수를 “삼각함수의 가중치”로 분해
- ex) seasonality를 sine & cosine 사용하여 표현
\(\begin{aligned} g(t) &=a_{0}+\sum_{m=1}^{\infty} a_{m} \cos \left(\frac{2 \pi m t}{T}\right)+\sum_{n=1}^{\infty} b_{n} \sin \left(\frac{2 \pi n t}{T}\right) \\ &=\sum_{m=0}^{\infty} a_{m} \cos \left(\frac{2 \pi m t}{T}\right)+\sum_{n=1}^{\infty} b_{n} \sin \left(\frac{2 \pi n t}{T}\right) \end{aligned}\).
[ 계절성 = sine & cosine의 weighted sum ]
\(y_{t}=a+\sum_{k=1}^{K}\left[\alpha_{k} \sin (2 \pi k t / m)+\beta_{k} \cos (2 \pi k t / m)\right]+N_{t}\).
- \(N_t\) : ARIMA 모형
- \(m\) : 주기(frequency)
- \(K\) : seasonal/smoothing 파라미터
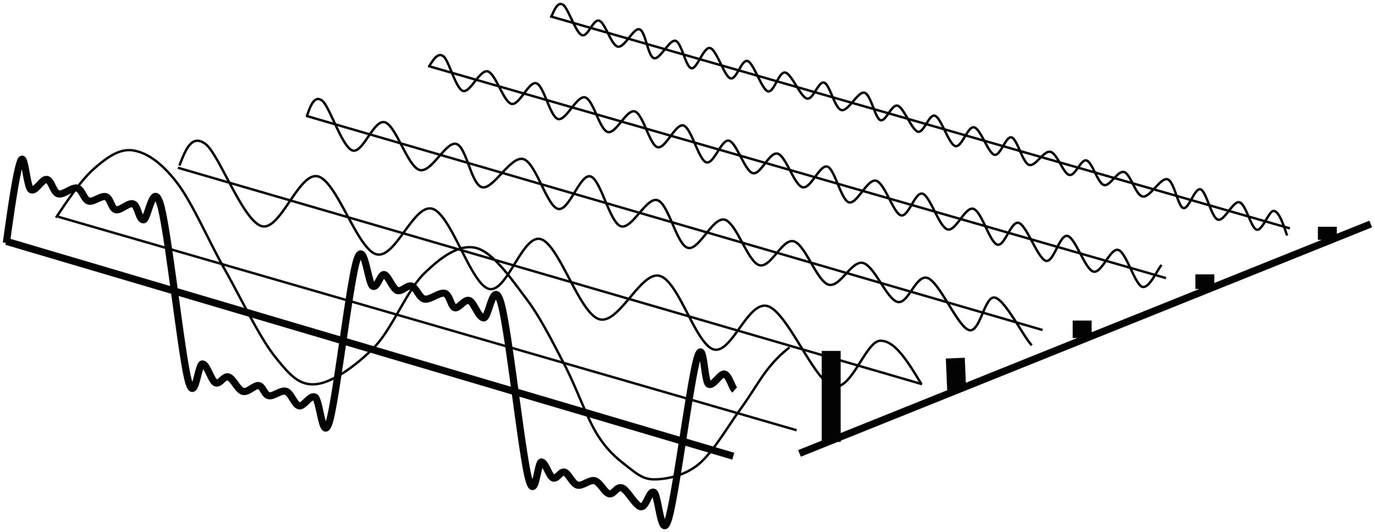
# 1) 단일 계절성 (7)
city_ts = ts(city_train, frequency = 7)
# 2) 이중 계절성 (7 & 365)
city_msts = msts(city_train, seasonal.periods = c(7, 365))
# 3) 삼중 계절성 (7 & 30 & 365)
city_msts2 = msts(city_train, seasonal.periods = c(7, 30, 365))
arima in R
-
frequency 최대 350 & 다중 계절성 (X)
\(\rightarrow\) fourier series를 이용해야!
-
auto.arima는 , 내부적으로 fourier term을 추가하여 seasonality 계산
# 1) Time Series
city_msts = msts(city, seasonal.periods = c(7, 365))
# 2) Fourier Series
z = fourier(city_msts, K = c(3, 10)) # for train
zreg = fourier(city_msts, K = c(3, 10), h = 365) # for test (미래)
# 3) MODEL( Time SEries, Fourier Series)
model = auto.arima(city_msts, seasonal = FALSE, xreg = z)
# 4) ForeCast
forecast(model, xreg = zreg, h = 365)
