1. 데이터 관점의 분류
- 횡단면 데이터 (Cross Sectional)
- 시계열 데이터 (Time Series)
- 시계열 횡단면 데이터 (Pooled Cross Sectional)
- 패널 데이터 (Panel Data)
| ’ | 횡단면 데이터 | 시계열 데이터 | 시계열 횡단면 데이터 | 패널 데이터 |
|---|---|---|---|---|
| 정의 | 특정시점 + 다수독립변수 | 다수시점 + 특정독립변수 | 다수독립변수 + 다수시점 | 다수독립변수 + 다수시점 (동일 변수 및 시점) |
| 예시 | 2016년 16개 시도의 GRDP와 최종소비 | 연도별 전국 GRDP와 최종소비 | 연도별 16개 시도의 GRDP와 최종소비 | 연도별 16개 시도의 GRDP와 최종소비 |
| 특징 | 값 독립적, 모집단 중 특정 시점 표본추출 | 값 Serial-correlation/Trend/Seasonality 등 | 시점/변수 불일치로 공백 가능 | 시점/변수 일치로 연구자들이 가장 선호 |
2. 시계열 데이터
확률 과정(Stochastic Process): “상관 관계”를 가지는 무한개의 변수의 순서열
\(Y\) = {\(\dots\), \(Y_{-2}\), \(Y_{-1}\), \(Y_{0}\), \(Y_{1}\), \(Y_{2}\), \(\dots\)}
\(X\) = {\(\dots\), \(X_{-2}\), \(X_{-1}\), \(X_{0}\), \(X_{1}\), \(X_{2}\), \(\dots\)}
-
….
- \(X_1\) = {\(\dots\), \(X_{1,-2}\), \(X_{1,-1}\), \(X_{1,0}\), \(X_{1,1}\), \(X_{1,2}\), \(\dots\)}
- \(X_2\) = {\(\dots\), \(X_{2,-2}\), \(X_{2,-1}\), \(X_{2,0}\), \(X_{2,1}\), \(X_{2,2}\), \(\dots\)}
- ….
시계열 데이터(Time Series Data)
-
독립변수(\(x_t\)) & 종속변수(\(y_t\))가 시간 단위(\(t\))를 포함
- \(y\) = {\(\dots\), \(y_{-2}\), \(y_{-1}\), \(y_{0}\), \(y_{1}\), \(y_{2}\), \(\dots\)} ( = \(\{y_t\}_{-\infty}^{\infty}\) )
- \(x\) = {\(\dots\), \(x_{-2}\), \(x_{-1}\), \(x_{0}\), \(x_{1}\), \(x_{2}\), \(\dots\)} ( = \(\{x_t\}_{-\infty}^{\infty}\))
- ….
- \(x_1\) = {\(\dots\), \(x_{1,-2}\), \(x_{1,-1}\), \(x_{1,0}\), \(x_{1,1}\), \(x_{1,2}\), \(\dots\)}
- ….
- TSF의 예측값 : \(y\)의 시간 \(t\)에서의 예측값(\(\hat{y_t}\))
3. Feature Extraction (=FE)
(1) 빈도 (Frequencey)
- 정의 : 계절성 패턴(Seasonality)이 나타나기 전까지의 데이터 개수
- example ) 계설성이 1년에 1회 나타날 경우,
| Data | frequency |
|---|---|
| Annual | 1 |
| Quarterly | 4 |
| Monthly | 12 |
| Weekly | 52 |
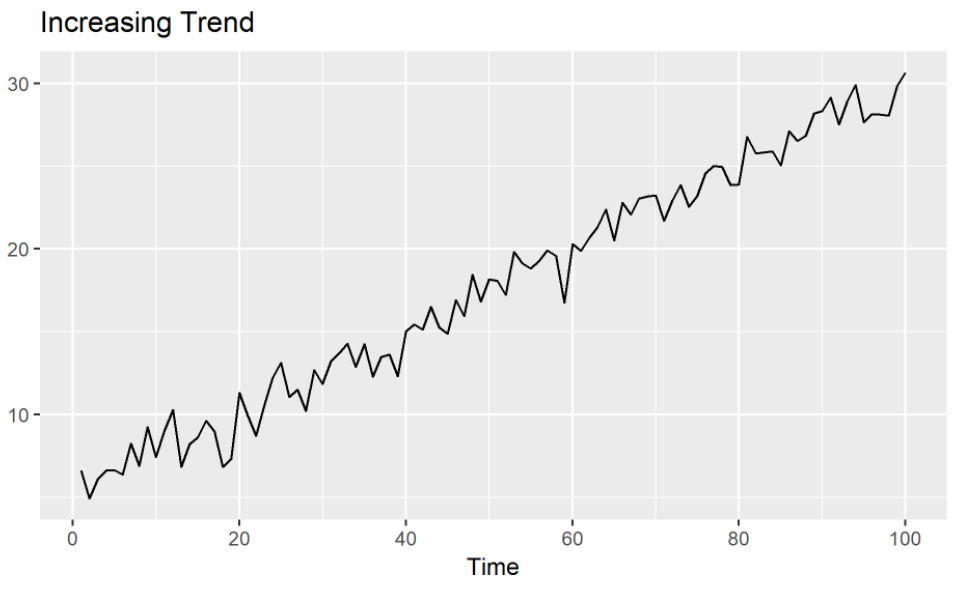
(2) 추세 ( Trend, \(T_t\) )
- 정의 :시계열이 시간에 따라 증가, 감소 또는 일정 수준을 유지하는 경우
- 확률과정의 결정론적 기댓값 함수를 알아내는 것
- 확률과정(\(Y_t\))은 (1) + (2) \(\rightarrow\) \(Y_t = f(t) + Y^s_t\)
- (1) 추정이 가능한 결정론적 추세함수(\(f(t)\))
- (2) 정상확률과정(\(Y^s_t\))
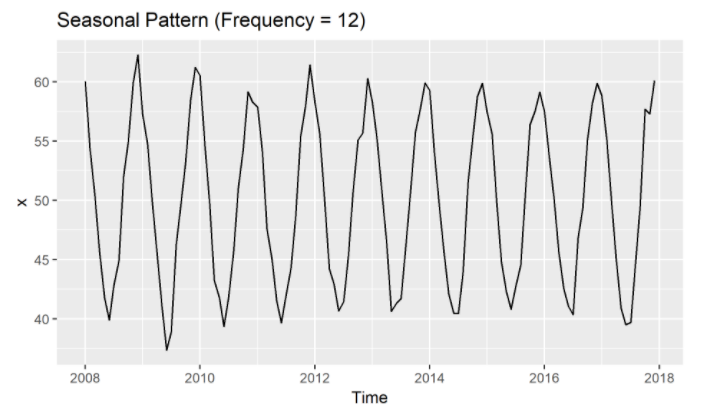
(3) 계절성 ( Seasonality, \(S_t\) )
- 정의 : 일정한 주기로 반복되어서 나타나는 패턴 (\(m\))
- ex) 특정 요일 / 특정 월 마다 반복
- ex) 12개월마다 반복되어 나타나는 경우 ( \(m=12\) )
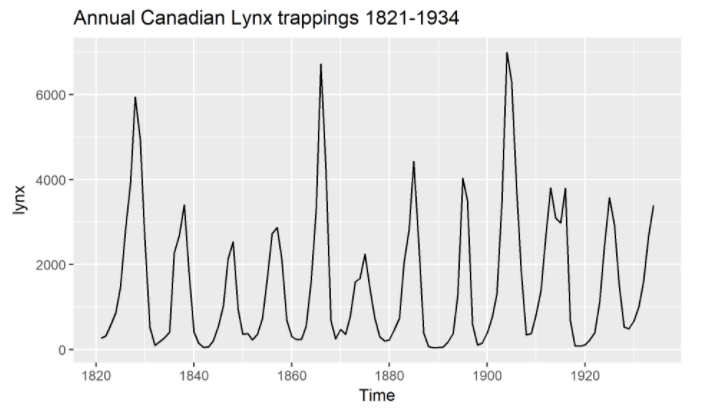
(4) 주기 ( Cycle, \(C_t\) )
-
정의 : “일정하지 않은” 빈도로 발생하는 패턴
-
주기(Cycle, \(C_t\)): 일정하지 않은 빈도로 발생하는 패턴(계절성)
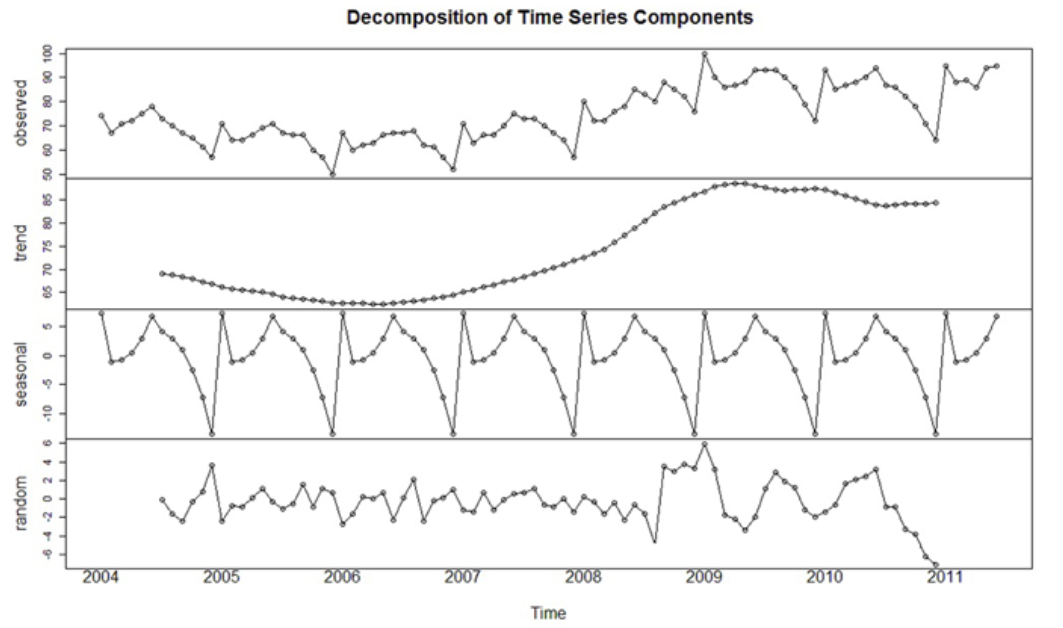
(5) 시계열 분해 ( 추세/계절성/잔차(\(e_t\)) )
(6) Dummy Variables
- 0/1 binary 형태로 변수 생성
- ex) 휴일, 이벤트, 캠페인, Outlier 등을 생성 가능
(7) 지연값 (Lagged Values, \(Lag_t(X_1)\) )
- 변수의 지연된 값을 독립변수로 사용
- 이를 사용하는 대표적 모델들 : ARIMA/VAR/NNAR
(8) 시간 변수
- 시간변수를 미시/거시 적으로 분리하거나 통합하여 생성
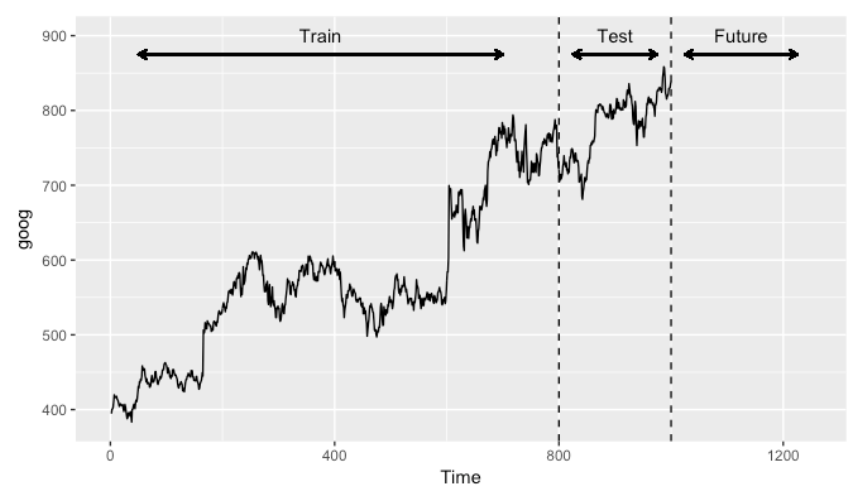
4. Time Series Validation
-
훈련셋(Training set): 가장 오래된 데이터
- 검증셋(Validation set): 그 다음 최근 데이터
- 테스트셋(Testing set): 가장 최신의 데이터
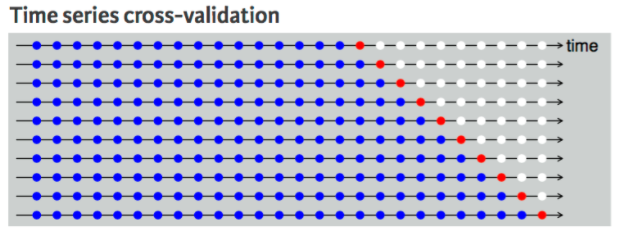
- 1스텝 교차검사(One-step Ahead Cross-validation)
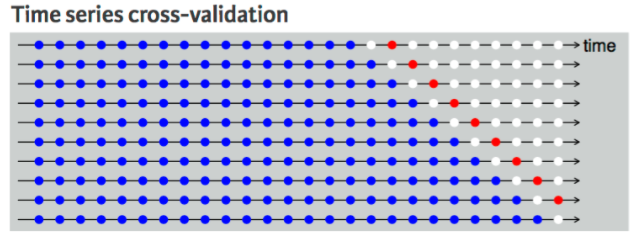
- 2스텝 교차검사(Two-step Ahead Cross-validation)
5. Time Series Model
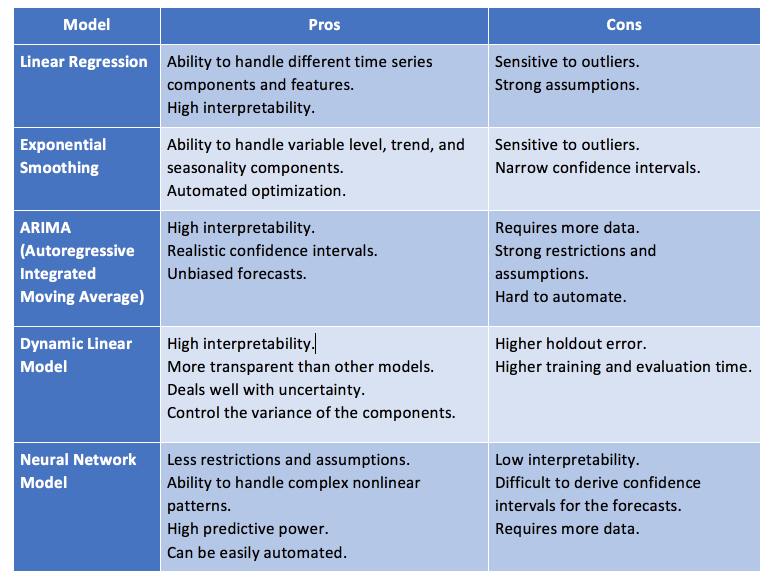
Dynamic Linear Model:
-
Bayesian-based Models
-
Generalized Autoregressive Conditional Heteroskedasticity(GARCH)
Nueral Network Model:
-
Neural Networks Autoregression(NNAR)
-
Recurrent Neural Network(RNN)
-
Long Short-Term Memory(LSTM)
-
Gated Recurrent Unit(GRU)
6. Residual Diagnostics ( 잔차 진단 )
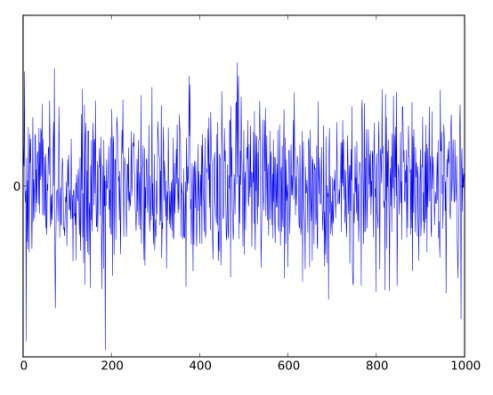
(1) 백색 잡음 (White Noise)
백색 잡음이라 하기 위해선, 2가지 조건이 필요함
- 조건 1) 잔차들은 정규분포 & ( 평균=0, 일정한 분산 )
- \(\epsilon_t \sim N(0,\sigma^2_{\epsilon_t})\), where \(\epsilon_t = Y_t - \hat{Y_t}\)
- \(Cov(\epsilon_s, \epsilon_k) = 0\) for different times! \((s \ne k)\)
- 조건 2) 잔차들이 시간의 흐름에 따라 상관성이 없어야 함
- 아래 참조
(2) 자기상관함수 (Autocorrelation Function, ACF)
-
AUTOcorrelation=0인지 확인하기 위해
( 자기 자신에 대해, 다른 시간에 대해서 correlation 없어! )
-
용어 정리
- 1) 공분산(Covariance)
- \(Cov(\epsilon_s, \epsilon_k)\) = \(E[(\epsilon_s-E(\epsilon_s))\)\((\epsilon_k-E(\epsilon_k))]\) = \(\gamma_{s,k}\)
- 2) 자기상관함수(Autocorrelation Function)
- \(Corr(\epsilon_s, \epsilon_k)\) = \(\dfrac{Cov(\epsilon_s, \epsilon_k)}{\sqrt{Var(\epsilon_s)Var(\epsilon_k)}}\) = \(\dfrac{\gamma_{s,k}}{\sqrt{\gamma_s \gamma_k}}\)
- 3) 편자기상관함수(Partial Autocorrelation Function) : \(s\)와 \(k\)사이의 상관성을 제거한 자기상관함수
- \(Corr[(\epsilon_s-\hat{\epsilon}_s, \epsilon_{s-t}-\hat{\epsilon}_{s-t})]\) for \(1<t<k\)
- 1) 공분산(Covariance)
자기상관테스트
- 1) 시각화로 검증
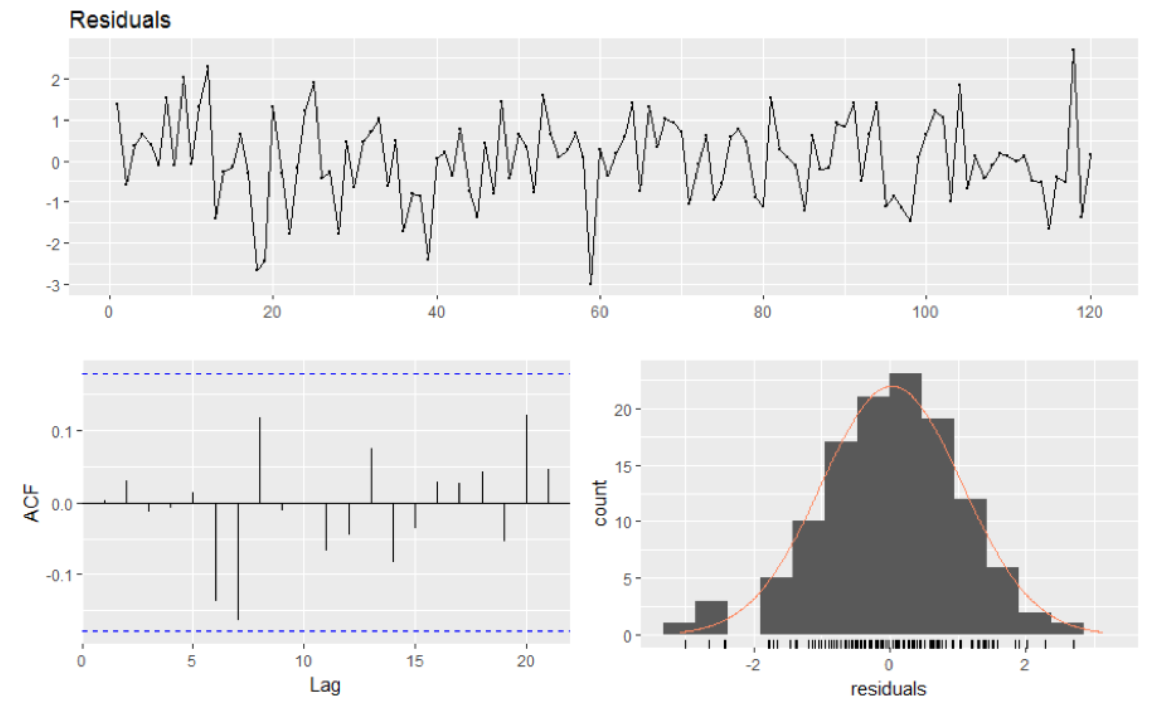
- 2) 통계량으로 검증
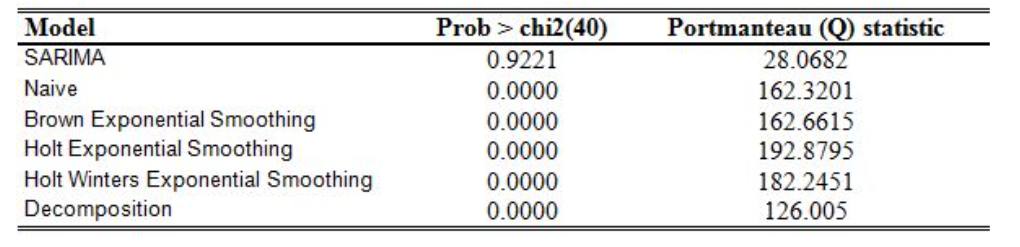
7. 4가지 잔차진단 test
- 정상성 test
- 정규분포 test
- 자기상관 test
- 등분산성 test
(1) 정상성 test
정상성 = “자기상관 X & 등분산성”을 하나로 아우르는 개념
-
시간이 지나도 특별한 형태 X ( stationary )
-
examples)
- **Augmented Dickey-Fuller(ADF) test **… p-value가 작으면 “정상”
- ADF-GLS test … p-value가 작으면 “정상”
- Phillips–Perron(PP) test … p-value가 작으면 “정상”
- Kwiatkowski Phillips Schmidt Shin(KPSS) test … p-value가 작으면 “비정상”
(2) 정규분포 test
- **Shapiro–Wilk test ** … p-value가 작으면 “정규분포 X” ( 이하 동일)
- Kolmogorov–Smirnov test
- Lilliefors test
- Anderson–Darling test
- Jarque–Bera test
- Pearson’s chi-squared test
- D’Agostino’s K-squared test
(3) 자기상관 test
-
**Ljung–Box test **… p-value가 작으면 “Autocorrelation 존재”
-
Breusch–Godfrey test .. 동일
-
검정통계량 범위 - \([0, 4]\)
-
2 근방:
\(\rightarrow\) 시계열 데이터의 Autocorrelation은 존재하지 않는다
-
0 또는 4 근방:
- 0 근방 : 양의 autocorrelation
- 4 근방 : 음의 autocorrelation
-
(4) 등분산성 test
- **Goldfeld–Quandt test **… p-value가 작으면 “등분산성 X” (이하 동일)
- Breusch–Pagan test
- Bartlett’s test
