Seunghan Lee

Seunghan Lee

Deep Learning, Data Science, Statistics

참고 : https://otexts.com/fppkr/

[ 시계열 분해 ]

1. 시계열 성분

(1) Introduction

시계열 덧셈 분해 : $y_{t}=S_{t}+T_{t}+R_{t}$

시계열 곱셈 분해 : $y_{t}=S_{t} \times T_{t} \times R_{t}$

  • 3가지 성분

    • $T_t$ : 추세-주기 성분
    • $S_t$ : 계절 성분
    • $R_t$ : 잔차

  • 위 세 값 모두 양(+)의 값

  • 계절성 요동의 크기 / 추세 주기 주위의 변동이, $t$에 따라 변하지 않는 이상 “덧셈 분해”

    ( 주로 경제 분야 : 곱셈 분해 )

  • 사실상, “곱셈 분해” = “(로그) 덧셈 분해”

    • $\log y_{t}=\log S_{t}+\log T_{t}+\log R_{t}$.


(2) Seasonality 조정

“seasonally adjusted” data : $y_t - S_t$ ( 혹은 $y_t/S_t$ )

  • case : 계절성에 의한 변동이 주된 관심사가 아닐 때

    ( 비계절성 변동에 관심이 있을 때 )

    • ex) 연초/연말에는 사람들이 많이 감기걸리는건 당연한 사실
    • ex) “실업률” 데이터


2. Moving Average

(1) MA

$m-$MA : $\hat{T}{t}=\frac{1}{m} \sum{j=-k}^{k} y_{t+j}$

  • $m$ : 차수 (order)
  • $m$ = $2k+1$
    • 좌/우에 $k$만큼, 가운데에 $1$


(2) MA의 MA

MA의 MA = 중심화된 이동평균(centered moving average)

  • 짝수 차수 이동 평균을 대칭적으로 만들기 위해서
  • 주요 용도 : $T_t$ 파악 위해!
  • ex) “$2×4-$MA” : 4-MA 를 구하고 나서 2-MA를 구함
    • $\begin{aligned} \hat{T}{t} &=\frac{1}{2}\left[\frac{1}{4}\left(y{t-2}+y_{t-1}+y_{t}+y_{t+1}\right)+\frac{1}{4}\left(y_{t-1}+y_{t}+y_{t+1}+y_{t+2}\right)\right]
      &=\frac{1}{8} y_{t-2}+\frac{1}{4} y_{t-1}+\frac{1}{4} y_{t}+\frac{1}{4} y_{t+1}+\frac{1}{8} y_{t+2} . \end{aligned}$.


일반화 :

  • $2m-$MA = (m+1) 차수의 “weighted” MA
    • 첫 번째 / 마지막 : $1/(2m)$의 가중치
    • 나머지 : $1/m$의 가중치
  • 계절성 주기가…
    • 짝수이면서 차수 m일 경우 : $2\times m-$MA를 사용
    • 홀수이면서 차수 m일 경우 : $m-$MA를 사용
  • ex)
    • $2 \times 12$-MA : “월별” data의 $T_t$ 파악 위해
    • $7$-MA : “1주일 주기성” data의 $T_t$ 파악 위해


(3) Weighted MA

가중합 : $\hat{T}{t}=\sum{j=-k}^{k} a_{j} y_{t+j}$.

  • $k = (m-1)/2$.
  • weight : $\left[a_{-k}, \ldots, a_{k}\right]$

장점 : “보다 메끄러운” Trend


3. 고전적인 분해법

(1) 소개

  • 1920년대에 창안
  • 대표적으로
    • 덧셈 분해
    • 곱셈 분해
  • 주요 가정 : “계절적인 성분이 매년 일정”
    • 이 때, $m$을 “계절성 지수”라고 부름


덧셈 (곱셈) 분해

(step 1) $m$이..

  • 짝수일 경우 : $2m$-MA

    홀수일 경우 : $m$-MA

를 사용하여 $\hat{T}_t$ 계산


(step 2) Detrend : $y_t - \hat{T}_t$ ( 곱셈 : $y_t/\hat{T_t}$ )


(step 3) 해당 계절에 대해 추세를 제거한 값의 평균 구하기 ( = $\hat{S_t}$ )

  • ex) 2000년 3월, 2001년 3월 … 2022년 3월 평균내기


(step 4) De-seasonalize : $\hat{R}{t}=y{t}-\hat{T}{t}-\hat{S}{t}$. ( 곱셈 : $\hat{R}{t}=y{t} /\left(\hat{T}{t} \hat{S}{t}\right)$ )


첨언

  • 널리 이용되지만, 추천 X ( 보다 나은방법 많음 )
  • 고전적 분해법의 특징
    • 1) 데이터의 급격한 증가/감소를 매끄럽게 함
  • 고전적 분해법의 문제점
    • 1) 첫 $k$ & 마지막 $k$ 값에 대한 추세 값을 얻을수 없음
      • ex) NA/NA/NA/5/6/6/7/7/6/5/NA/NA/NA
    • 2) 계절 성분이 매년 반복된다는 강한 가정
    • 3) 특이값을 다루기에 부적절
      • ex) 특정 사건 발생할 경우, 포착 X


4. X11 분해


( by 미국 인구 조사국(the US Census Bureau)과 캐나다 통계청(Statistics Canada))

  • 분기별 데이터 & 월별 데이터 분해할 때
  • 고전적 분해의 단점 극복 위해
    • 장점 1) (양 끝 $2k$점을 포함한) 모든 관측값에 대해 Trend 추정 가능
    • 장점 2) 계절 성분이 시간에 따라 느리게 변함
    • 장점 3) 거래일 변동 / 휴일 효과 / 알려진 예측치 등의 효과도 ( 자동 ) 고려 O


X11 details

  • 1) iterative process
  • 2) appropriate moving averages
  • 3) trend, cycle, seasonal, and irregular components
    • $T_t$ , $C_t$, $S_t$ , $I_t$


Procedure

  • step 1) Trend/Cycle 추정
    • MA filter 사용
  • step 2) De-Trend/Cycle
    • 남은건 Seasonal or Irregular
  • step 3) Seasonality 추정
  • step 3) De-Seasonality


Initial Estimates : $A_t$

  • first estimate of the seasonally adjusted series : $A_{t}=\widehat{T}{t}+\widehat{I}{t}$


Estimate Extreme Values

  • from $\hat{I_t}$ , can identify extremes and outliers


Iteration

  • 시작점 : ( seasonality가 줄어든 ) $A_t$
  • iterate
    • 1) trend 추정 ( Trend MA filter 사용 )
    • detrend
    • 2) seasonality 추정 ( Seasonal MA filter 사용 )
    • 3) extreme Values 찾기


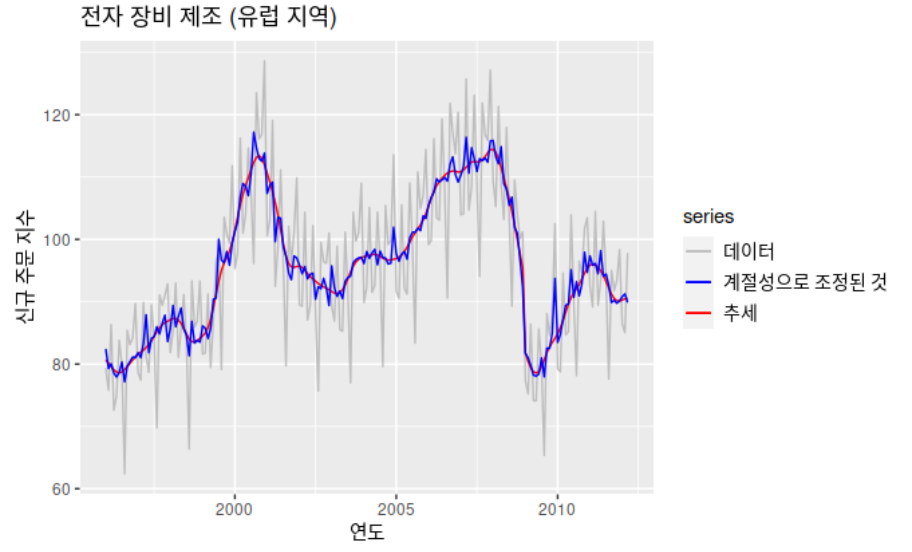
figure2


5. SEATS 분해

Dagum, E. B., & Bianconcini, S. (2016). Seasonal adjustment methods and real time trend-cycle estimation. Springer


Seasonal Extraction in ARIMA Time Series

(ARIMA 시계열에서 계절성 추출)


단점 : 분기별 데이터와 월별 데이터에서만 작동


6. STL 분해

https://www.wessa.net/download/stl.pdf

  • 다양한 상황에서 사용 가능
  • STL = Seasonal & Trend decomposition using Loess
  • Loess : 비선형 관계를 추정하기 위한 기법


LOESS / LOWESS

  • 참고 : https://www.youtube.com/watch?v=Vf7oJ6z2LCc

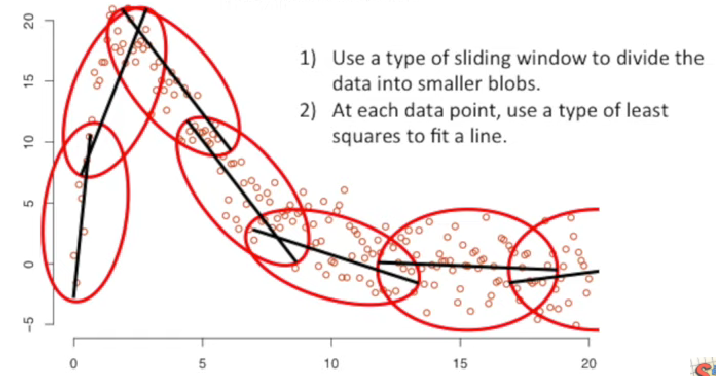
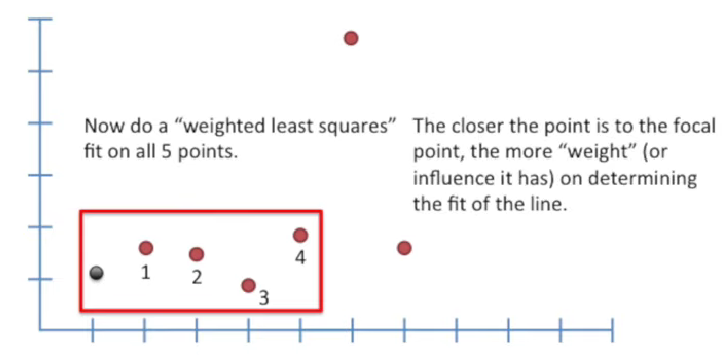
figure2

figure2

figure2


  • 1번째 focal point 예측완료

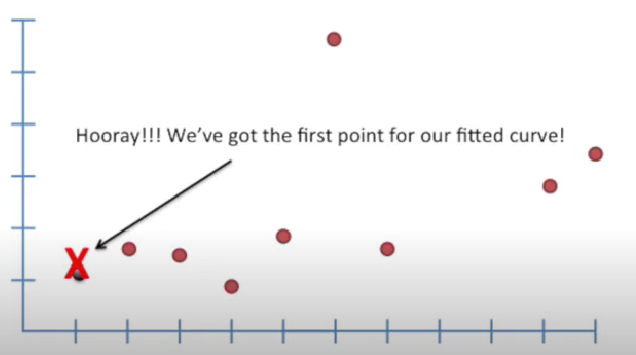
figure2


  • 2번째 focal point에 대해서 마찬가지로 진행

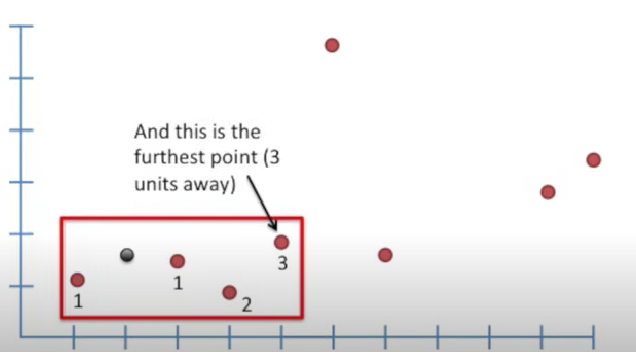
figure2


  • 3번째 ~

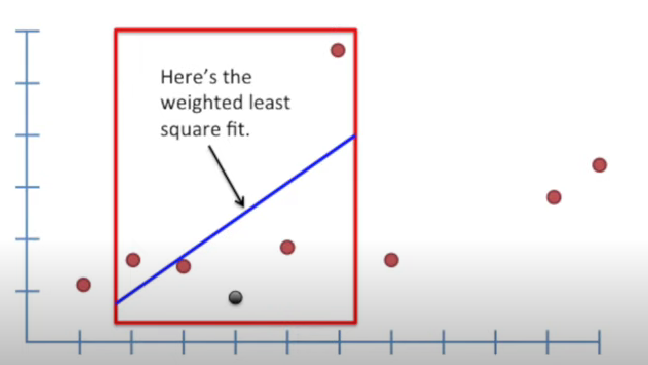
figure2


  • 4번째 ~

figure2


  • 결론 : smooth curve

figure2


위에서 fitting 시키는 과정에서, 다양한 함수 사용 가능

  • ex) weighted least squares / parabolas …

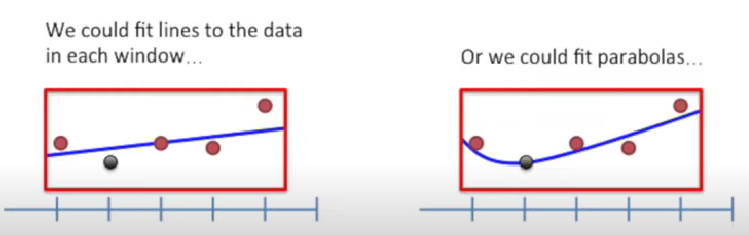
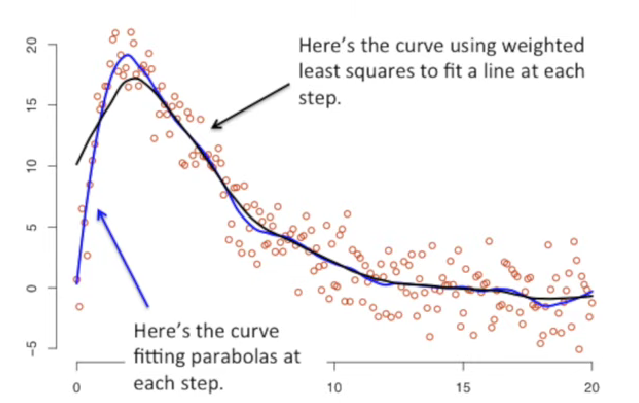
figure2

figure2


R에서..

  • lowess() : fit a line
  • loess() : fit a line or a parabola


STL > SEATS, X11

  • 어떤 종류의 계절성도 OK
  • 계절적인 성분이 시간에 따라 변해도 OK
  • Trend/Cycle의 매끄러운 정도를 사용자가 조절
  • 일부 이상치들이이 Trend/Cycle와 Seasonality에 영향 끼치지 X 도록 OK


7. Trend & Seasonality 강도 측정

$F_{T}=\max \left(0,1-\frac{\operatorname{Var}\left(R_{t}\right)}{\operatorname{Var}\left(T_{t}+R_{t}\right)}\right)$.

$F_{S}=\max \left(0,1-\frac{\operatorname{Var}\left(R_{t}\right)}{\operatorname{Var}\left(S_{t}+R_{t}\right)}\right)$.


You May Also Enjoy

3 minute read

6 minute read

4 minute read

less than 1 minute read