참고 : https://otexts.com/fppkr/
[ ARIMA 모델 ]
1. 정상성과 차분
(1) 정상성
정상성 = 시계열이 관측된 시간에 무관
( 장기적으로 볼 때 예측할 수 있는 패턴을 나타내지 않을 것 )
- 추세 or 계절성 존재 \(\rightarrow\) 정상성 X
- 백색잡음 \(\rightarrow\) 정상성 O
주의 : (추세 X, 계절성 X, 주기성 O) 시계열은 정상성 O
- 주기가 고정된 길이를 갖고 있지 않기 때문에, 시계열을 관측하기 전에 주기의 고점이나 저점이 어디일지 확실하게 알 수 없기 때문에
(2) 차분 (differencing)
차분 = 연이은 관측값들의 차이를 계산
분산이 다를 경우 : “로그 변환”
정상성 여부 test : with “ACF plot”
- 정상성 X : ACF 느리게 감소
- 정상성 O : ACF 빠르게 감소
(3) 확률 보행 모델
차분한 새로운 시계열 : \(y'\)
-
\(y_{t}^{\prime}=y_{t}-y_{t-1}\).
( 단, 첫 번째 관측값은 차분값 계산 불가 )
만약 차분한 시계열이 백색 잡음(WN)이라면….
- 기존 시계열 (1) : \(y_{t}-y_{t-1}=\varepsilon_{t}\)
- \(\varepsilon_t\) : white noise
- 기존 시계열 (2) : \(y_{t}=y_{t-1}+\varepsilon_{t}\)
- Random Walk (확률 보행) 모델
- 정상성을 나타내지 않는 데이터 ( 특히 금융/경제 데이터를 다룰 때 ) 사용
(4) 2차 차분
차분을 해도, 정상성이 안보인다면?
\(\rightarrow\) 2차 차분해보기
\(\begin{aligned} y_{t}^{\prime \prime} &=y_{t}^{\prime}-y_{t-1}^{\prime} \\ &=\left(y_{t}-y_{t-1}\right)-\left(y_{t-1}-y_{t-2}\right) \\ &=y_{t}-2 y_{t-1}+y_{t-2} . \end{aligned}\).
(5) 계절성 차분
계절성 차분 = 관측치와, 같은 계절의 이전 관측값과의 차이
- \(y_{t}^{\prime}=y_{t}-y_{t-m}\).
- \(m\) : 계절의 개수
- 다른 표현 : \(y_{t}=y_{t-m}+\varepsilon_{t}\)
계절성 차분 + 일반 차분
\(\begin{aligned} y_{t}^{\prime \prime} &=y_{t}^{\prime}-y_{t-1}^{\prime} \\ &=\left(y_{t}-y_{t-m}\right)-\left(y_{t-1}-y_{t-m-1}\right) \\ &=y_{t}-y_{t-1}-y_{t-m}+y_{t-m-1} \end{aligned}\).
- if 데이터에 계절성 패턴이 강하면 … 계절성 차분을 먼저 계산!
(6) 단위근 검정 (Unit Root Test)
- 차분을 구하는 것이 필요할지 결정하기 위해!
- ex) PSS 검정
- \(H_0\) : 정상성 O
- \(H_A\) : 정상성 X
2. 후방 이동 기호
시계열 시차를 다룰 떄 유용한 표기법
- \(B\) : “데이터를 한 시점 뒤로” 옮기는 효과
- 적용
- 1번 적용 시 : \(B y_{t}=y_{t-1}\)
- 2번 적용 시 : \(B\left(B y_{t}\right)=B^{2} y_{t}=y_{t-2} .\)
“차분을 구하는 과정”에서 사용하기 편리
- 1차 차분 :
- \(y_{t}^{\prime}=y_{t}-y_{t-1}=y_{t}-B y_{t}=(1-B) y_{t}\).
- 2차 차분 :
- \(y_{t}^{\prime \prime}=y_{t}-2 y_{t-1}+y_{t-2}=\left(1-2 B+B^{2}\right) y_{t}=(1-B)^{2} y_{t}\).
- d차 차분 :
- \((1-B)^{d} y_{t}\).
“연산자” 사용하여 차분 시, 보통의 대수 법칙을 사용가능!
\(\rightarrow\) \(B\)를 포함하는 항은 서로 곱셈 가능
- ex) 1차 차분 & 계절성 차분
- \(\begin{aligned} (1-B)\left(1-B^{m}\right) y_{t} &=\left(1-B-B^{m}+B^{m+1}\right) y_{t} \\ &=y_{t}-y_{t-1}-y_{t-m}+y_{t-m-1} \end{aligned}\).
3. 자기회귀 모델 (Autoregressive Model)
AR(p) : 차수 \(p\)의 AR
- (1 시점 이전 ~ p 시점 이전) 모두 고려
- \(y_{t}=c+\phi_{1} y_{t-1}+\phi_{2} y_{t-2}+\cdots+\phi_{p} y_{t-p}+\varepsilon_{t}\).
AR(1)의 특징
- \(\phi_{1}=0\) : \(y_{t}\) 는 WN
- \(\phi_{1}=1\) & \(c=0\) 일 때, \(y_{t}\) 는 Random Walk
- \(\phi_{1}=1\) & \(c \neq 0\) 일 때, \(y_{t}\) 는 표류가 있는 Random Walk
- \(\phi_{1}<0\) : \(y_{t}\) 는 평균값을 중심으로 진동
AR모델을 적용하기 위해선, 우선 “정상성을 확보” 한 뒤에!
제한 조건 :
- \(\mathrm{AR}(1)\) : \(-1<\phi_{1}<1\)
- \(\mathrm{AR}(2)\) : \(-1<\phi_{2}<1, \phi_{1}+\phi_{2}<1, \phi_{2}-\phi_{1}<1\)
4. 이동 평균 모델 (Moving Average)
MA(q) : 차수 \(q\)의 MA
- \(y_{t}=c+\varepsilon_{t}+\theta_{1} \varepsilon_{t-1}+\theta_{2} \varepsilon_{t-2}+\cdots+\theta_{q} \varepsilon_{t-q}\).
- \(\varepsilon\) : WN
- 과거 몇 개의 예측 오차(forecast error)의 가중 이동 평균
- 주로 “과거 값의 추세-주기”를 측정할 때 사용
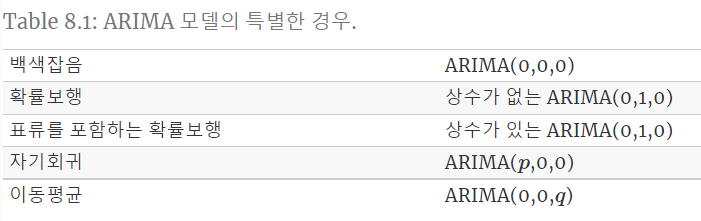
5. 비계절성 ARIMA
Autoregressive Integrated Moving Average
- \(y_{t}^{\prime}=c+[\phi_{1} y_{t-1}^{\prime}+\cdots+\phi_{p} y_{t-p}^{\prime}]+[\theta_{1} \varepsilon_{t-1}+\cdots+\theta_{q} \varepsilon_{t-q}]+\varepsilon_{t}\).
- \(y_t'\) : (1번 이상) 차분한 시계열
- ARJMA (p,d,q)
- \(p\) : AR 부분의 차수
- \(q\) : MA 부분의 차수
- \(d\) : 1차 차분의 횟수
후방이동 (Backshift) 기호 사용해서
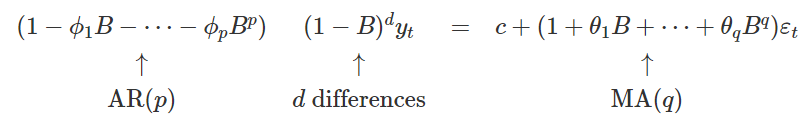
6. Auto ARIMA
힌드만-칸다카르(Hyndman-Khandakar) 알고리즘
- 단위 근 검정
- AICc 최소화
- MLE를 결합

7. 계절성 ARIMA
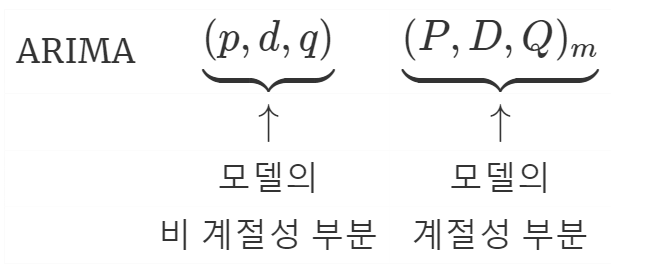
- \(m\) : 매년 관측값의 개수
Ex) 분기(4)별 데이터 : ARIMA(1,1,1)(1,1,1\()_4\)
- \(\left(1-\phi_{1} B\right)\left(1-\Phi_{1} B^{4}\right)(1-B)\left(1-B^{4}\right) y_{t}=\left(1+\theta_{1} B\right)\left(1+\Theta_{1} B^{4}\right) \varepsilon_{t}\).
8. ARIMA vs ETS
-
모든 ETS 모델은 정상성을 나타내지 않는 경우에 맞지만,
-
몇몇 ARIMA 모델은 정상성을 나타내는 경우에 맞음
