AAA (All About AI)

Gradient Boosting Neural Networks: GrowNet

https://arxiv.org/abs/2002.07971

Contents

1. Abstract
2. Introduction
3. Model
   1. GrowNet
   2. Corrective Step
4. Application
   1. Regression: MSE loss
   2. Classification: BCE loss

Abstract

Grownet

• gradient boosting ( multiple shallow models ) + NN
• outperform SOTA boosting methods in 3 tasks on multiple datasets

1. Introduuction

DT vs DNN

• DT) not unversally applicable ( ex. NLP, CV )
• DNN) perform much better

GrowNet

• builds NN from the ground up layer by layer

  ( + with idea of gradient boosting )

2. Model

Key Idea of gradient boosting : simple, lower-order models

• use shallow NN

As each boosting step, augment original input features with the output from the penultimate layer of the current iteration.

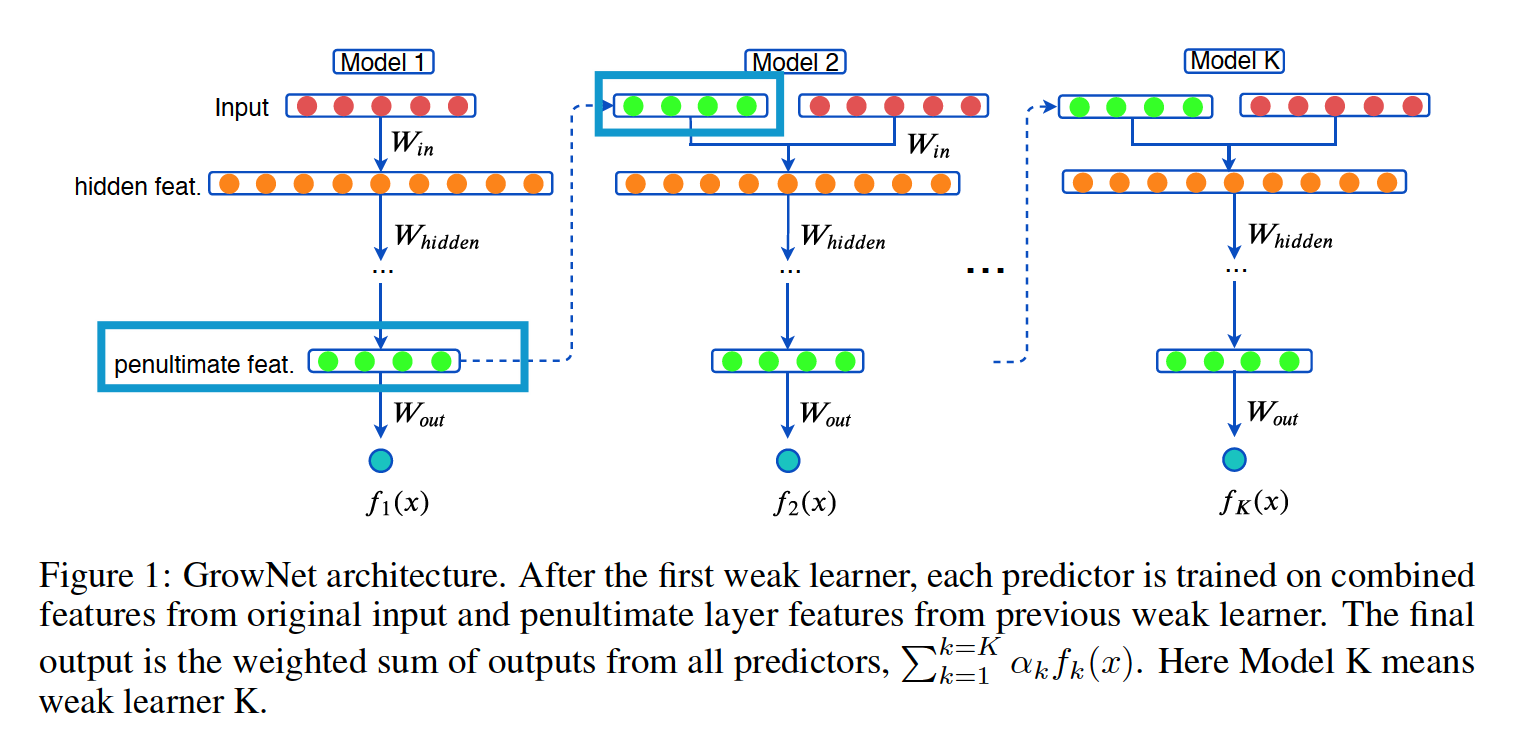
(1) Gradient Boosting NN: GrowNet

Dataset : \(\mathcal{D}=\left\{\left(\boldsymbol{x}_i, y_i\right)_{i=1}^n \mid \boldsymbol{x}_i \in\right.\) \(\left.\mathbb{R}^d, y_i \in \mathbb{R}\right\}\).

Prediction :\(K\) additive functions

• \[\hat{y}_i=\mathcal{E}(\boldsymbol{x}_i)=\sum_{k=0}^K \alpha_k f_k(\boldsymbol{x}_i)\]
  • weighted sum of \(f_k\) ‘s in GrowNet.
  • \(f_k \in \mathcal{F}\), where \(\mathcal{F}\) is the space of MLP
  • \(\alpha_k\) : the step size (boost rate).
• Each function \(f_k\) represents an independent, shallow NN

Loss Function: \(\mathcal{L}(\mathcal{E})=\sum_{i=0}^n l\left(y_i, \hat{y}_i\right)\).

Greedy search

• \(\hat{y}_i^{(t-1)}=\sum_{k=0}^{t-1} \alpha_k f_k\left(\boldsymbol{x}_i\right)\) : output of GrowNet at stage \(t-1\) for the sample \(\boldsymbol{x}_i\).

• greedily seek the next weak learner \(f_t(\mathbf{x})\) that will minimize the loss at stage \(t\)

  • \(\mathcal{L}^{(t)}=\sum_{i=0}^n l\left(y_i, \hat{y}_i^{(t-1)}+\alpha_t f_t\left(\mathbf{x}_i\right)\right)\).

Taylor expansion of the loss function \(l\)

• to ease the computational complexity.

• objective function for the weak learner \(f_t\) can be simplified as..

  \(\mathcal{L}^{(t)}=\sum_{i=0}^n h_i\left(\tilde{y}_i-\alpha_t f_t\left(\boldsymbol{x}_i\right)\right)^2\).

  • where \(\tilde{y}_i=-g_i / h_i\)
    • \(g_i\) : second order gradients of \(l\) at \(\boldsymbol{x}_i\), w.r.t. \(\hat{y}_i^{(t-1)}\)
    • \(h_i\) : second order gradients of \(l\) at \(\boldsymbol{x}_i\), w.r.t. \(\hat{y}_i^{(t-1)}\)

(2) Corrective Step (C/S)

Traditional boosting : each weak learner is greedily learned

\(\rightarrow\) local minimia ( + due to fixed boosting rate \(\alpha_k\) )

Solution: corrective step

\(\rightarrow\) instead of fixing the previous \(t-1\) weak learners…

update the parameters of ALL previous \(t-1\) weak learners!

3. Application

Regression & Classifcation & Learning to Rank

(1) Regression: MSE loss

• \(g_i=2\left(\hat{y}_i^{(t-1)}-y_i\right)\);
• \(h_i=2\).
• \(\tilde{y}_i=y_i-\hat{y}_i^{(t-1)}\).

Train next weak learner \(f_t\) by least square regression on \(\left\{\boldsymbol{x}_i, \tilde{y}_i\right\}\) for \(i=1,2, \ldots, n\).

(2) Classification: BCE loss

• \(g_i=\frac{-2 y_i}{1+e^{2 y_i \hat{y}_i^{(t-1)}}}\).
• \(h_i=\frac{4 y_i^2 e^{2 y_i \hat{y}_i^{(t-1)}}}{\left(1+e^{2 y_i \hat{y}_i^{(t-1)}}\right)^2}\).
• \(\tilde{y}_i=-g_i / h_i=y_i\left(1+e^{-2 y_i \hat{y}_i^{(t-1)}}\right) / 2\).