Wav2Vec 2; A Framework for Self-Supervised Learning of Speech Representations

wav2vec 2.0; A Framework for Self-Supervised Learning of Speech Representations ( NeurIPS 2020 )

https://arxiv.org/pdf/2006.11477.pdf

Contents

1. Abstract
2. Model
   1. Feature encoder
   2. Contextualized representations with Transformers
   3. Quantization module
3. Training
   1. Masking
   2. Objective

Abstract

Learning powerful representations from speech audio alone followed by fine-tuning on transcribed speech can outperform the best semi-supervised methods!

wav2vec 2.0

• masks the speech input in the latent space
• solves a contrastive task defined over a quantization of the latent representations which are jointly learned.

1. Model

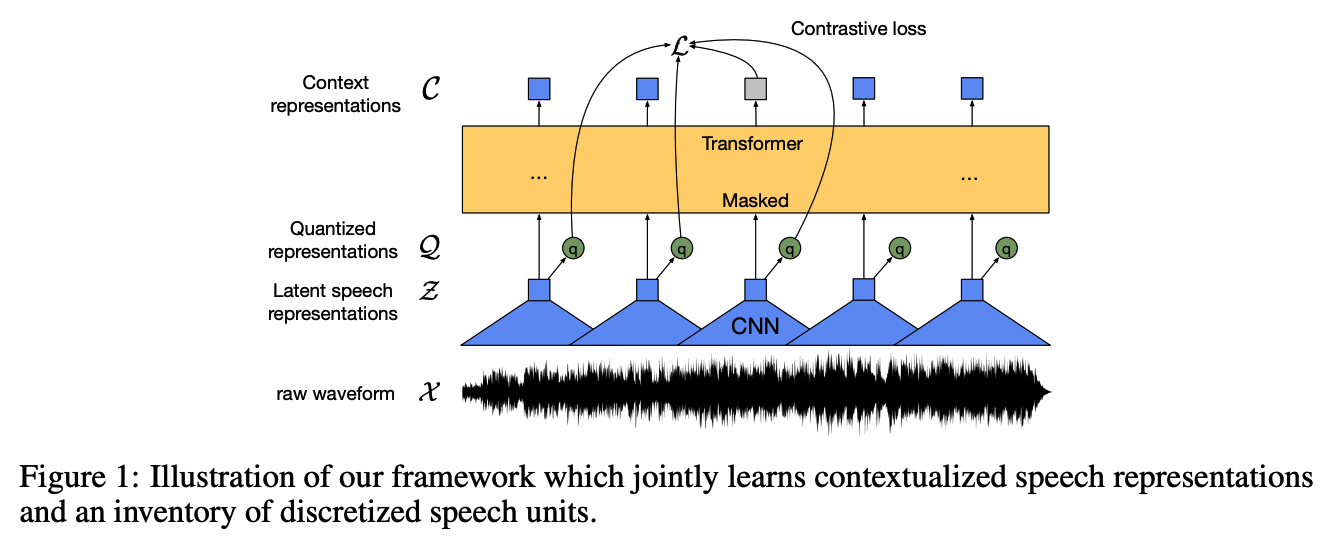
(1) Multi-layer CNN feature encoder \(f: \mathcal{X} \mapsto \mathcal{Z}\)

• input = raw audio \(\mathcal{X}\)
• output = latent speech representations \(\mathbf{z}_1, \ldots, \mathbf{z}_T\) for \(T\) time-steps.
  • output is discretized to \(\mathbf{q}_t\)
    • via a quantization module \(\mathcal{Z} \mapsto \mathcal{Q}\)
    • to represent the targets in the self-supervised objective

(2) Transformer \(g: \mathcal{Z} \mapsto \mathcal{C}\)

• to build representations \(\mathbf{c}_1, \ldots, \mathbf{c}_T\) capturing information from the entire sequence

Comparison with VQ-wav2vec

• wav2vec 2.0 = builds context representations over continuous speech representations and self-attention captures dependencies over the entire sequence of latent representations end-to-end.

(1) Feature encoder

Architecture

• consists of several blocks containing a temporal convolution
• followed by LayerNorm & GeLU
• total stride of the encoder determines the number of time-steps \(T\)
  • which are input to the Transformer

Input : raw waveform

• normalized to zero mean and unit variance

(2) Contextualized representations with Transformers

use Transformer as a context network

Input = output of the feature encoder

Positional embedding

• fixed positional embeddings (X)
  • encode absolute positional information
• use a convolutional layer which acts as relative positional embedding (O)

(3) Quantization module

Discretize the output of the feature encoder \(\mathbf{z}\) to a finite set of speech representations via product quantization

Product quantization

• learn discrete units & then learning contextualized representations
• choosing quantized representations from multiple codebooks and concatenating them
  • mulitple codebooks = \(G\) codebooks with \(V\) entries \(e \in\) \(\mathbb{R}^{V \times d / G}\)
• How?
  • step 1) choose one entry from each codebook
  • step 2) oncatenate the resulting vectors \(e_1, \ldots, e_G\)
  • step 3) linear transformation \(\mathbb{R}^d \mapsto \mathbb{R}^f\) to obtain \(\mathbf{q} \in \mathbb{R}^f\).
• use Gubmel softmax to make it differentiable

Result :

• \(\mathbf{z}\) is mapped to \(\mathbf{l} \in \mathbb{R}^{G \times V}\) logits

• Probabilities for choosing the \(v\)-th codebook entry for group \(g\) are

  • \(p_{g, v}=\frac{\exp \left(l_{g, v}+n_v\right) / \tau}{\sum_{k=1}^V \exp \left(l_{g, k}+n_k\right) / \tau}\).
  • \(n=-\log (-\log (u))\) and \(u\) are uniform samples from \(\mathcal{U}(0,1)\).

Forward & Backward pass

• Forward pass : codeword \(i\) is chosen by \(i=\operatorname{argmax}_j p_{g, j}\)
• Backward pass : true gradient of the Gumbel softmax outputs is used

3. Training

Identifying the correct quantized latent audio representation in a set of distractors for each masked time step

(1) Masking

• mask a proportion of the feature encoder outputs

• replace them with a trained feature vector shared between all masked time steps

  • ( of course, do not mask inputs to the quantization module )

• masking = randomly sample without replacement a certain proportion \(p\) of all time steps to be starting indices & then mask the subsequent \(M\) consecutive time steps

  ( \(\therefore\) can be overlapped )

(2) Objective

a) Contrastive task \(\mathcal{L}_m\)

• identify the true quantized latent speech representation for a masked time step within a set of distractors

b) Codebook diversity loss \(\mathcal{L}_d\)

• to encourage the model to use the codebook entries equally often.

\(\rightarrow\) Final Loss : \(\mathcal{L}=\mathcal{L}_m+\alpha \mathcal{L}_d\)

a) Contrastive Loss

\(\mathcal{L}_m=-\log \frac{\exp \left(\operatorname{sim}\left(\mathbf{c}_t, \mathbf{q}_t\right) / \kappa\right)}{\sum_{\tilde{\mathbf{q}} \sim \mathbf{Q}_t} \exp \left(\operatorname{sim}\left(\mathbf{c}_t, \tilde{\mathbf{q}}\right) / \kappa\right)}\).

Goal : needs to identify the true quantized latent speech representation \(\mathbf{q}_t\)

• among a set of \(K+1\) quantized candidate representations \(\tilde{\mathbf{q}} \in \mathbf{Q}_t\)
  • \(\mathbf{Q}_t\) includes \(\mathbf{q}_t\) and \(K\) distractors, wheredistractors are uniformly sampled from other masked time steps of the same utterance.

b) Diversity Loss

Contrastive task depends on the codebook

\(\rightarrow\) diversity loss \(\mathcal{L}_d\) is designed to increase the use of the quantized codebook

\(\rightarrow\) encourage the equal use of the \(V\) entries in each of the \(G\) codebooks

• by maximizing the entropy of the averaged softmax distribution \(\mathbf{1}\) over the codebook entries for each codebook \(\bar{p_g}\) across a batch of utterances

\(\mathcal{L}_d=\frac{1}{G V} \sum_{g=1}^G-H\left(\bar{p}_g\right)=\frac{1}{G V} \sum_{g=1}^G \sum_{v=1}^V \bar{p}_{g, v} \log \bar{p}_{g, v}\).