Seunghan Lee

Seunghan Lee

Deep Learning, Data Science, Statistics

Bayes by Backprop

( 이론 참고 : https://seunghan96.github.io/bnn/06.Weight-Uncertainty-in-Neural-Networks(2015)/ )

( 코드 참고 : https://www.ritchievink.com/blog/2019/09/16/variational-inference-from-scratch/ & https://seunghan96.github.io/stat/gan/(Deep-Bayes)07.Implementation-of-VAE/ )


1. Import Packages

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.distributions as dist
import matplotlib.pyplot as plt
from dataclasses import dataclass
import numpy as np


GPU 사용 여부

  • torch.tensor( ).to(device)를 계속 사용하는 것을 피하기 위해

    Tensor = torch.cuda.FloatTensor를 사용한다.

cuda = True if torch.cuda.is_available() else False
Tensor = torch.cuda.FloatTensor if cuda else torch.FloatTensor


2. 가상 데이터 생성

아래와 같은 임의의 데이터를 생성한다.

  • Y_real : noise가 없는 Y
  • Y_noise : Y_real에 \(\epsilon \sim N(0,\sigma)\)의 noise가 낀 값
def func(x):
    return 0.2*np.power(x, 3)-2*np.power(x, 2+1)+8*x

n=20000
sigma=1.5

X = np.linspace(-3, 3, n)
Y_real = func(X)
Y_noise = (Y_real+np.random.normal(0,sigma,n))


데이터의 모양을 보면 아래와 같다.

plt.figure(figsize=(16, 6))
plt.scatter(X, Y_noise,s=0.1)

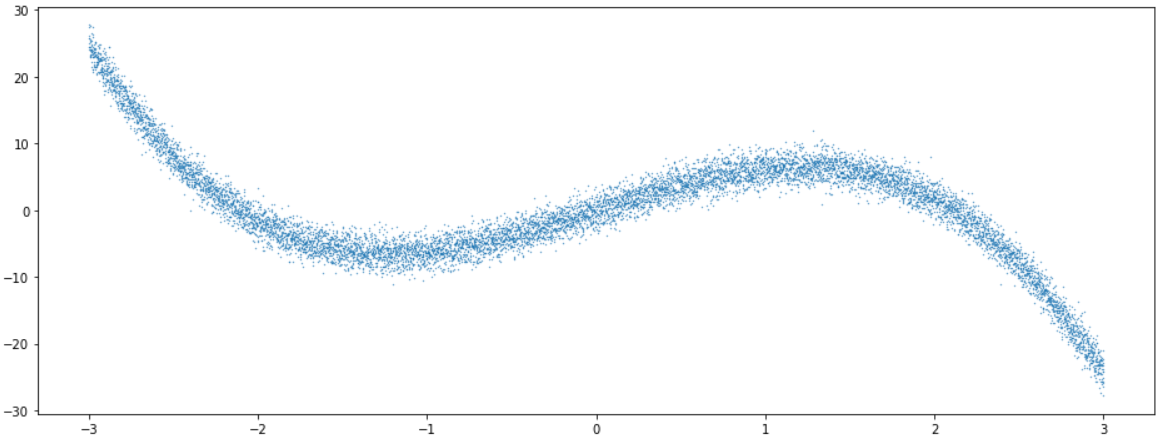
figure2


생성한 데이터를 tensor로 변환해준다.

X = Tensor(X).view(-1,1)
Y_real = Tensor(Y_real).view(-1,1)
Y_noise = Tensor(Y_noise).view(-1,1)


Train & Test split ( 8 : 2 )를 한다.

np.random.seed(1996)
val_idx = np.sort(np.random.choice(n, int(n*0.2),replace=False))
train_idx = np.array(list(set(np.arange(n))-set(val_idx)))

x_train,x_val = X[train_idx],X[val_idx]
y_train,y_val = Y_noise[train_idx],Y_noise[val_idx]


3. Modeling

  • 1) linear_vi_layer : Variational Inferece를 사용한 이 layer는, 기존의 linear layer와는 아래와 같은 차이점들이 있다.
    • (a) weight가 probabilistic하다 ( 고정된 값이 아니라, 분포를 따른다 )
    • (b) 매번 feedforward할 때마다, KL-divergence가 누적되어서 이후에 loss function 연산 시 반영된다
    • (c) reparameterization trick을 사용한다
  • 2) BBB : 여러 linear_vi_layer와 activation function을 쌓아서 만든 Bayesian Neural Network이다.


3-1. variational linear layer

  • (INPUT) input의 차원, output의 차원, parent, batch size ( mini-batch의 개수 ), bias(절편) 여부

  • Prior 설정하기

    • \[w_{\mu} \sim N(0,0.001^2)\] \[\text{log}(w_{\sigma}) \sim N(-2.5,0.001^2)\]
    • \(b_{\mu}\) 랑 \(\text{log}(b_{\sigma})\)는 deterministic하게 설정!

  • kl_div : 각 layer를 pass할때마다, kl-divergence를 누적한다

    우리의 loss function은 negative ELBO로, \(-(E_{Z \sim Q}[\underbrace{\log P(D \mid Z)}_{\text {likelihood }}]-D_{K L}(Q(Z) \mid \underbrace{P(Z)}_{\text {prior }}))\)이다.

    • first term : reconstruction loss
    • second term : KL-divergence

    우리는 여기서 두 번째 term인 KL-divergence를 구한다.

    \[D_{K L}(Q(Z) \mid P(Z))=E_{Z \sim Q}[\log P(Z)-\log Q(Z)]\] 
class linear_vi_layer(nn.Module):
  def __init__(self,input_dim,output_dim,parent,n_batch,bias=True):
    super().__init__()
    self.input_dim = input_dim
    self.output_dim = output_dim
    self.parent = parent
    self.n_batch = n_batch
    self.bias = bias
    if getattr(parent, 'cumsum_kl',None) is None:
      parent.cumsum_kl = 0
    
    self.w_mu = nn.Parameter(Tensor(input_dim,output_dim).normal_(mean=0,std=0.001))
    self.w_logstd = nn.Parameter(Tensor(input_dim,output_dim).normal_(mean=-2.5,std=0.001))
    if self.bias:
      self.b_mu = nn.Parameter(Tensor(np.zeros(output_dim)))
      self.b_logstd = nn.Parameter(Tensor(np.zeros(output_dim)))
  
  def reparam(self,mu,logstd):
    sigma = torch.log(1+torch.exp(logstd))
    eps = torch.randn_like(sigma)
    return mu + (sigma*eps)

  def kl_div(self,z,mu_theta,logstd_theta,prior_std=1):
    log_prior = dist.Normal(0,prior_std).log_prob(z) # should be LARGE
    log_p_q = dist.Normal(mu_theta,torch.log(1+torch.exp(logstd_theta))).log_prob(z) # should be SMALL
    return (log_p_q - log_prior).sum() / self.n_batch

  def forward(self,x):
    W = self.reparam(self.w_mu,self.w_logstd)
    B = 0
    if self.bias:
      B = self.reparam(self.b_mu,self.b_logstd)
    Z = torch.matmul(x,W) + B
    self.parent.cumsum_kl += self.kl_div(W,self.w_mu,self.w_logstd)
    if self.bias:
      self.parent.cumsum_kl += self.kl_div(B,self.b_mu,self.b_logstd)
    return Z


3-2. BBB ( “Bayes by Backprop” )

여러 linear_vi_layer와 activation function을 쌓아서 만든 Bayesian Neural Network이다.


@property에 대한 구체적 설명은 다음의 블로그( https://nowonbun.tistory.com/660 )를 참조하면 좋을 것 같다.

간단 요약 :

  • 외부에서 클래스 내부 변수를 참조하기 위한 함수

  • getter, setter라고도 부름

@dataclass : Class를 보다 용이하게 선언해주는 decorator

@dataclass
class KL:
  cumsum_kl=0
  
class BBB(nn.Module):
  def __init__(self,input_dim,hidden_dim,output_dim,n_layers,n_batch):
    super().__init__()
    self.kl_loss = KL
    modules = []
    for i in range(n_layers):
      if i==0:
        modules.append(linear_vi_layer(input_dim,hidden_dim,self.kl_loss, n_batch))
        modules.append(nn.ReLU())
      elif i <n_layers-1:
        modules.append(linear_vi_layer(hidden_dim,hidden_dim,self.kl_loss, n_batch))
        modules.append(nn.ReLU())
      else:
        modules.append(linear_vi_layer(hidden_dim,output_dim,self.kl_loss, n_batch))
    self.layers = nn.Sequential(*modules)

  @property
  def cumsum_kl(self):
    return self.kl_loss.cumsum_kl
  
  def reset_kl(self):
    self.kl_loss.cumsum_kl=0

  def forward(self,x):
    x = self.layers(x)
    return x


4. Loss Function

앞서 말했듯, 우리의 Loss Function은, Variational Free energy (혹은 negative ELBO)로써, 아래의 식과 같다.

\[\operatorname{argmax}_{Z}=E_{Z \sim Q}[\underbrace{\log P(D \mid Z)}_{\text {likelihood }}]-D_{K L}(Q(Z) \mid \underbrace{P(Z)}_{\text {prior }})\]

앞의 linear_vi_layer에서 누적해서 구했던 KL-divergence에, reconstruction error를 더하면 그것이 곧 우리의 최종 Loss가 된다.

def det_loss(y_real, y_pred, model):
  reconstruction_error = -dist.Normal(y_pred, .1).log_prob(y_real).sum()
  kl = model.cumsum_kl
  model.reset_kl()
  return reconstruction_error + kl


5. Train

  • model, epoch 수, optimizer, dataset을 input을 넣는다

  • 특이한 점 : loss function 계산을 위해, MSE,MAE,CrossEntropy등과는 다르게 “실제Y”와 “예측Y”뿐만 아니라, 모델 또한 넣어준다.

    왜냐하면, 우리가 정의한 loss (negative ELBO)의 일부인 KL-div term이 model에 들어있기 때문이다 (model.cumsum_kl )

def train(model,n_epoch,opt,x_train,y_train,x_val,y_val):
  for epoch in range(1,n_epoch+1):
    y_pred = model(x_train)
    y_val_pred = model(x_val)
    train_loss = det_loss(y_pred, y_train, model)
    val_loss = det_loss(y_val_pred, y_val, model)
    opt.zero_grad()
    train_loss.backward()
    opt.step()

    if epoch%500==0:
      print('Epoch %d, Train Loss %f, Val Loss %f' %(epoch,float(train_loss/x_train.shape[0]),float(val_loss/x_val.shape[0])))


6. Result & Visualization

6-1. Train

  • optimizer : Adam optimizer
n_epoch=5000
bbb = BBB(input_dim=1, hidden_dim=20,n_layers=5, output_dim=1,n_batch=1)
opt = torch.optim.Adam(bbb.parameters(), lr=0.01)
train(bbb,n_epoch,opt,x_train,y_train,x_val,y_val)

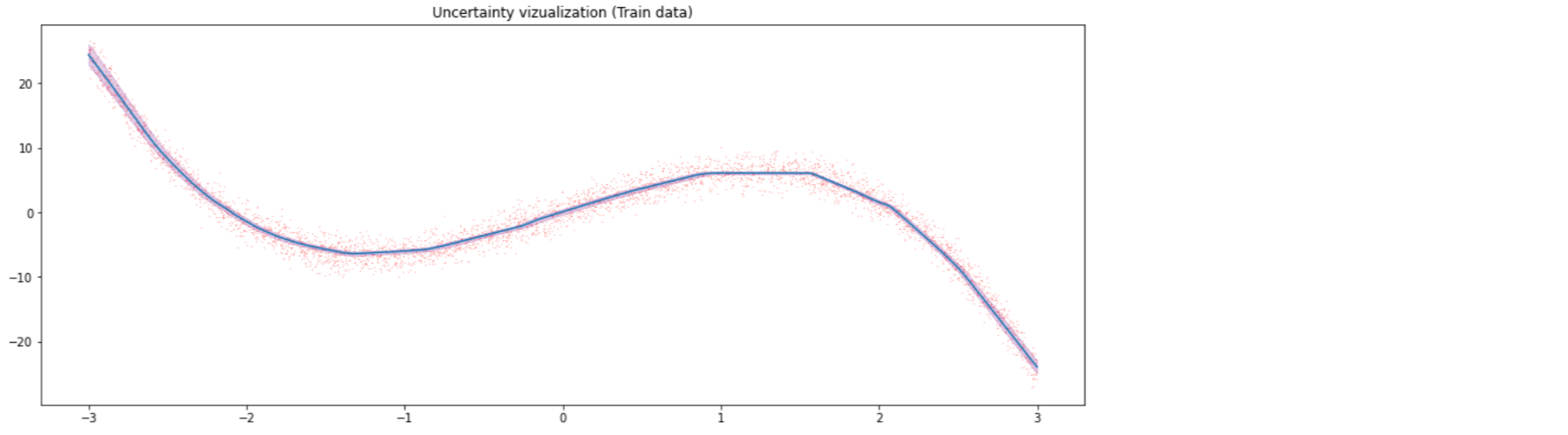
figure2


6-2. Visualization

위 모델은 “Probabilistic”한 deep learning 모델이기 때문에, ouptut값은 deterministic하지 않다.

이를(feed forward) 1000번 반복하여, 각 data당 1000개의 결과값을 출력하여 저장한다.

Train data

with torch.no_grad():
    trace = np.array([bbb(x_train).detach().cpu().flatten().numpy() for _ in range(1000)]).T
q_25, q_95 = np.quantile(trace, [0.05, 0.95], axis=1)
plt.figure(figsize=(16, 6))
plt.plot(x_train.detach().cpu(), trace.mean(1))
plt.title('Uncertainty vizualization (Train data)')
plt.scatter(x_train.detach().cpu(), y_train.detach().cpu(),s=0.01,color='red')
plt.fill_between(x_train.detach().cpu().flatten(), q_25, q_95, alpha=0.2,color='purple')

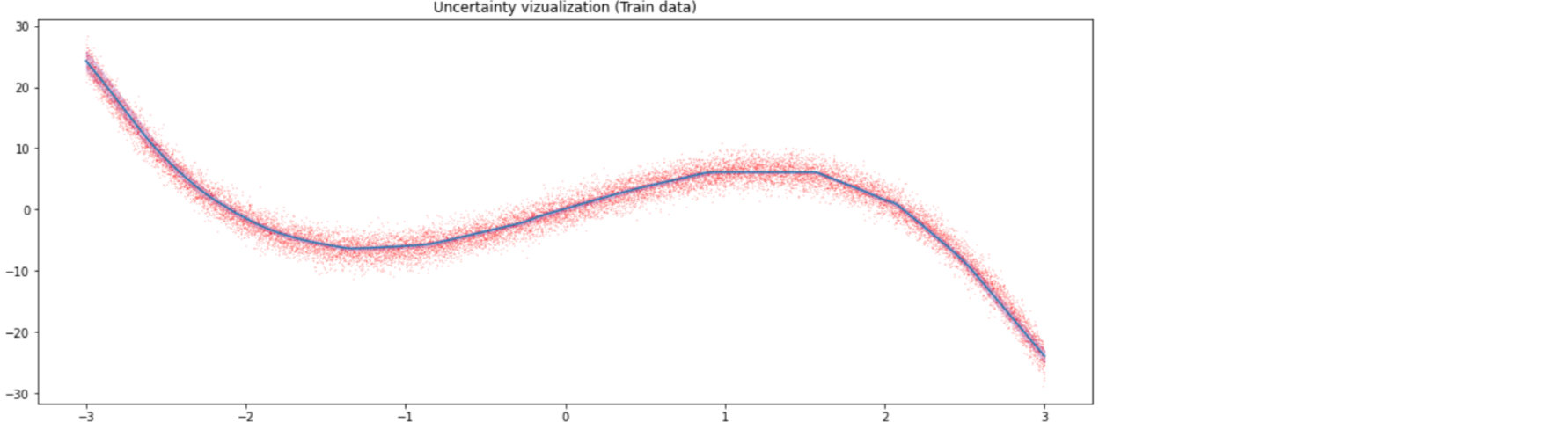
figure2


Validation data

with torch.no_grad():
    trace = np.array([bbb(x_val).detach().cpu().flatten().numpy() for _ in range(1000)]).T
q_25, q_95 = np.quantile(trace, [0.05, 0.95], axis=1)
plt.figure(figsize=(16, 6))
plt.plot(x_val.detach().cpu(), trace.mean(1))
plt.title('Uncertainty vizualization (Train data)')
plt.scatter(x_val.detach().cpu(), y_val.detach().cpu(),s=0.01,color='red')
plt.fill_between(x_val.detach().cpu().flatten(), q_25, q_95, alpha=0.2,color='purple')

figure2

You May Also Enjoy

less than 1 minute read

2 minute read

4 minute read

1 minute read