(Pytorch) 04.Deep Ensembles

Deep Ensembles

( 이론 참고 : https://seunghan96.github.io/bnn/14.Simple-and-Scalable-Predictive-Uncertainty-Estimation-using-Deep-Ensembles-(2017)/ )

( 코드 참고 : https://github.com/cpark321/uncertainty-deep-learning/ )

1. Import Packages

import numpy as np
from matplotlib import pyplot as plt
import seaborn as sns
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

2. Make Sample Dataset

(1) 임의의 가상 dataset을 만든다 ( n =10000 )

• Y_real : \(f(x)\)
• Y_noise : \(f(x)\) + \(\epsilon\), where \(\epsilon \sim N(0,1.5^2)\)

def func(x):
    return 0.2*np.power(x, 3)-2*np.power(x, 2+1)+8*x

n=10000
sigma=1.5

X = np.linspace(-3, 3, n)
Y_real = func(X)
Y_noise = (Y_real+np.random.normal(0,sigma,n))

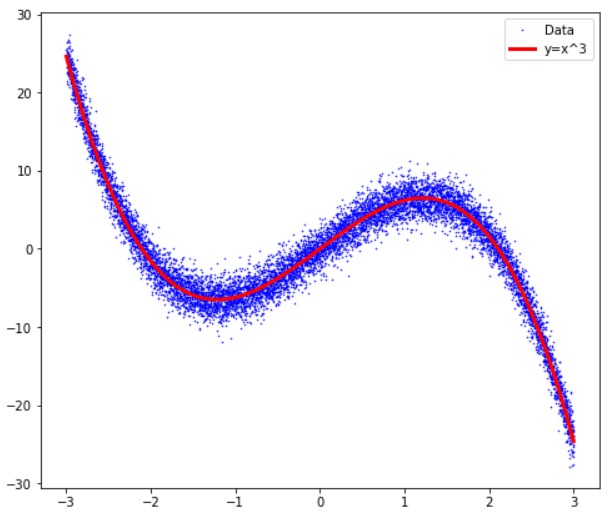
(2) data의 분포

plt.rcParams['figure.figsize'] = [8, 7]
plt.plot(X, Y_noise, '.', markersize=1, color='blue')
plt.plot(X, Y_real, 'r', linewidth=3)
plt.legend(['Data', 'y=x^3'], loc = 'best')
plt.show()

(3) 형태 변환

• tensor 형태로 변환
• shape 변경

X = torch.tensor(X,dtype=torch.float64).view(-1,1)
Y_real = torch.tensor(Y_real,dtype=torch.float64).view(-1,1)
Y_noise = torch.tensor(Y_noise,dtype=torch.float64).view(-1,1)

3. Define our Loss function

Negative Log Likelihood ( Gaussian)

\[-\frac{N}{2} \log \left(2 \pi \sigma^{2}\right)-\frac{1}{2 \sigma^{2}} \sum_{n=1}^{N}\left(x_{n}-\mu\right)^{2}\]

def CustomLoss(y_pred,y_real,sigma):
  gauss_loss = torch.mean(0.5*torch.log(sigma**2) + 0.5*torch.div(torch.square(y_real - y_pred), sigma)) + 1e-6
  return gauss_loss

4. Modeling

• 4-1 ) Gaussian Layer : GaussianLayer
• 4-2 ) Network using Gaussian Layer : SSDE

4-1. Gaussian Layer : GaussianLayer

Parameter 소개

• w_mu, w_sigma, b_mu, b_sigma : weight와 bias의 mu & sigma
• layer_mu : mu를 출력하는 함수 (layer)
• layer_sigma : sigma를 출력하는 함수 (layer)

Input : X

output : mu와 sigma

class GaussianLayer(nn.Module):
  def __init__(self,inter_dim,output_dim):
    super(GaussianLayer, self).__init__()
    self.inter_dim = inter_dim
    self.output_dim = output_dim
    self.w_mu = nn.Parameter(torch.ones(self.inter_dim,self.output_dim))
    self.w_sigma = nn.Parameter(torch.ones(self.inter_dim,self.output_dim))
    self.b_mu = nn.Parameter(torch.ones(1,self.output_dim))
    self.b_sigma = nn.Parameter(torch.ones(1,self.output_dim))
    self.layer_mu = nn.Linear(self.inter_dim,self.inter_dim)
    self.layer_sigma = nn.Linear(self.inter_dim,self.inter_dim)

  def forward(self,x):
    mu_pred = self.layer_mu(x)
    sigma_pred = self.layer_sigma(x)
    mu_pred = torch.matmul(mu_pred,self.w_mu)+self.b_mu
    sigma_pred = torch.matmul(sigma_pred,self.w_sigma)+self.b_sigma
    sigma_pred = torch.log(1+sigma_pred)+ 1e-06
    return [mu_pred,sigma_pred]

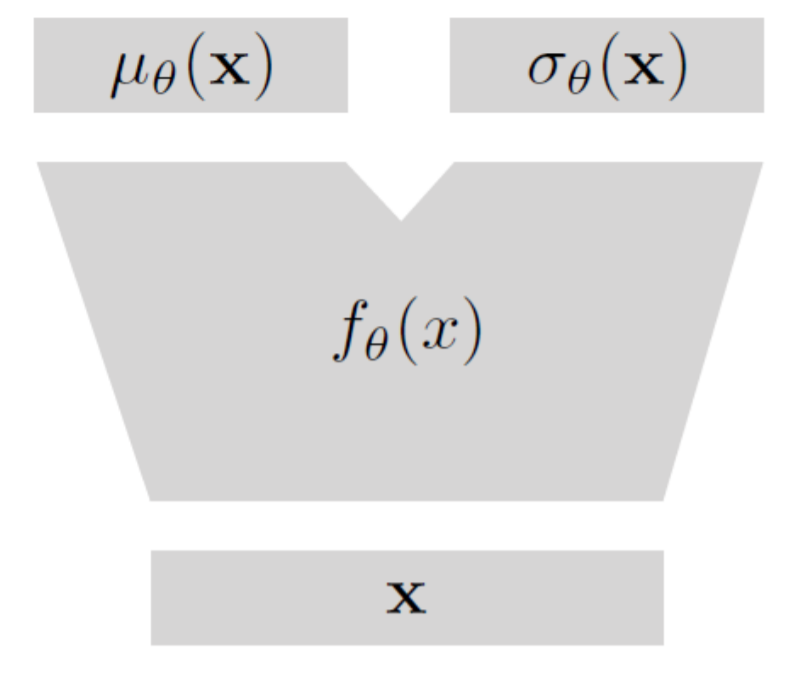
4-2. Network using Gaussian Layer : SSDE

두개의 hidden layer를 통과한 이후,

Gaussian Layer를 통해 mu와 sigma를 출력한다

class SSDE(nn.Module):
  def __init__(self,input_dim,inter_dim,output_dim):
    super(SSDE, self).__init__()
    self.input_dim = input_dim
    self.inter_dim = inter_dim
    self.output_dim = output_dim
    self.layer1 = nn.Linear(self.input_dim,10)
    self.layer2 = nn.Linear(10,self.inter_dim)
    self.GaussianLayer = GaussianLayer(self.inter_dim,self.output_dim)

  def forward(self,x):
    x =  self.layer1(x.float())
    x = nn.ReLU()(x)
    x =  self.layer2(x)
    x = nn.ReLU()(x)
    xs =  self.GaussianLayer(x)
    mu,sigma = xs
    return mu,sigma

5. Train Model

차원 설정

input_dim = 1
inter_dim = 30
output_dim = 1

epoch 수 설정 & train/test split

n_epoch=1000
val_idx = np.random.choice(n, int(n*0.2),replace=False)
train_idx = np.array(list(set(np.arange(n))-set(val_idx)))
x_train,x_val = X[train_idx],X[val_idx]
y_train,y_val = Y_noise[train_idx],Y_noise[val_idx]

train 함수

def train(n_epoch,opt,x_train,y_train,x_val,y_val):
  for epoch in range(1,n_epoch+1):
    mu_pred,sigma_pred = model(x_train)
    train_loss = CustomLoss(mu_pred,y_train,sigma_pred)
    val_mu_pred,val_sigma_pred = model(x_val)
    val_loss = CustomLoss(val_mu_pred,y_val,val_sigma_pred)

    opt.zero_grad()
    train_loss.backward()
    opt.step()

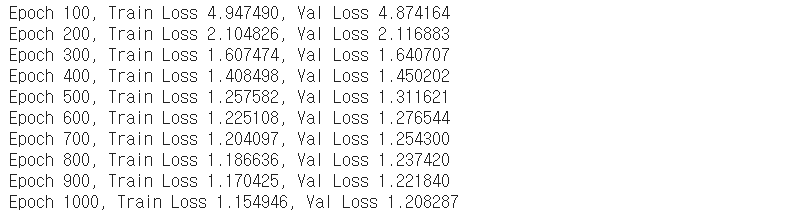
    if epoch%50==0:
      print('Epoch %d, Train Loss %f, Val Loss %f' %(epoch,float(train_loss),float(val_loss)))

모델을 학습시킨다

• optimizer : Adam

6. Result

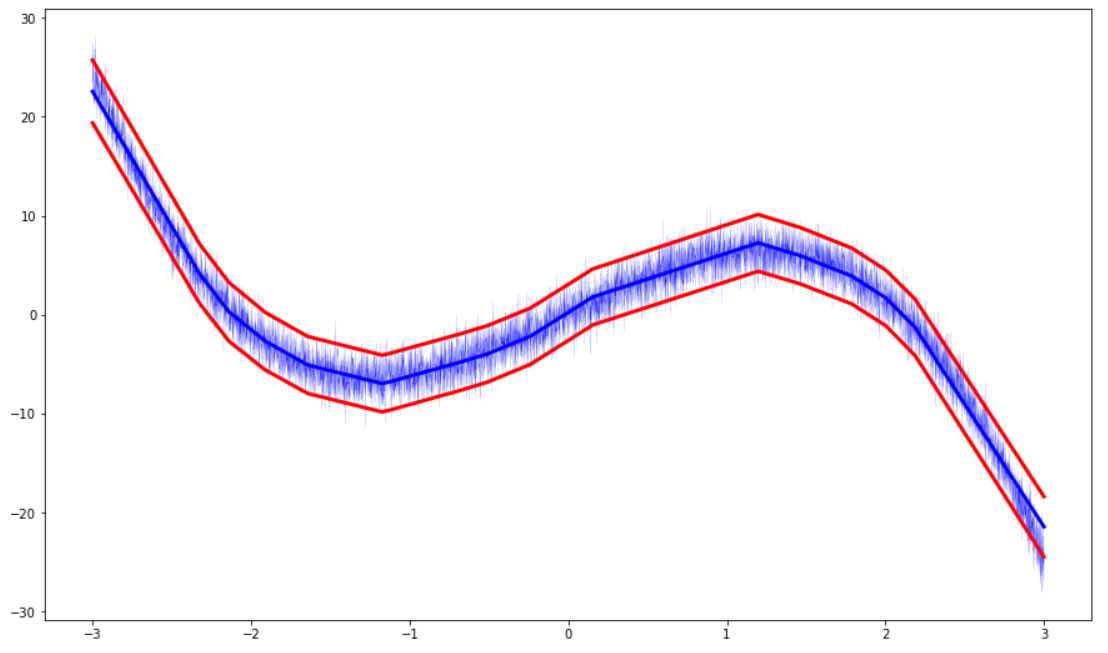
총 1000개의 (mu,sigma) pair 완성

mu_result,sigma_result = model(X)

Visualization

plt.figure(1, figsize=(15, 9))
plt.plot([i[0] for i in X], [i for i in Y_noise], 'b', linewidth=0.1)
plt.plot([i[0] for i in X], [i for i in mu_result], 'b', linewidth=3)
upper = [i+k for i,k in zip(mu_result,sigma_result)]
lower = [i-k for i,k in zip(mu_result, sigma_result)]
plt.plot([i[0] for i in X], [i for i in upper], 'r', linewidth =3)
plt.plot([i[0] for i in X], [i for i in lower], 'r', linewidth = 3)
plt.show()