(paper 11) With a Little Help from My Friends; Nearest-Neighbor Contrastive Learning of Visual Representations

With a Little Help from My Friends: Nearest-Neighbor Contrastive Learning of Visual Representations

Contents

1. Abstract
2. Related Work
3. Approach
   1. Contrastive Instance Discrimination
   2. Nearest-Neighbor CLR (NNCLR)
   3. Implementation Details

0. Abstract

Use positive samples from OTHER instances in the dataset

propose NNCLR

• samples the nearest neighbors from the dataset in the latent space & treat them as positives

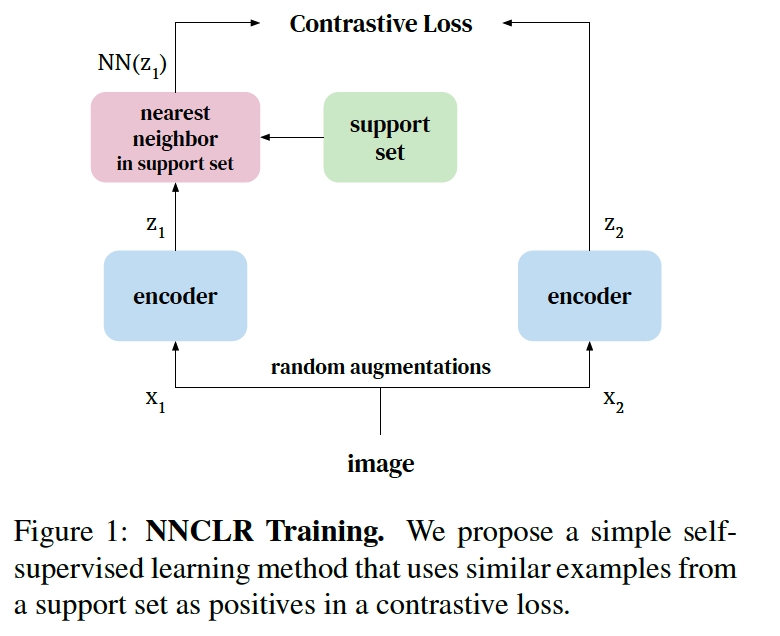
1. Related Work

Queues and Memory Banks

use a SUPPORT set as memory during training

( similar to MoCO )

MoCo vs NNCLR

• [MoCo] uses elements of the queue as NEGATIVES
• [NNCLR] ~ POSITIVES

2. Approach

describe contrastive learning in the context of

• (1) instance discrimination
• (2) SimCLR

(1) Contrastive Instance Discrimination

InfoNCE

\(\mathcal{L}_{i}^{\text {InfoNCE }}=-\log \frac{\exp \left(z_{i} \cdot z_{i}^{+} / \tau\right)}{\exp \left(z_{i} \cdot z_{i}^{+} / \tau\right)+\sum_{z^{-} \in \mathcal{N}_{i}} \exp \left(z_{i} \cdot z^{-} / \tau\right)}\).

SimCLR

uses 2 views of same image as positive pair

Given mini-batch of images \(\left\{x_{1}, x_{2} \ldots, x_{n}\right\}\),

\(\rightarrow\) 2 different augmentations (views) are generated

• (1) \(z_{i}=\phi\left(\operatorname{aug}\left(x_{i}\right)\right)\)
• (2) \(z_{i}^{+}=\phi\left(\operatorname{aug}\left(x_{i}\right)\right)\)

InfoNCE loss used in SimCLR : \(\mathcal{L}_{i}^{\text {SimCLR }}=-\log \frac{\exp \left(z_{i} \cdot z_{i}^{+} / \tau\right)}{\sum_{k=1}^{n} \exp \left(z_{i} \cdot z_{k}^{+} / \tau\right)}\)

• each embedding is \(l_{2}\) normalized before the dot product is computed in the loss

(2) Nearest-Neighbor CLR (NNCLR)

propose using \(z_{i}\) ‘s NN in the support set \(Q\) to form the positive pair

• \(\mathcal{L}_{i}^{\mathrm{NNCLR}}=-\log \frac{\exp \left(\mathrm{NN}\left(z_{i}, Q\right) \cdot z_{i}^{+} / \tau\right)}{\sum_{k=1}^{n} \exp \left(\mathrm{NN}\left(z_{i}, Q\right) \cdot z_{k}^{+} / \tau\right)}\).
  • where \(\mathbf{N N}(z, Q)=\underset{q \in Q}{\arg \min } \mid \mid z-q \mid \mid _{2}\)

(3) Implementation Details

(1) symmetric loss

• add \(-\log \left(\exp \left(\mathrm{NN}\left(z_{i}, Q\right) \cdot z_{i}^{+} / \tau\right) / \sum_{k=1}^{n} \exp \left(\mathrm{NN}\left(z_{k}, Q\right) \cdot z_{i}^{+} / \tau\right)\right.\)

(2) insipred by BYOL …

• pass \(z_{i}^{+}\)through a prediction head \(g\) to produce embeddings \(p_{i}^{+}=g\left(z_{i}^{+}\right)\).
• then use \(p_{i}^{+}\)instead of \(z_{i}^{+}\)in \(\mathcal{L}_{i}^{\mathrm{NNCLR}}=-\log \frac{\exp \left(\mathrm{NN}\left(z_{i}, Q\right) \cdot z_{i}^{+} / \tau\right)}{\sum_{k=1}^{n} \exp \left(\mathrm{NN}\left(z_{i}, Q\right) \cdot z_{k}^{+} / \tau\right)}\).

Support Set

implement support set as queue

• dimension : \([m, d]\)
  • \(m\) : size of queue
  • \(d\) : size of embeddingsRandAugment