(paper 13) TeachAugment

TeachAugment : Data Augmentation Optimization using Teacher Knowledge

Contents

1. Abstract
2. Introduction
3. Related Work
4. Data Augmentation Optimization using teacher knowledge
   1. Preliminaries
   2. TeachAugment
   3. Improvement Techniques
5. Data Augmentation using NN

0. Abstract

Adversarial Data Augmentation strategies :

• search augmentation, maximizing task loss
• show improvement in model generalization

\(\rightarrow\) but require careful parameter tunining

TeachAugment

• propose a DA optimization method based on adversarial strategy

• without requiring careful tuning, by leveraging a teacher model

1. Introduction

AutoAugment : requires thousands of GPU

Online DA optimization

• alternately update (1) augmentation policies & (2) target network
• Advantages
  • a) reduce computational costs
  • b) simplify the DA pipeline

• mostly based on adversarial strategy

  • searches augmentation by maximizing task loss for target model

    ( = improve model generalization )

  • problem : unstable

    • maximizing loss = can be achieved by collapsing the inherent images

    • to avoid collapse ….. regularize augmentation based on prior knowledge

      \(\rightarrow\) need lots of tuned parameters!

To alleviate tuning problem …. propose TeachAugment

• online DA optimization using teacher knowledge
• based on adversarial DA strategy
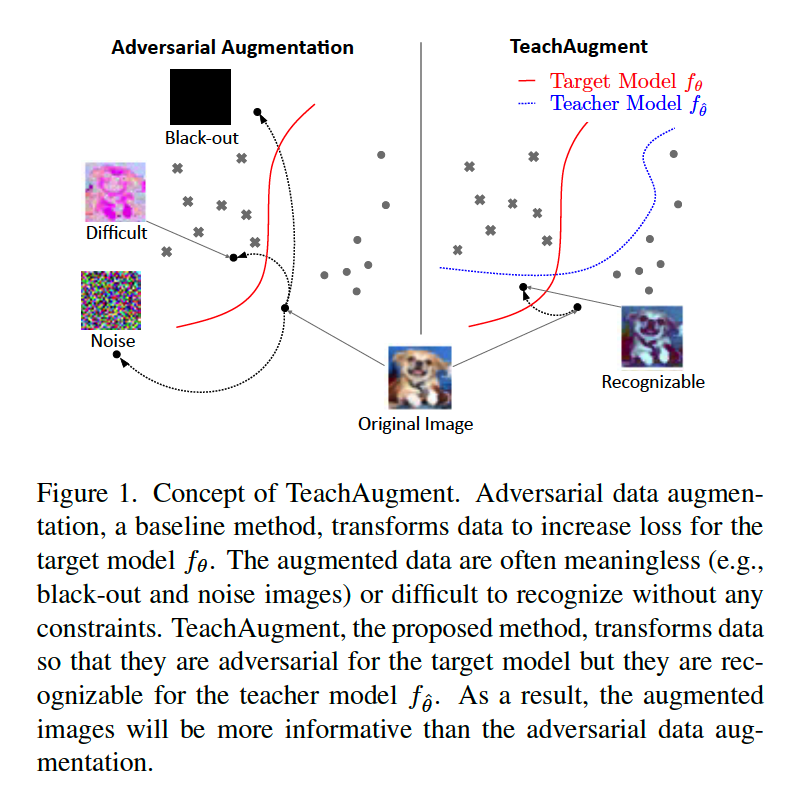
• search augmentation where transformed image is RECOGNIZABLE for a TEACHER MODEL
• do not require priors / hyperparameters

Propose DA using NN that represent 2 functions

• (1) geometric augmentation

• (2) color augmentation

• why NN?
  • a) update using GD
  • B) reduce # of functions in the search space to “2”

Contributions

1. online DA ( w.o careful parameter tuning )
2. DA using NN

2. Related Work

Conventional DA :

• geometric & color transformation are widely used!

• using DA, improvements are made on…

  • (1) image recognition accuracy
  • (2) un/semi-supervised representation learning

• usually improves model generalization,

  but sometimes hurts performance, or induce unexpected biases

  \(\rightarrow\) need to find effective augmentation policies

ex) AutoAugment

\(\rightarrow\) automatically search for effective data augmentation

Data Augmentation search

• category 1) proxy task based
• category 2) proxy task free

Proxy Task based

• search DA strategies on proxy tasks, that uses subsets of data and/or small models to reduce computational costs
• thus, might be SUB-OPTIMAL

Proxy Task free

• DIRECTLY search DA strategies on the target network with all data

• thus, potentially OPTIMAL

• Ex) RandAugment, Trivial Augment

  • randomize the parameters search & reduce the size of search space

• Ex) Adversarial AutoAugment, PointAugment

  • update augmentation policies in an online manner

    ( = alternately update target network & augmentation policies )

This paper focus on PROXY TASK FREE methods , updating policies in an ONLINE manner

• reason 1) can directly search DA strategies on target network with all data
• reason 2) unify the search & training process

3. Data Augmentation Optimization using teacher knowledge

(1) Preliminaries

Notation

• dataset : \(x \sim \mathcal{X}\)

• \(a_{\phi}\) : augmentation function, parameterized by \(\phi\)
• \(f_\theta\) : target network
  • fed into target network : \(f_{\theta}\left(a_{\phi}(x)\right)\)

Training procedure : \(\min _{\theta} \mathbb{E}_{x \sim \mathcal{X}} L\left(f_{\theta}\left(a_{\phi}(x)\right)\right.\).

( Adversarial DA : searches \(\phi\), maximizing the loss )

\(\rightarrow\) \(\max _{\phi} \min _{\theta} \mathbb{E}_{x \sim \mathcal{X}} L\left(f_{\theta}\left(a_{\phi}(x)\right)\right.\)

• alternately updating \(\phi\) & \(\theta\)

PROBLEM?

maximizing the loss, w.r.t \(\phi\) can be just obtained by collapsing the inherent meanings of \(x\)

\(\rightarrow\) solution : utilize teacher model to avoid the collapse !

(2) TeachAugment

Notation :

• \(f_{\hat{\theta}}\) : teacher model
• \(f_{\theta}\) : target model

Suggest 2 types of teacher model

• (1) pre-trained teacher

• (2) EMA teacher

  ( = weights are updated as an exponential moving average of target model’s weights )

Proposed Objective :

• \(\max _{\phi} \min _{\theta} \mathbb{E}_{x \sim \mathcal{X}}\left[L\left(f_{\theta}\left(a_{\phi}(x)\right)\right)-L\left(f_{\hat{\theta}}\left(a_{\phi}(x)\right)\right)\right]\).

  • maximize for TARGET model
  • minimize for TEACHER model

• avoids collapsing the inherent meanings of images

  ( \(\because\) if not, loss for TEACHER model will explode!! )

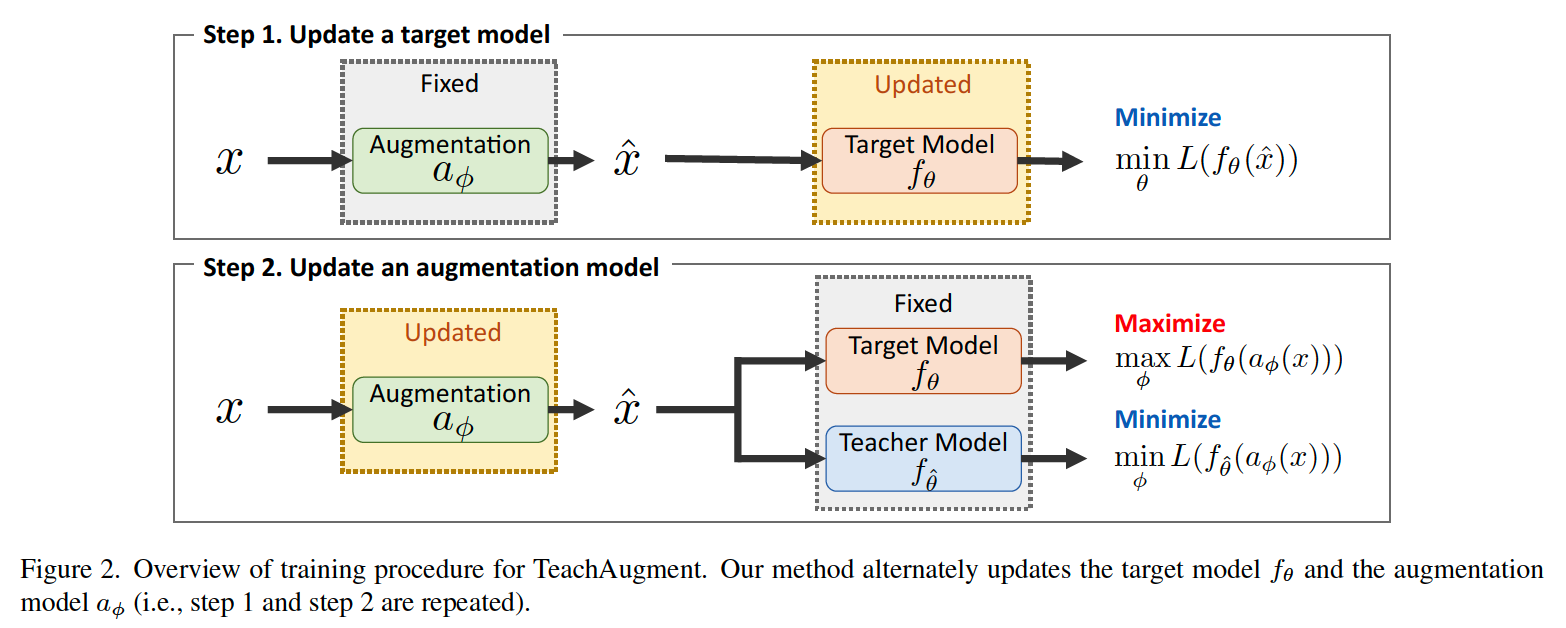
• objective is solved by *ALTERNATIVELY updating the augmentation function & target model
• process
  • step 1) update TARGET network for \(n_{inner}\) steps
  • step 2) update AUGMENTATION function

(3) Improvement Techniques

training procedure : similar to GANs & actor-critic in RL

( lots of strategies to mitigate instabilities & improve training )

4. Data Augmentation using NN

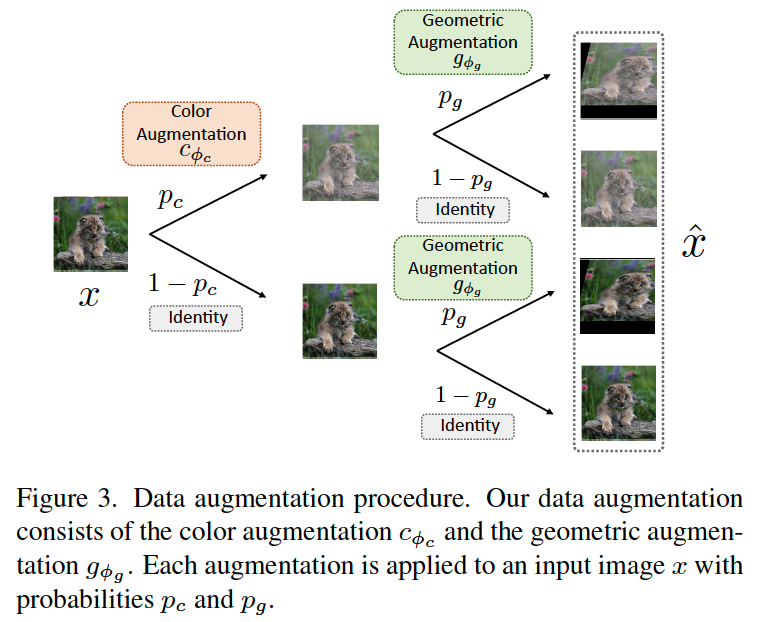
Two NNs

• (1) color augmentation model : \(c_{\phi_{c}}\)
• (2) geometric augmentation model : \(g_{\phi_{g}}\)
• (1) + (2) = \(a_{\phi}=g_{\phi_{g}} \circ c_{\phi_{c}}\)
  • parameters : \(\phi=\left\{\phi_{c}, \phi_{g}\right\}\)

• input image : \(x \in \mathbb{R}^{M \times 3}\)

  ( \(M\) : number of pixels )

• data augmentation probability

  • color : \(p_{c} \in(0,1)\)
  • gemoetric : \(p_{g} \in(0,1)\)

Data Augmentation

• [ color ] \(\tilde{x}_{i}=t\left(\alpha_{i} \odot x_{i}+\beta_{i}\right),\left(\alpha_{i}, \beta_{i}\right)=c_{\phi_{c}}\left(x_{i}, z, c\right)\)
• [ geometric ] \(\hat{x}=\operatorname{Affine}(\tilde{x}, A+I), A=g_{\phi_{g}}(z, c)\)
  • affine transformation of \(\tilde{x}\) with a parameter \(A+I\)
• ( + also learn the probabilities \(p_g\) & \(p_c\) )