AET vs. AED : Unsupervised Representation Learning by Auto-Encoding Transformations rather than Data
Contents
- Abstract
- AET : The Proposed Approach
- The Formulation
- The AET Family
0. Abstract
AET ( Auto Encoding Transformation )
-
novel paradigm of unsupervised representation learning
-
given randomly sampled transformation, AET seeks to predict it
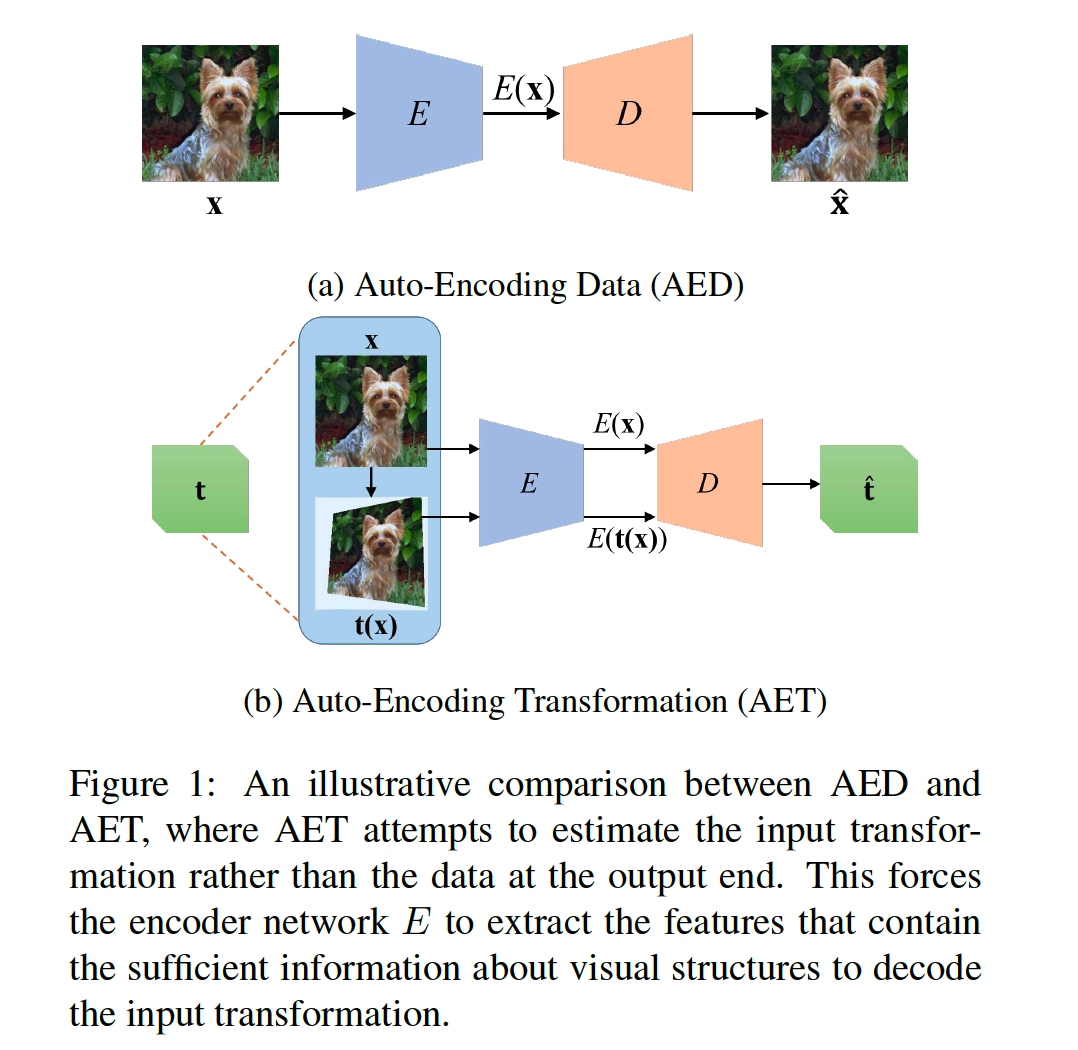
1. AET : The Proposed Approach
(1) formulation of AET
(2) instantiate AET with different genres of transformations
(1) The Formulation
Sample …
- a transformation \(t \sim \mathcal{T}\)
- an image : \(\mathbf{x} \sim \mathcal{X}\)
\(\rightarrow\) transform an image \(\mathrm{t}(\mathrm{x})\)
Goal : learn an encoder & decoder
-
encoder : \(E: \mathbf{x} \mapsto E(\mathbf{x})\)
- extract the representation \(E(\mathbf{x})\) for a sample \(\mathrm{x}\)
-
decoder : \([E(\mathbf{x}), E(\mathbf{t}(\mathbf{x}))] \mapsto \hat{\mathbf{t}}\)
-
gives an estimate \(\hat{\mathbf{t}}\) of input transformation,
by decoding from the encoded representations of original **and **transformed images
-
problem of AET
= jointly traning the feature encoder \(E\) & transformation decoder \(D\)
- \(\min _{E, D} \underset{\mathbf{t} \sim \mathcal{T}, \mathbf{x} \sim \mathcal{X}}{\mathbb{E}} \ell(\mathbf{t}, \hat{\mathbf{t}})\).
- where \(\hat{\mathbf{t}}=D[E(\mathbf{x}), E(\mathbf{t}(\mathbf{x}))]\)
(2) The AET Family
3 genres
- (1) parameterized
- (2) GAN-induced
- (3) non-parameterized
Parameterized Transformations
family of transformations \(\mathcal{T}=\left\{\mathbf{t}_{\boldsymbol{\theta}} \mid \boldsymbol{\theta} \sim \boldsymbol{\Theta}\right\}\)
- parameters \(\boldsymbol{\theta}\) sampled from a distribution \(\Theta\)
transformations, such as affine and projective transformations,
can be represented by a parameterized matrix \(M(\boldsymbol{\theta}) \in \mathbb{R}^{3 \times 3}\)
Loss function : \(\ell\left(\mathbf{t}_{\boldsymbol{\theta}}, \mathbf{t}_{\hat{\boldsymbol{\theta}}}\right)=\frac{1}{2} \mid \mid M(\boldsymbol{\theta})-M(\hat{\boldsymbol{\theta}}) \mid \mid _{2}^{2}\).
GAN-induced Transformations
local generator \(G(\mathbf{x}, \mathbf{z})\)
- learned with a sampled random noise \(\mathbf{z}\) that parameterizes the underlying transformation around a given image \(\mathbf{x}\).
- \(\mathbf{t}_{\mathbf{z}}(\mathbf{x})=G(\mathbf{x}, \mathbf{z})\).
Loss function : \(\ell\left(\mathbf{t}_{\mathbf{z}}, \mathbf{t}_{\hat{\mathbf{z}}}\right)=\frac{1}{2} \mid \mid \mathbf{z}-\hat{\mathbf{z}} \mid \mid _{2}^{2}\)
Non-parameterized Transformations
just by measuring. The avverage difference between the transformations of randomly sampled images!
Loss function : \(\ell(\mathbf{t}, \hat{\mathbf{t}})=\underset{\mathbf{x} \sim \mathcal{X}}{\mathbb{E}} \operatorname{dist}(\mathbf{t}(\mathbf{x}), \hat{\mathbf{t}}(\mathbf{x}))\)
