Deep Clustering for Unsupervised Learning of Visual Features
Contents
- Abstract
- Method
- Preliminaries
- Unsupervised Learning by Clustering
- Avoiding Trivial Solutions
0. Abstract
DeepCluster
-
end-to-end training of visual features
- jointly learns….
- (1) the parameters of NN
- (2) cluster assignments of the resulting features
- iteratively …
- step 1) groups the features with standard clustering algorithm (k-means)
- step 2) use the subsequent assignments as supervision to update NN
1. Method
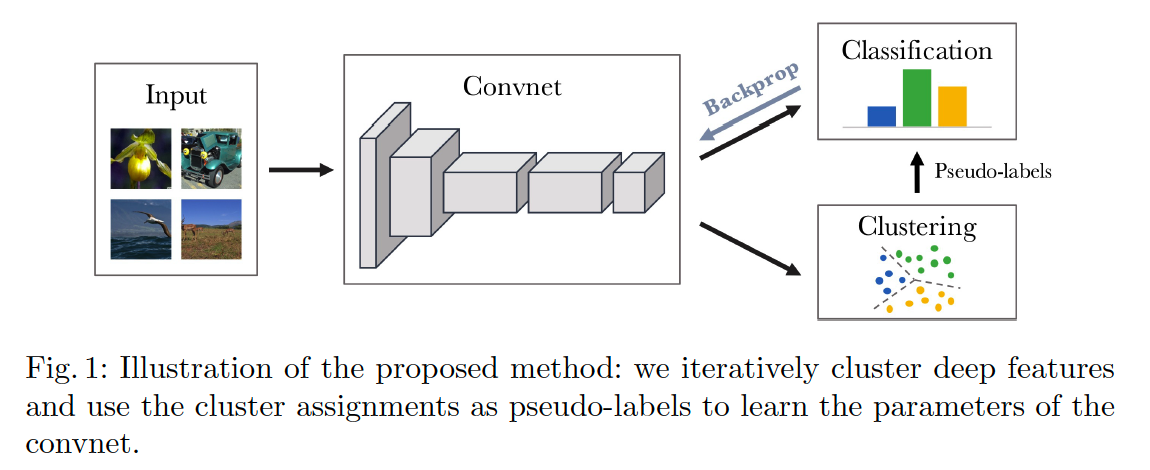
(1) Preliminaries
data : \(X=\left\{x_{1}, x_{2}, \ldots, x_{N}\right\}\)
model :
- (1) convent mapping : \(f_{\theta}\)
- (2) classifier : \(g_{W}\)
Loss function : \(\min _{\theta, W} \frac{1}{N} \sum_{n=1}^{N} \ell\left(g_{W}\left(f_{\theta}\left(x_{n}\right)\right), y_{n}\right)\).
( \(l\) : negative log-softmax )
(2) Unsupervised Learning by Clustering
cluster the output of the convnet &
use the subsequent cluster assignments as “pseudo-labels” to optimize \(\min _{\theta, W} \frac{1}{N} \sum_{n=1}^{N} \ell\left(g_{W}\left(f_{\theta}\left(x_{n}\right)\right), y_{n}\right)\)
( iteratively learns the features & groups them )
K-means
- input : \(f_{\theta}\left(x_{n}\right)\)
-
output : clusters them into \(k\) distinct groups
- jointly learns a ..
- (1) \(d \times k\) centroid matrix \(C\)
- (2) cluster assignments \(y_{n}\) of each image \(n\)
- loss function :
- \(\min _{C \in \mathbb{R}^{d \times k}} \frac{1}{N} \sum_{n=1}^{N} \min _{y_{n} \in\{0,1\}^{k}} \mid \mid f_{\theta}\left(x_{n}\right)-C y_{n} \mid \mid _{2}^{2} \quad \text { such that } y_{n}^{\top} 1_{k}=1\).
\(\rightarrow\) these assignments are used as pseudo-labels
( do not use centroid matrix \(C\) )
problem : degenerating problem
\(\rightarrow\) cluster them into a single group… solution??
(3) Avoiding Trivial Solutions
solutions are typically based on constraining or penalizing the MINIMAL number of points per cluster
but…not applicable to large scale datasets
a) empty clusters
when cluster becomes empty….
randomly select a non-empty cluster & use its centroid with a small perturbation as a new centroid
b) trivial parameterization
minimizing \(\min _{\theta, W} \frac{1}{N} \sum_{n=1}^{N} \ell\left(g_{W}\left(f_{\theta}\left(x_{n}\right)\right), y_{n}\right)\)
\(\rightarrow\) leads to a trivial parameterization
( = predict the same output, regardless of output )
solution ?
-
sample images based on a uniform distn over the classes ( or pseudo labels )
( = weighted loss, with weight of inverse of size of clusters )
