( 참고 : 패스트 캠퍼스 , 한번에 끝내는 컴퓨터비전 초격차 패키지 )
Classical Computer Vision (2)
5. Blob
Blob : 주변보다 밝거나/어두운 지역
Blob Detection 과정
- (1) Smoothing
- (2) LoG ( 혹은 DoG ) 적용
- LoG : Laplacian of Gaussian
- DoG : Difference of Gaussian
- (3) Optimal Scale & Orientation parameter 찾기
(1) Edge Detection 복습
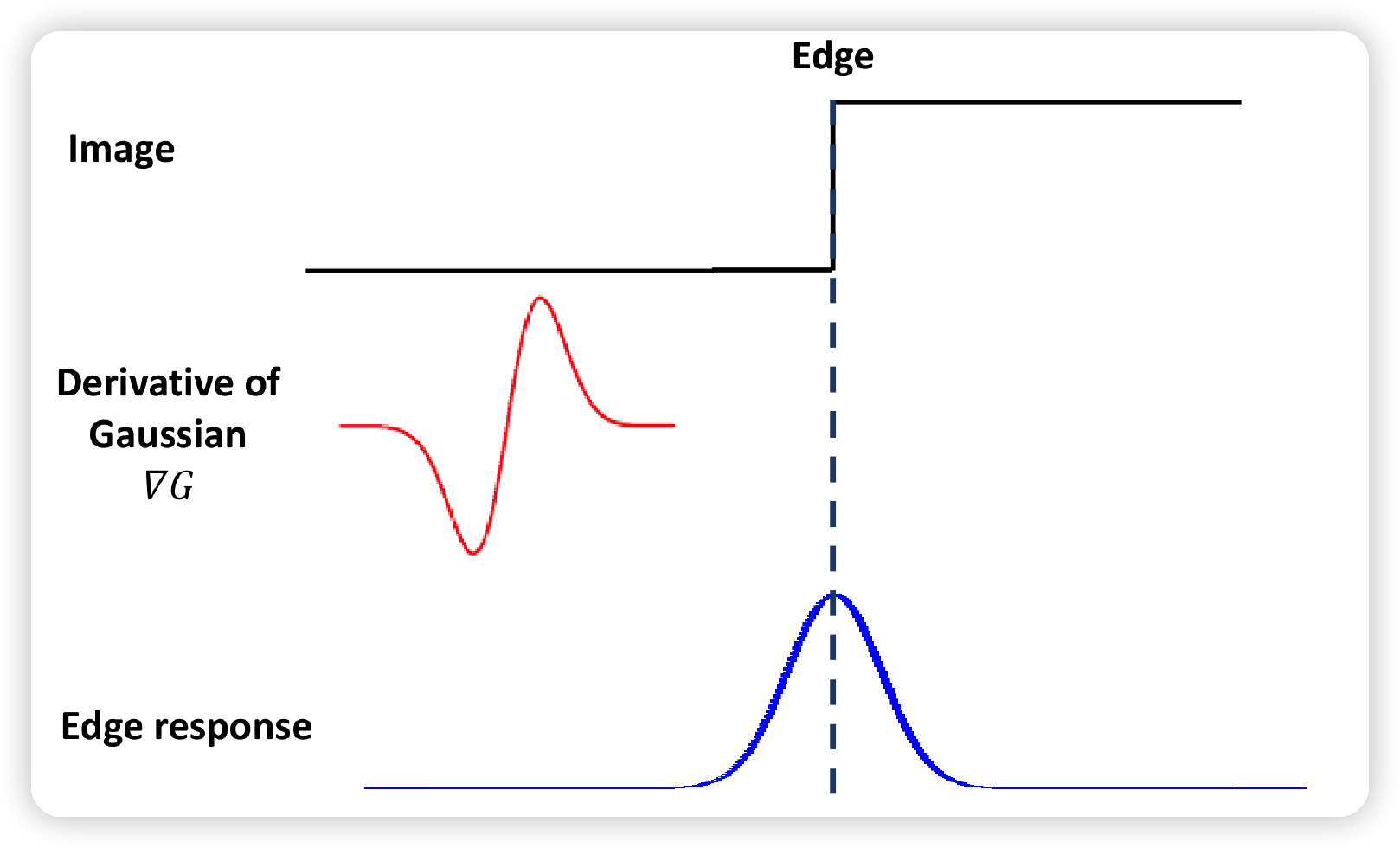
위 그림과 같이 Edge가 있는 이미지에 DoG를 적용하면, 맨 아래와 같은 Edge Response를 얻게 된다.
해당 Edge Response 값이 높은 것을 통해, 우리는 엣지가 있다는 사실을 알 수 있다.
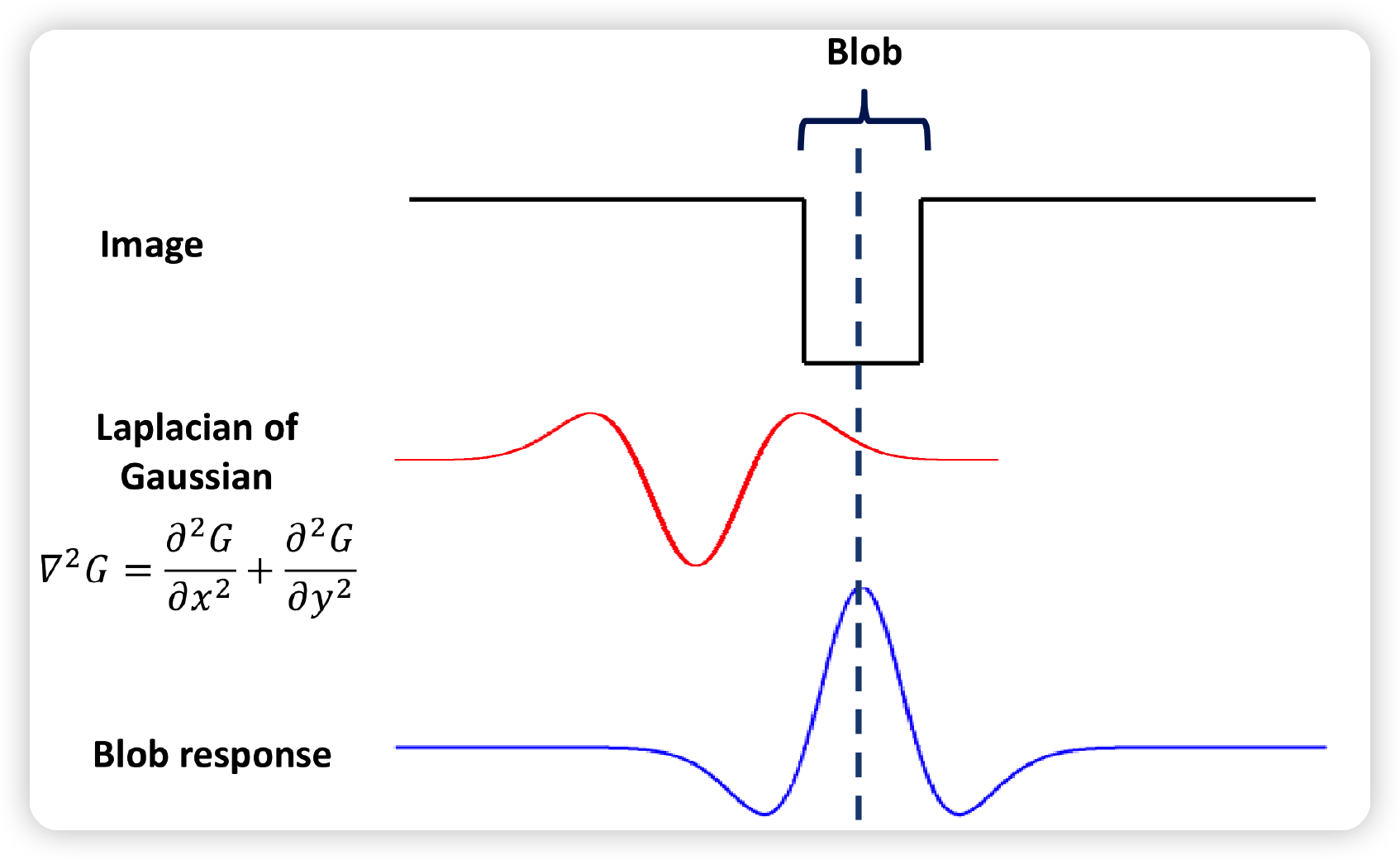
(2) Blob Detection
위와 마찬가지로, Blob가 있는 이미지에 LoG를 적용하면, 다음과 같다.
(3) Laplace of Gaussian (LoG)
Laplace Operator = 2개의 gradient vector의 내적
ex) N차원의 2개의 벡터라면..
- \(\nabla^{2}=\left[\begin{array}{lll} \frac{\partial}{\partial x_{1}} & \ldots & \frac{\partial}{\partial x_{N}} \end{array}\right]\left[\begin{array}{lll} \frac{\partial}{\partial x_{1}} & \ldots & \frac{\partial}{\partial x_{N}} \end{array}\right]^{\top}=\sum_{n=1}^{N} \frac{\partial}{\partial x_{n}}\).
ex) 이미지와 같이 2차원 ( x,y )의 벡터 2개라면..
- \(\nabla^{2}=\left[\begin{array}{ll} \frac{\partial}{\partial x} & \frac{\partial}{\partial y} \end{array}\right]\left[\begin{array}{ll} \frac{\partial}{\partial x} & \frac{\partial}{\partial y} \end{array}\right]^{\top}=\frac{\partial^{2}}{\partial x^{2}}+\frac{\partial^{2}}{\partial y^{2}}\).
2d isotropic Gaussian distn
- isotropic ( 등분산 ) : \(\Sigma=\sigma^{2} \cdot I\)
- 2개의 isotropic Gaussian의 곱 : \(G(x, y, \sigma)=\frac{1}{2 \pi \sigma^{2}} \exp \left(-\frac{x^{2}+y^{2}}{2 \sigma^{2}}\right)\).
Laplacian of “2개의 isotropic Gaussian”
( = Laplacian of Gaussian filter )
\(\begin{aligned} \nabla^{2} G(x, y, \sigma)&=\frac{\partial^{2} G}{\partial x^{2}}+\frac{\partial^{2} G}{\partial y^{2}} \\ &=\frac{x^{2}-\sigma^{2}}{\sigma^{4} \cdot 2 \pi \sigma^{2}} \exp \left(-\frac{x^{2}+y^{2}}{2 \sigma^{2}}\right)+\frac{y^{2}-\sigma^{2}}{\sigma^{4} \cdot 2 \pi \sigma^{2}} \exp \left(-\frac{x^{2}+y^{2}}{2 \sigma^{2}}\right) \\ &=\frac{x^{2}+y^{2}-2 \sigma^{2}}{\sigma^{4} \cdot 2 \pi \sigma^{2}} \exp \left(-\frac{x^{2}+y^{2}}{2 \sigma^{2}}\right)\\&=\frac{x^{2}+y^{2}-2 \sigma^{2}}{\sigma^{4}} G(x, y, \sigma) \end{aligned}\).
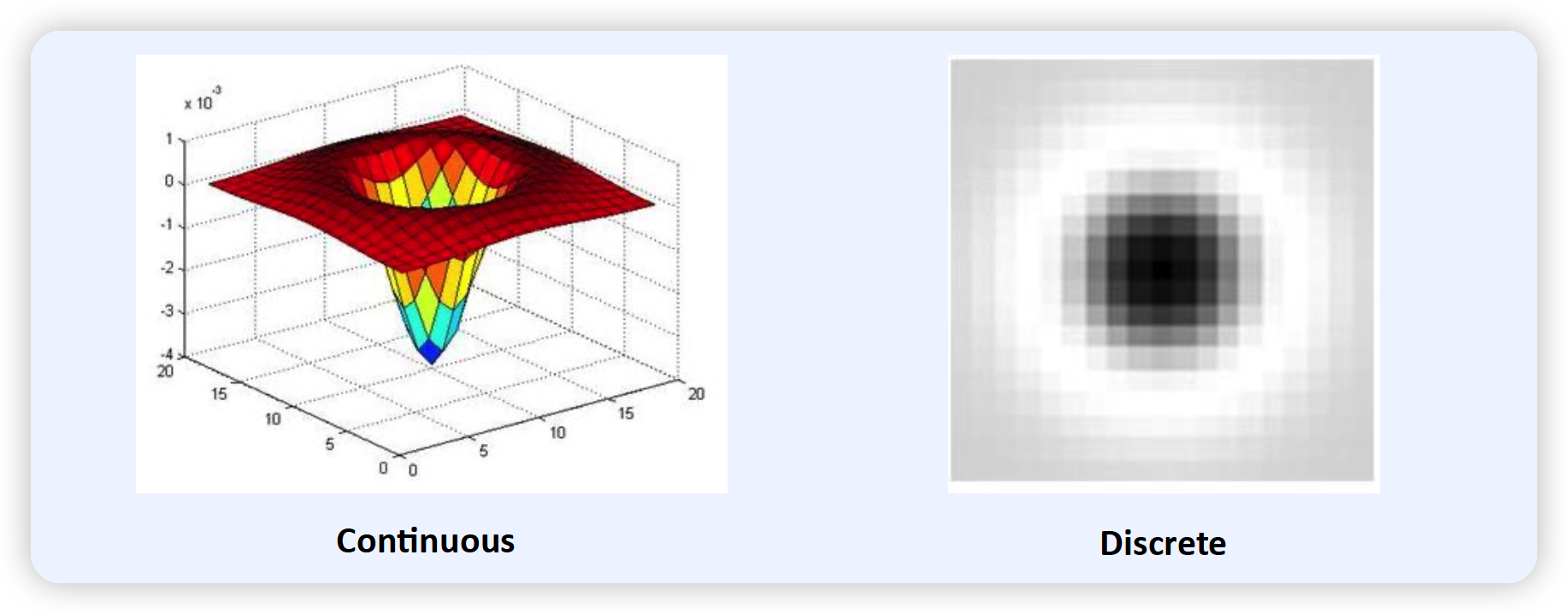
다양한 크기의 Blob에 대한 Laplacian
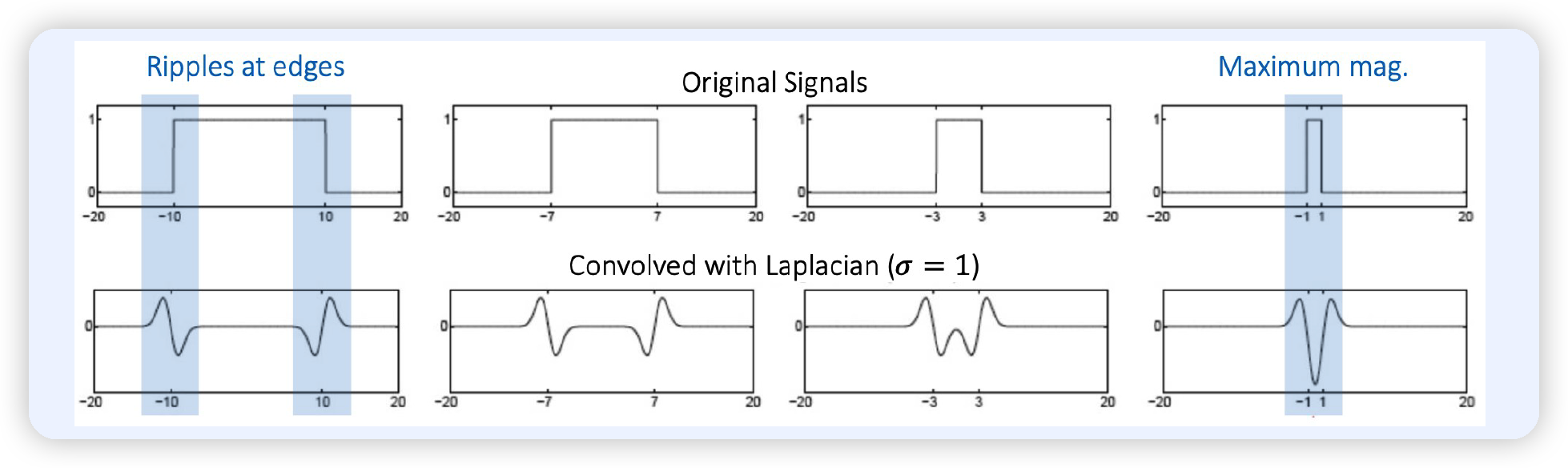
- blob의 center에서 Laplacian값이 제일 커진다,
- Blob의 크기에 따라 optimal scale이 다르다.
(4) Scale Selection & Scale Normalization
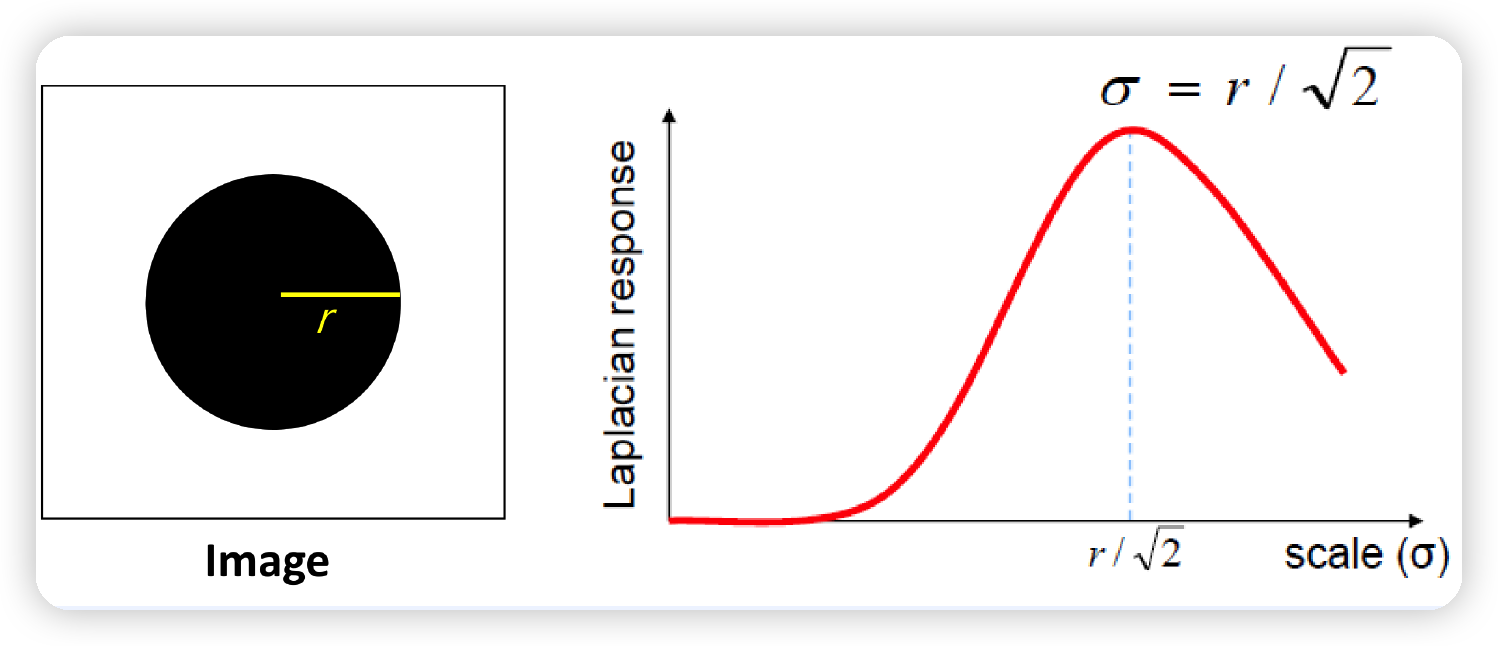
위에서 Optimal scale이라고 했는데, 어떤 scale이 과연 좋을까?
( 즉, \(\sigma\) 값을 어떻게 정할까? )
\(\rightarrow\) \(\sigma = r/\sqrt2\) , where \(r\)= radius of binary circle
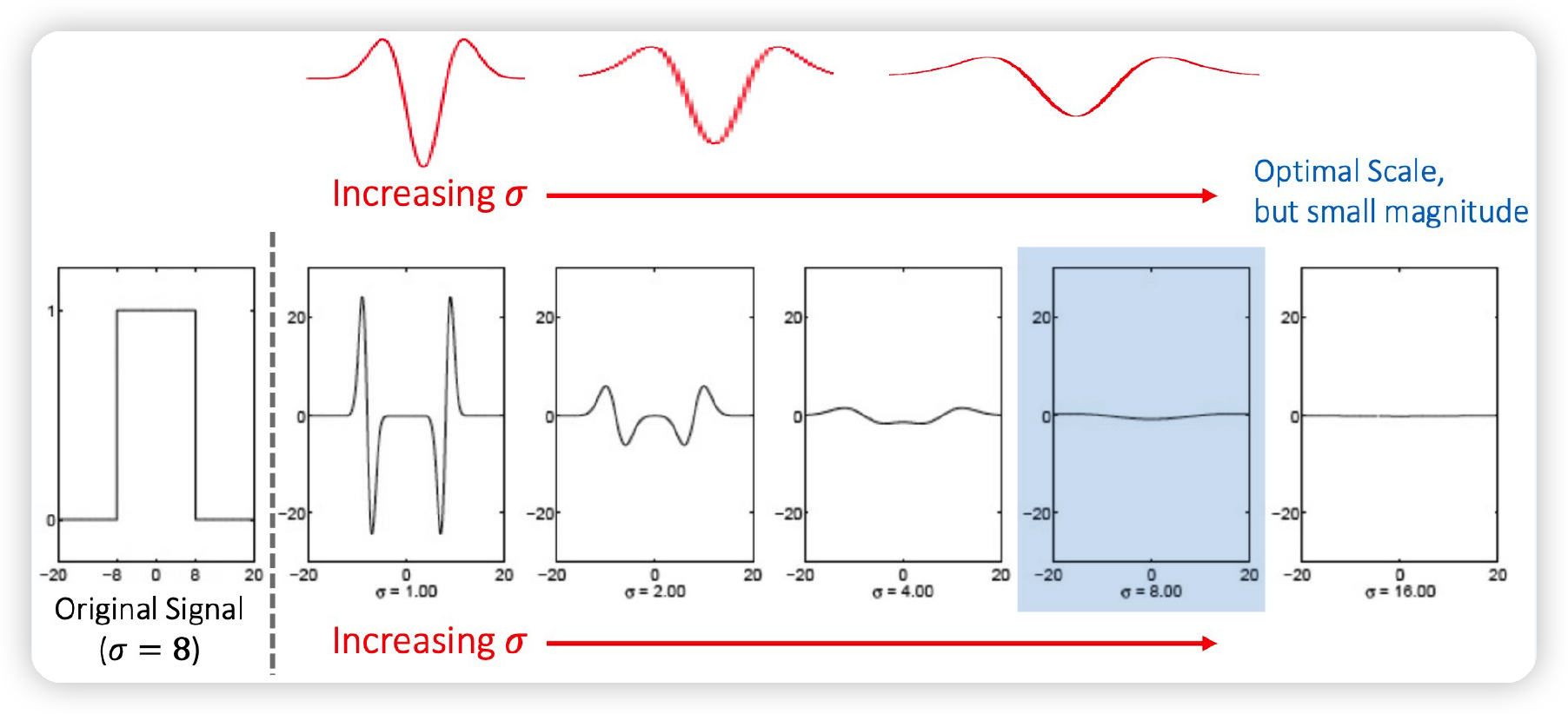
하지만, Laplacian값의 크기는 scale에 dependent한다. ( 아래 그림 참조 )
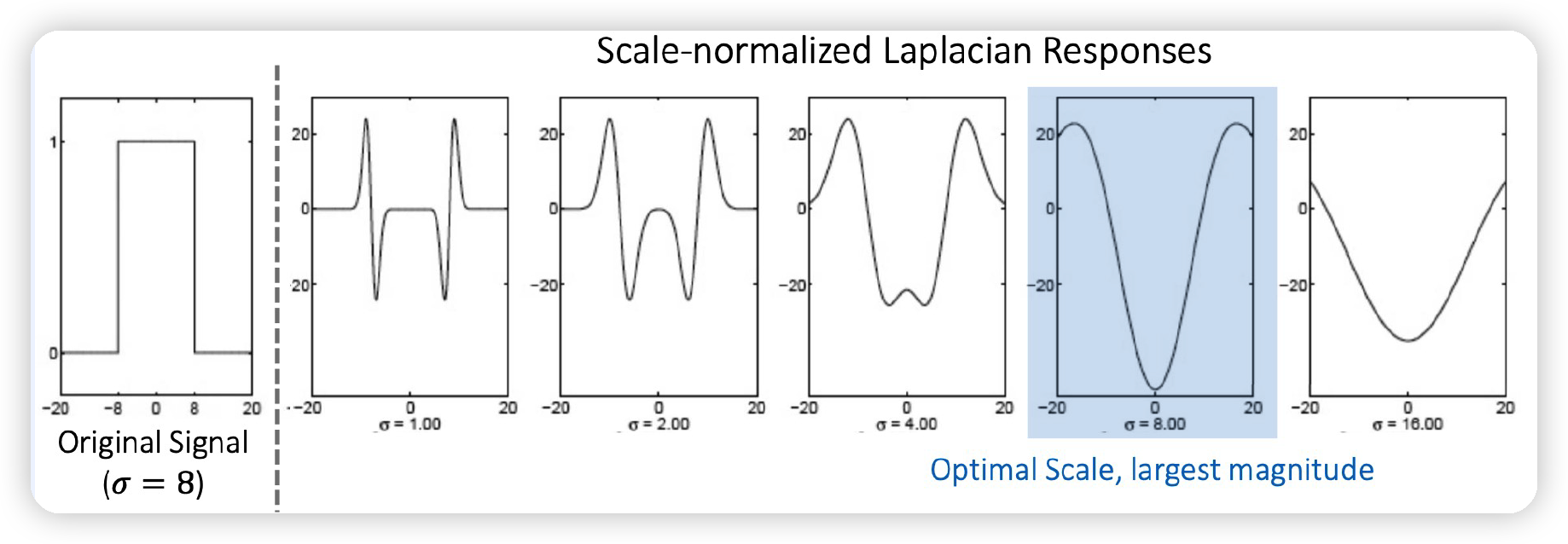
따라서, scale normalization을 수행해준다!
\(\rightarrow\) \(\nabla_{\text {norm }}^{2} G=\sigma^{2} \nabla^{2} G\)
6. SIFT ( Scale-Invariant Feature Transform )
가장 대표적인 local image descriptor
SIFT를 사용하여, 주변 점들 ( neighboring points )과 차이가 나는 점들을 찾는다!
SIFT 절차

( 각 절차에 대해서는, 아래에서 세부적으로 설명 )
(1) 절차 1 : Scale-Space Extrema 찾기
마찬가지로, LoG를 사용한다. ( 혹은 DoG도 가능 )
-
LoG : \(\begin{aligned} \nabla^{2} G(x, y, \sigma) &=\frac{\partial^{2} G}{\partial x^{2}}+\frac{\partial^{2} G}{\partial y^{2}} = \frac{x^{2}+y^{2}-2 \sigma^{2}}{\sigma^{4}} G(x, y, \sigma) \end{aligned}\)
- Intereseting point detection ( ex. keypoint, blobl )
- optimal scale \(\sigma\)를 찾는다
\(\rightarrow\) Scale normalized LoG : \(\nabla_{\text {norm }}^{2} G(x, y, \sigma)=\sigma^{2} \nabla^{2} G(x, y, \sigma)\).
DoG도 사용 가능!
-
DoG = 두 Gaussian의 차이
-
efficient approximation of LoG
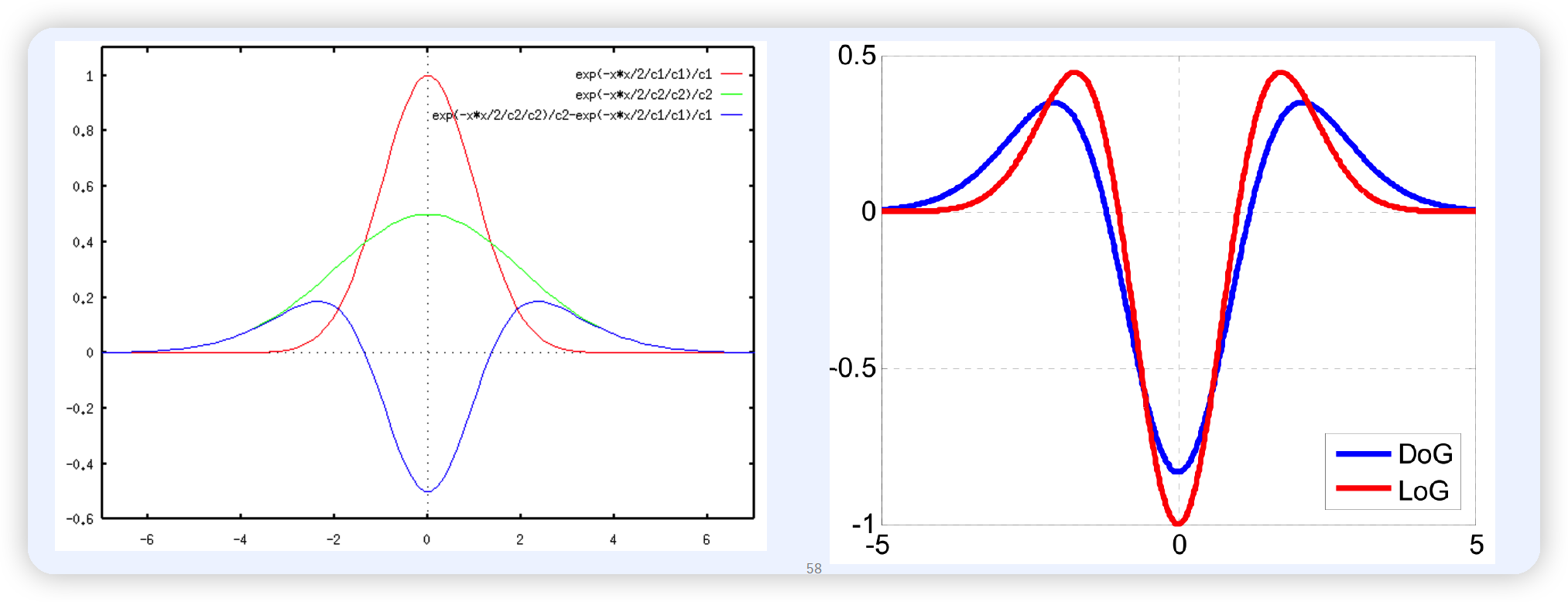
DoG = efficient approximation of LoG
\(\nabla^{2} G=\frac{\partial G}{\partial \sigma} \approx \frac{G(x, y, k \sigma)-G(x, y, \sigma)}{k \sigma-\sigma}\).
- \(\begin{aligned} G(x, y, k \sigma)-G(x, y, \sigma) & \approx(k-1) \sigma^{2} \nabla^{2} G \\ &=(k-1) \sigma^{2} \nabla_{\text {norm }}^{2} G \\ & \propto \nabla_{\text {norm }}^{2} G \end{aligned}\).
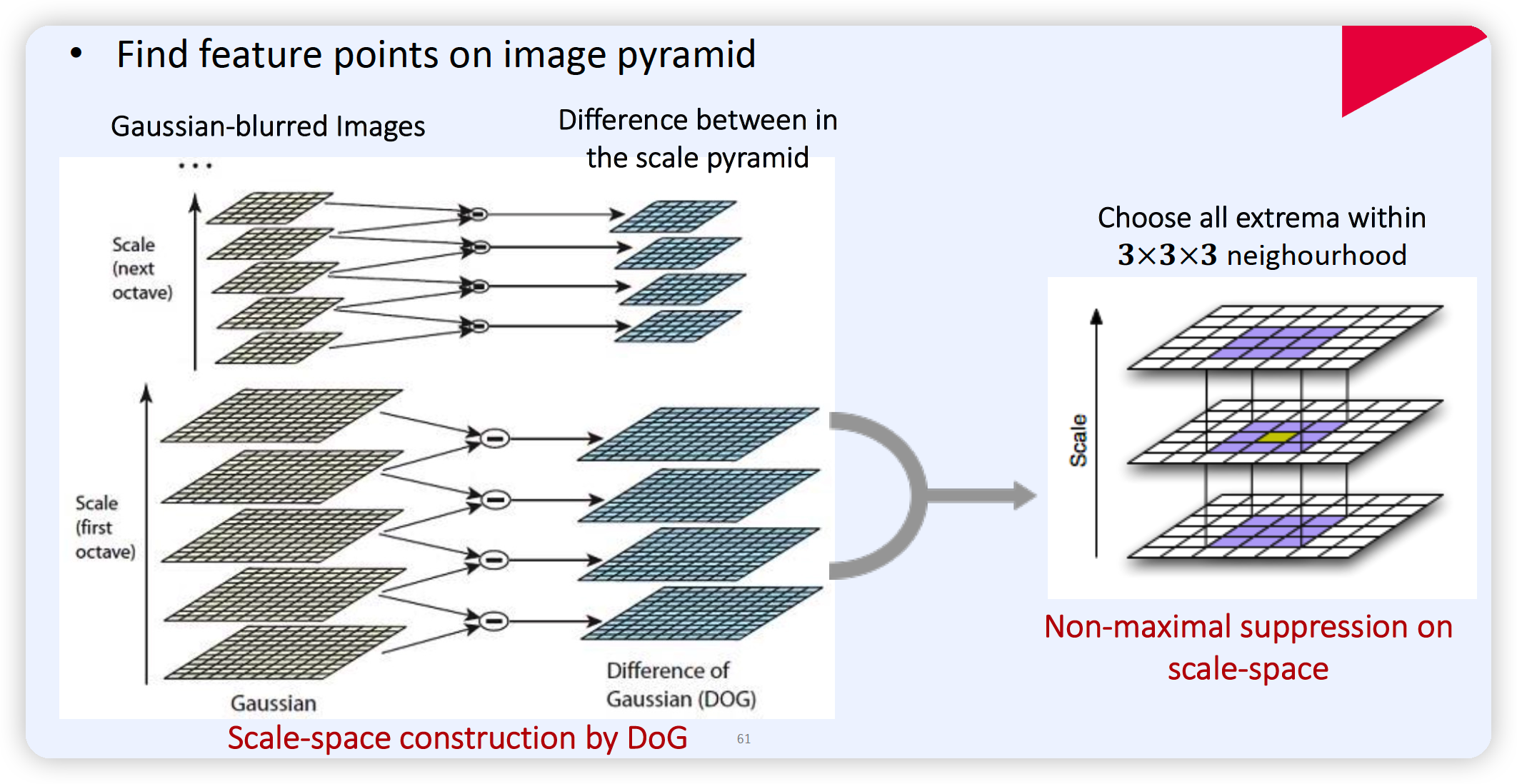
(2) KeyPoint Filtering
2-1) “대조가 낮은” keypoint를 제거한다.
( = DoG response가 일정 threshold를 넘지 못하면, 버린다 )
- \(\mid D (x)\mid < 0.03\).
2-2) “한 방향에서만 strong edge response가 나오는” keypoint를 제거한다.
-
알 수 있는 방법 : Hessian matrix
\(H=\left[\begin{array}{ll} D_{x x} & D_{x y} \\ D_{x y} & D_{y y} \end{array}\right] \quad \begin{aligned} &\operatorname{trace}(H)=D_{x x}+D_{y y}=\lambda_{1}+\lambda_{2} \\ &\operatorname{det}(H)=D_{x x} D_{y y}-\left(D_{x y}\right)^{2}=\lambda_{1} \lambda_{2} \end{aligned}\).
- \(\lambda_{1}, \lambda_{2}\) : two eigenvalues of \(H\).
-
한 방향의 edge response :
- \(\frac{\operatorname{trace}(H)^{2}}{\operatorname{det}(H)}=\frac{\left(\lambda_{1}+\lambda_{2}\right)^{2}}{\lambda_{1} \lambda_{2}}=\frac{\left(\gamma \lambda_{2}+\lambda_{2}\right)^{2}}{\gamma \lambda_{2}^{2}}=\frac{(\gamma+1)^{2}}{\gamma}\).
\(\rightarrow\) \(\frac{\operatorname{trace}(H)^{2}}{\operatorname{det}(H)}>\delta\) 이면, 해당 keypoint 제거하기!
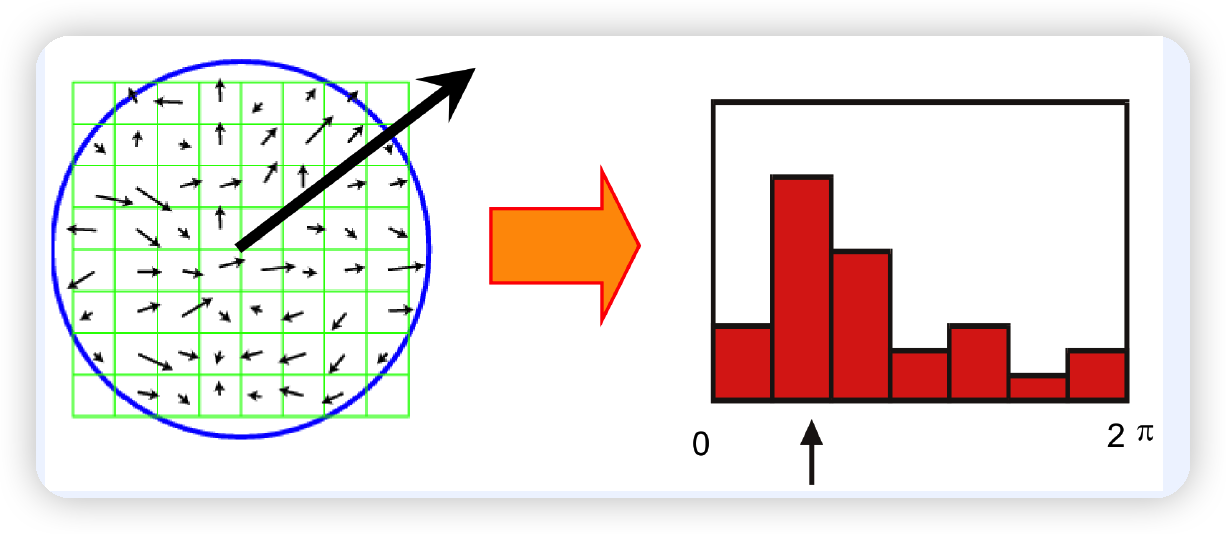
(3) Orientation Assignment
위 단계에서 keypoint를 찾았다.
이제, 해당 keypoint에서의 “orientation (\(\theta\) )”과, gradient의 “magnitude (\(m\))”를 계산한다.
\(\begin{aligned} &m(x, y)=\sqrt{\{L(x+1, y)-L(x-1, y)\}^{2}+\{L(x, y+1)-L(x, y-1)\}^{2}} \\ &\theta(x, y)=\tan ^{-1}\left[\frac{L(x, y+1)-L(x, y-1)}{L(x+1, y)-L(x-1, y)}\right] \end{aligned}\).
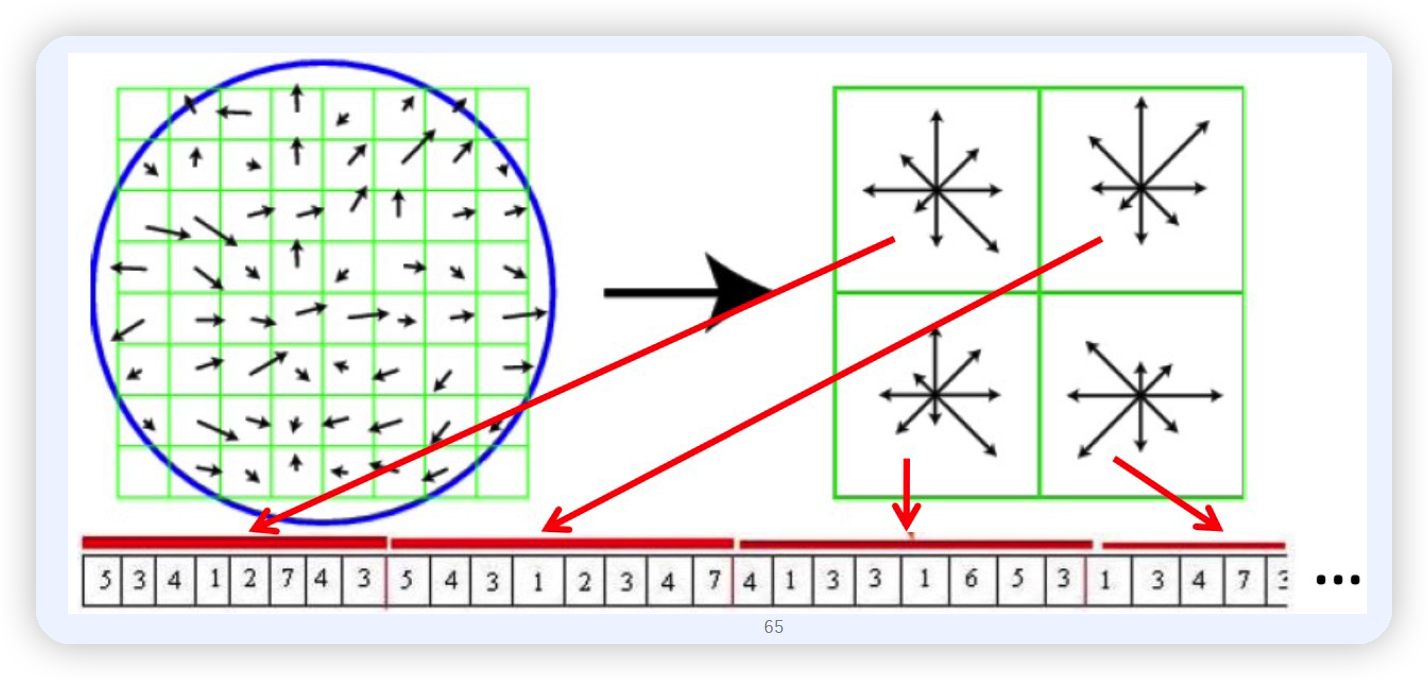
(4) Descriptor 계산하기
아래 그림과 같이 8x8=64 픽셀의 이미지가 있을 때,
이를 4개의 4x4=16 이미지로 partitioning한다.
그런 뒤, 각 partition별로, most dominant orientation 순으로 histogram값을 나열한다.
\(\rightarrow\) 4개의 이미지 x 8개의 방향(histogram의 bin 개수) = 32차원의 벡터
- L2-norm=1 normalization ( unit length 로 만들어주기 )
- PCA는 optional

