Automatic Shortcut Removal for-Self-Supervised Representation Learning
Contents
- Abstract
- Related Work
- Methods
- What are shortcuts
- Automatic Adversarial shortcut removal
0. Abstract
self-supervised learning : via pretext task
central challenge : feature ctraxtor quicly learns to exploit low-level features
\(\rightarrow\) fails to learn useful semantic representations
Solution : find such shortcut features
This paper : propose a general framework for mitigating the effect of shortcuts
1. Introduction
propose a simple method to remove shortcuts automatically
\(\rightarrow\) process images with a lightweight image-to-image translation network ( = lens )
-
once trained, lens can be applied to unseen images
& used in downstream tasks
2. Methods
process images with a lightweight image-to-image translation network ( = lens )
- trained adversarially, to REDUCE the performance on pretext tasks
(1) What are shortcuts
shortcuts
= lead to trivial solutions
= easily learnable features, that are predictive of the pretext label
Solution?
-
should encourage the network to learn non-shorcuts & shortcuts
-
solve this by…
-
providing both lensed & non-lensed images
& combining representations w & w/o shortcut removal
-
(2) Automatic Adversarial shortcut removal
Pretext task-based SSL
- loss function : \(\mathcal{L}_{\mathrm{SSL}}=\sum_{i=1}^N L_{\mathrm{SSL}}\left(F\left(x_i\right), y_i\right)\)
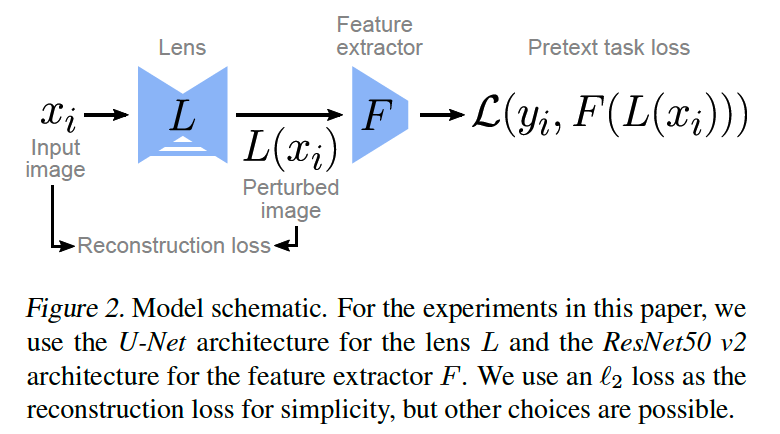
Introduce lens network \(L\) to remove shortcuts
- (slightly) modifies its inputs \(x_i\) & maps them back to the input space
( before feeding them to the representation network \(F\) )
-
train the lens adversarially against \(\mathcal{L}_{\mathrm{SSL}}\) to increase the difficulty of the pretext-task
-
loss function : \(\mathcal{L}_{\mathrm{SSL}}=\sum_{i=1}^N L_{\mathrm{SSL}}\left(F\left(L\left(x_i\right)\right), y_i\right)\)
-
2 loss variants
[ Full adversarial loss ]
- negative task loss : \(\mathcal{L}_{\text {adv }}=-\mathcal{L}_{\text {SSL}}\).
[ Least likely adversarial loss ]
- \(\mathcal{L}_{\text {adv }} =\sum_{i=1}^N L_{\mathrm{SSL}}\left(F\left(L\left(x_i\right)\right), y_i^{\mathrm{LL}}\right)\),
- where \(y_i^{\mathrm{LL}} =\underset{y}{\arg \min } p\left(y \mid F\left(L\left(x_i\right)\right)\right)\)
lens is also trained with a reconstruction loss to avoid trivial solutions
- \(\mathcal{L}_{\text {lens }}=\mathcal{L}_{\text {adv }}+\lambda \mathcal{L}_{\text {rec }}\)/
- where \(\mathcal{L}_{\text {rec }}=\sum_{i=1}^N \mid \mid x_i-L\left(x_i\right) \mid \mid _2^2\)


