(paper 46) Barlow Twins

Barlow Twins : Self-Supervised Learning via Redundancy Reduction

Contents

1. Abstract
2. Method
   1. Description of Barlow Twins
   2. Implementation Details

0. Abstract

Issue in SSL : existence of trivial constant solutions

Solution : propose a new objective function

Barlow Twins

• Proposed objective function :
  • avoids collapse by measuring the cross-correlation matrix between the outputs of two identical networks fed with distorted versions of a sample
• does not require large batches
• does not require other etc …
  • asymmetry between the network twins such as a predictor network, gradient stopping, or a moving average on the weight updates

1. Method

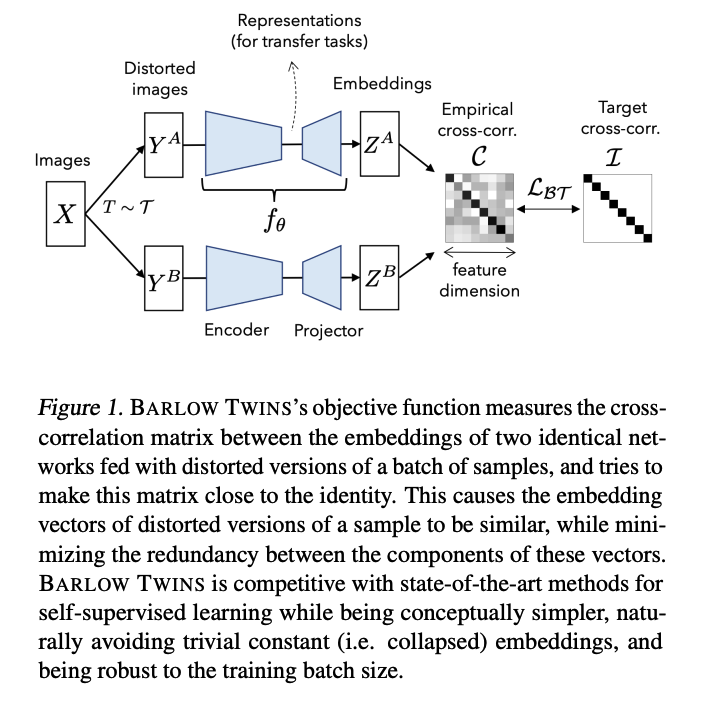
(1) Description of Barlow Twins

produces two distorted views ( via data augmentations \(\mathcal{T}\) )

• distorted views \(Y^A\) and \(Y^B\)

Feed two views to \(f_\theta\)

• produces embeddings \(Z^A\) and \(Z^B\)

  ( mean centered along the batch dimension )

Innovative loss function \(\mathcal{L}_{\mathcal{B} \mathcal{T}}\) :

\(\mathcal{L}_{\mathcal{B} \mathcal{T}} \triangleq \underbrace{\sum_i\left(1-\mathcal{C}_{i i}\right)^2}_{\text {invariance term }}+\lambda \underbrace{\sum_i \sum_{j \neq i} \mathcal{C}_{i j}^2}_{\text {redundancy reduction term }}\).

• \(\mathcal{C}\) :cross-correlation matrix,
  • between the outputs of the two identical networks along the batch dimension
  • \(\mathcal{C}_{i j} \triangleq \frac{\sum_b z_{b, i}^A z_{b, j}^B}{\sqrt{\sum_b\left(z_{b, i}^A\right)^2} \sqrt{\sum_b\left(z_{b, j}^B\right)^2}}\).
• (loss term 1) invariance term
  • encourage diagonal term to be 1
• (loss term 2) redundancy reduction term
  • encourage the off-diagonal term to be close to zero

(2) Implementation Details