TabNet: Attentive Interpretable Tabular Learning

0. Abstract

TabNet

novel high-performance & interpretable canonical deep tabular data learning architecture
uses sequential attention to choose which features to reason

\(\rightarrow\) enable interpretability
efficient learning

Main contributions

inputs raw tabular data ( without any preprocessing ) & end-to-end DL
uses sequential attention to choose which features to reason from
- enable interpretation
- feature selection is instance-wise
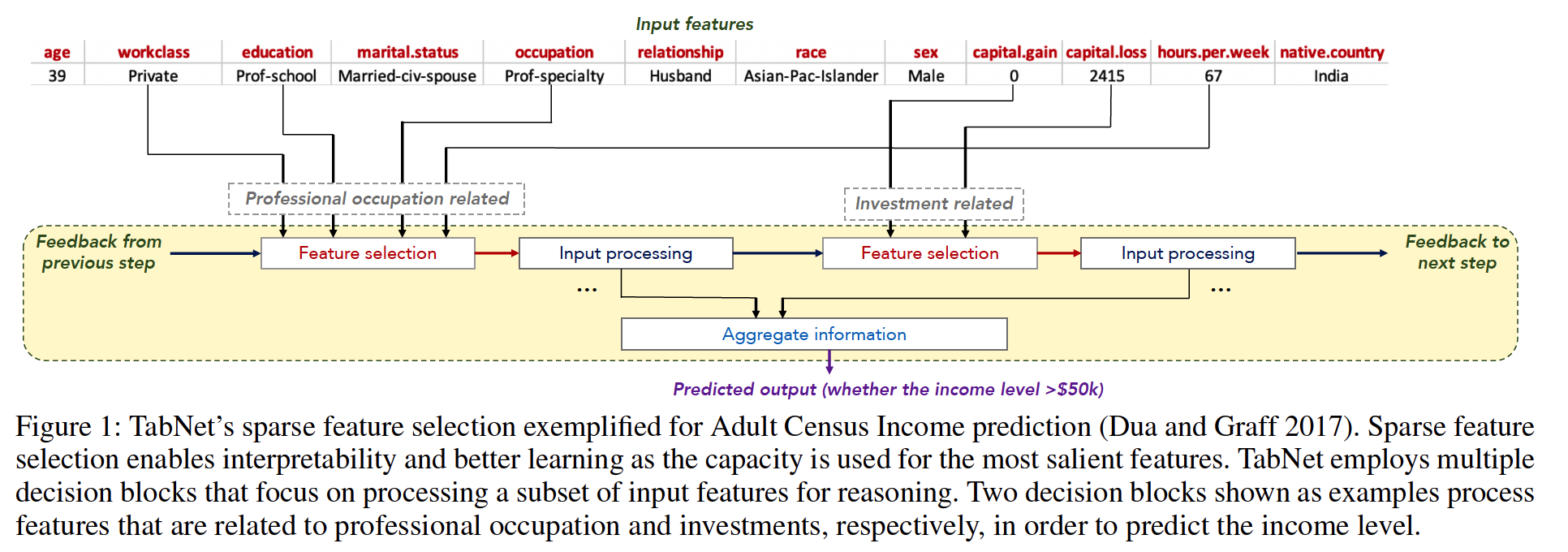
2 valuable properties :
- (1) outperforms other models ( both in cls & reg )
- (2) enables two kinds of interpretability :
  - local interpretability : visualizes the importance of features & how they are combined
  - global interpretability : quantifies the contribution of each feature to the trained model.
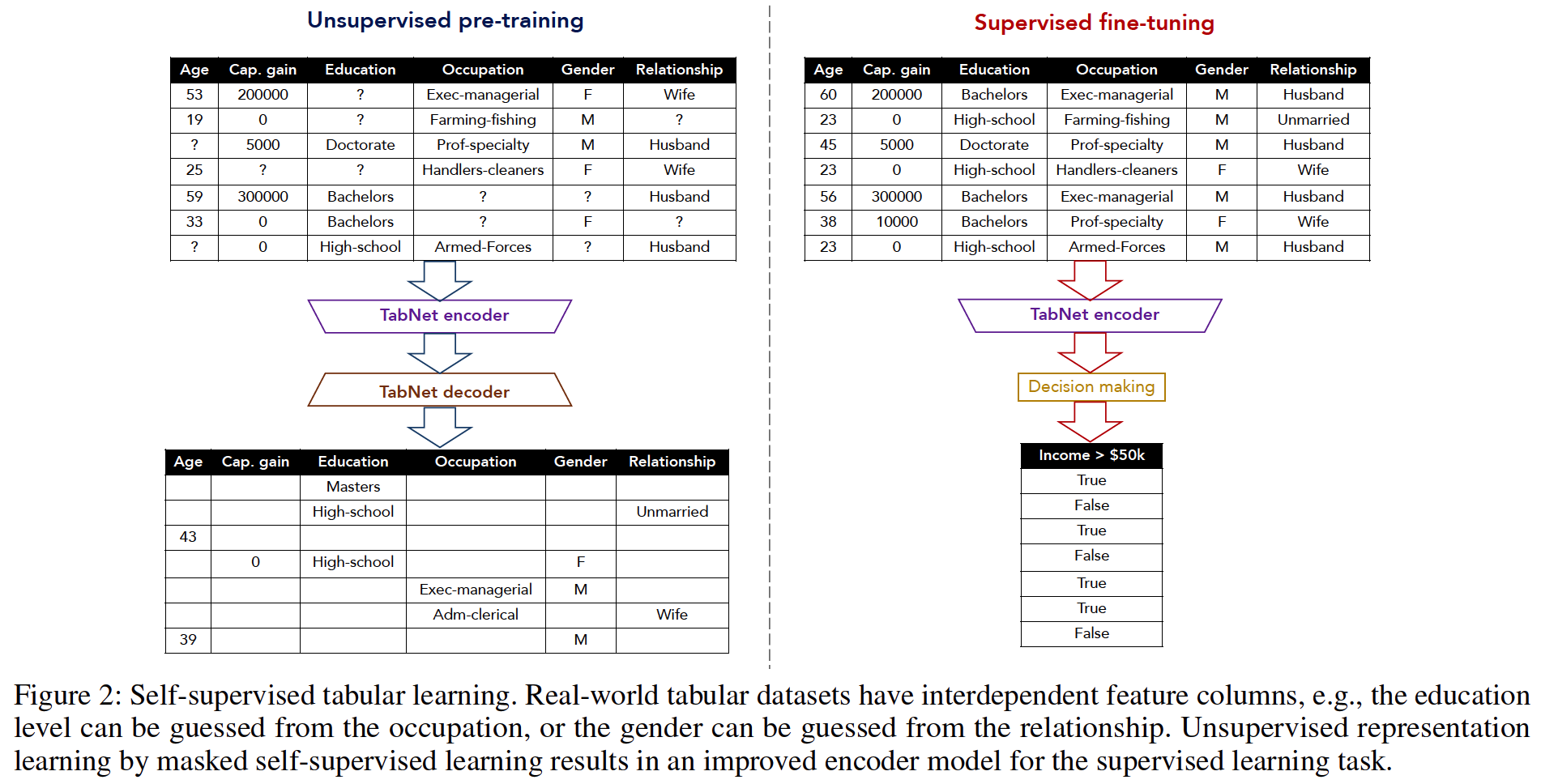
show significant performance improvements,

by using unsupervised pre-training to predict masked features

conventional DNN building blocks can be used to implement DT-like output manifold

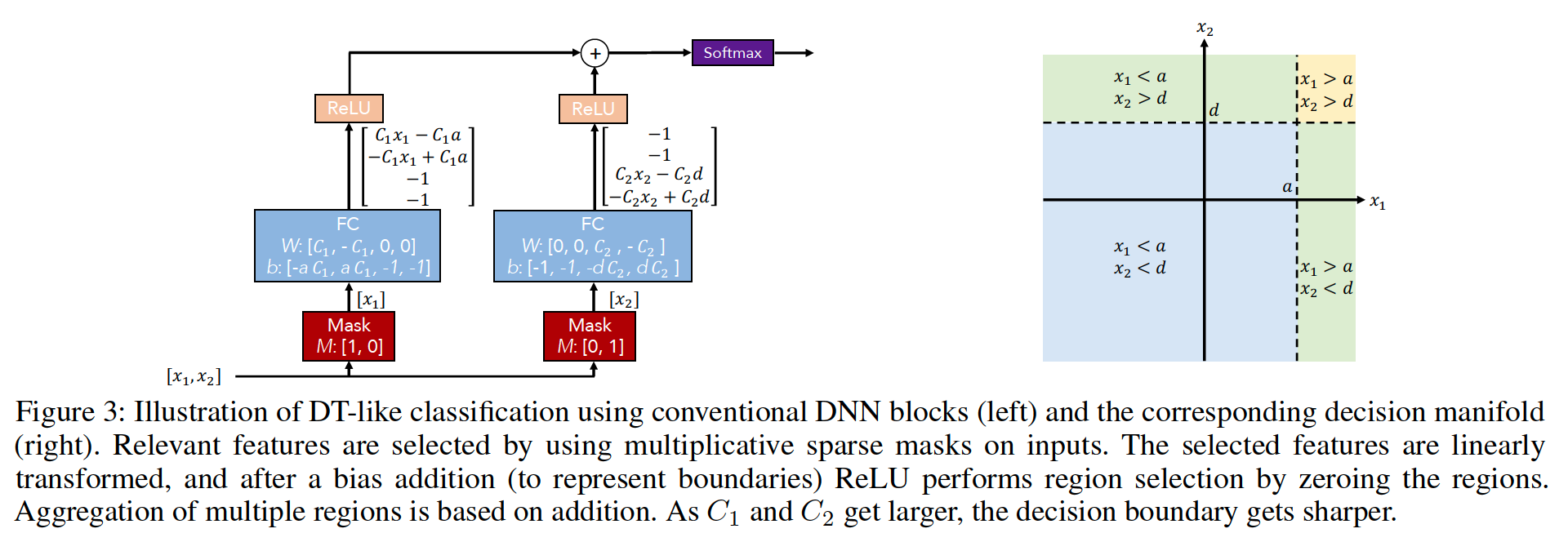
TabNet : outperforms DTs

(i) uses sparse instance-wise feature selection learned from data
(ii) constructs a sequential multi-step architecture
- each step contributes to a portion of the decision based on the selected features
(iii) improves the learning capacity via nonlinear processing of the selected features
(iv) mimics ensembling via higher dimensions and more steps.

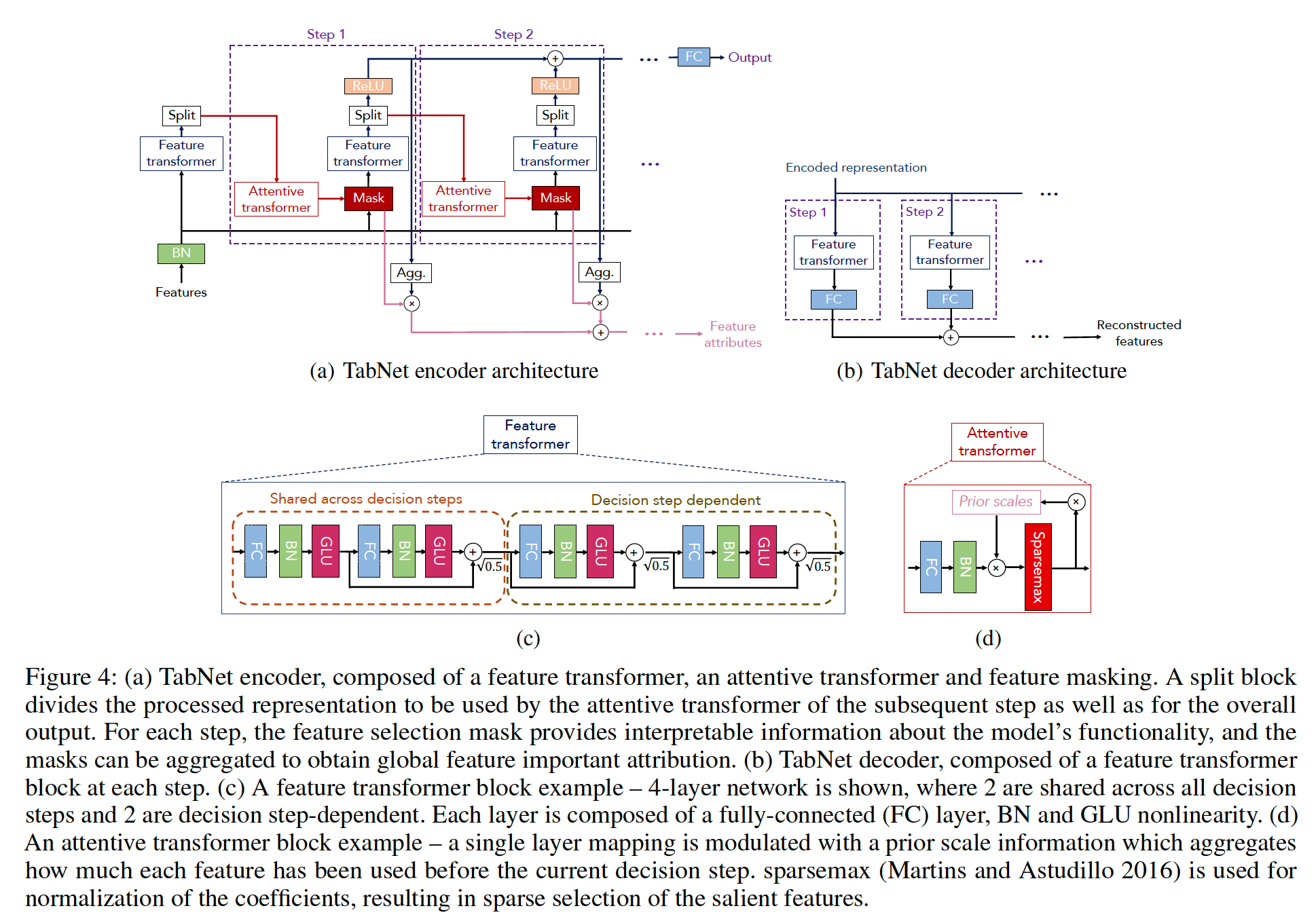
Details :

[input] numeric & categorical
- raw numerical features
- mapping of categorical features ( with trainable embeddings )
pass the \(D\) dim features \(\mathbf{f} \in \Re^{B \times D}\) to each decision step
encoding : based on sequential multi-step processing with \(N_{\text {steps }}\) decision steps
\(i^{t h}\) step :
- input : processed information from the \((i-1)^{t h}\) step
- process : decide which features to use
- output : processed feature representation
  
  ( to be aggregated into the overall decision )

learnable mask \(\mathbf{M}[\mathbf{i}] \in\) \(\Re^{B \times D}\) ( for soft selection of the salient features )

multiplicative mask : \(\mathbf{M}[\mathbf{i}] \cdot \mathbf{f}\)
use attentive transformer to obatin the masks
\(\mathbf{M}[\mathbf{i}]=\operatorname{sparsemax}\left(\mathbf{P}[\mathbf{i}-\mathbf{1}] \cdot \mathrm{h}_i(\mathbf{a}[\mathbf{i}-\mathbf{1}])\right)\).
- Sparsemax normalization : encourages sparsity by mapping the Euclidean projection onto the probabilistic simplex
- \(\sum_{j=1}^D \mathbf{M}[\mathbf{i}]_{\mathbf{b}, \mathbf{j}}=1\).
- \(\mathrm{h}_i\) is a trainable function ( using FC layer )
- \(\mathbf{P}[\mathbf{i}]=\prod_{j=1}^i(\gamma-\mathbf{M}[\mathbf{j}])\), where \(\gamma\) is relaxation parameter
  - \(\mathbf{P}[\mathbf{0}]\) : initialized as 1
sparse selection of the most salient features

\(\rightarrow\) model becomes more parameter efficient.
for further sparisty … sparsity regularization
- \(L_{\text {sparse }}=\sum_{i=1}^{N_{\text {steps }}} \sum_{b=1}^B \sum_{j=1}^D \frac{-\mathbf{M}_{\mathbf{b}, \mathbf{j}}[\mathbf{i}] \log \left(\mathbf{M}_{\mathrm{b}, \mathrm{j}}[\mathbf{i} \mathbf{i}]+\mathrm{c}\right)}{N_{\text {steps }} \cdot B}\).
- add the sparsity regularization to the overall loss ( with a coefficient \(\lambda_{\text {sparse }}\))

process the filtered features using a feature transformer

\([\mathbf{d}[\mathbf{i}], \mathbf{a}[\mathbf{i}]]=\mathrm{f}_i(\mathbf{M}[\mathbf{i}] \cdot \mathbf{f})\) : split for…

pass