TS2Vec: Towards Universal Representation of Time Series
Contents
- Abstract
- Introduction
- Method
- Problem Definition
- Model Architecture
- Contextual Consistency
- Hierarchical Contrasting
0. Abstract
TS2Vec
-
universal framework for learning representations for TS in an arbitrary semantic level
-
perform contrastive learning in anhierarchical way
-
representation of sub-sequence of TS
= simple aggregation over time steps
1. Introduction
Recent works in learning representations of TS using contrastive loss
\(\rightarrow\) has 3 limitations
Limitations
-
instance-level representations may not be suitable for tasks that need fine-grained representations
-
ex) anomaly detection, TS forecasting
\(\rightarrow\) insufficient with coarse-grained representations
-
-
few existing methods consider the multi-scale contextual information
- Multi-scale features : may provide different level of semantics & improve generalizaiton
-
most are inspired by CV, NLP
\(\rightarrow\) strong inductive bias ( ex. transformation-invariance, cropping-invariance)
propose TS2Vec to overcome these issues
-
representation learning of TS in all semantic levels
-
hierarchically discriminates positive & negative samples,
at instance-wise & temporal dimensions
-
also obtain representation for an arbitrary sub-series
( by using max-pooling )
2. Method
(1) Problem Definition
- \(N\) time series : \(\mathcal{X}=\left\{x_1, x_2, \cdots, x_N\right\}\)
- encoder : \(f_{\theta}\)
- representation : \(r_i=\left\{r_{i, 1}, r_{i, 2}, \cdots, r_{i, T}\right\}\)
- where \(r_{i, t} \in \mathbb{R}^K\) & \(K\) : dimension of representation vectors
(2) Model Architecture
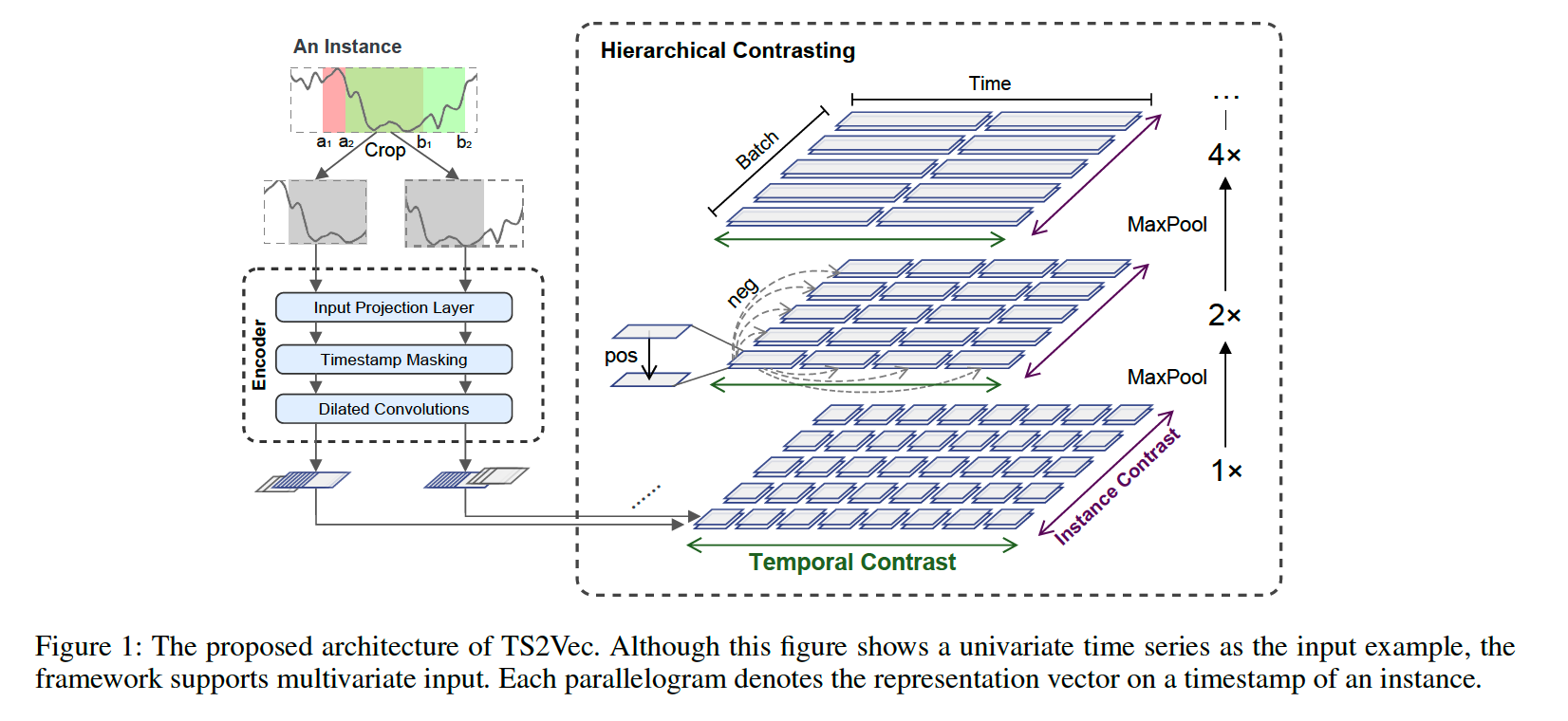
Procedure
-
(1) randomly sample 2 overlapping subseries from \(x_i\)
-
(2) feed inputs to encoder
-
(3) jointly optimized with temporal contrastive loss & instance-wise contrastive loss
Encoder \(f_{\theta}\) : 3 components
Components
- (1) input projection layer
- (2) timestamp masking module
- (3) dilated CNN
a) input projection layer
- FC layer
- maps \(x_{i,t}\) into \(z_{i,t}\)
b) timestamp masking module
- masks latent vectors at randomly selected timestamps
-
generate an augmented context view
-
why not on raw value, but latent value?
\(\rightarrow\) the value range for raw TS is possibliy unbounded & impossible to find a special token for raw TS
c) dilated CNN
- with 10 residual blocks
- each block : two 1D conv layers, with dilation parameter \(2^l\)
(3) Contextual Consistency
How to consruct positive pairs?
(Previous works)
- subseries consistency
- positive, if closer to its sampled subseries
- temporal consistency
- by choosing adjacenc segments as positive samples
- transformation consistency
- encourage model to learn transformation invariant representations
Limitations :
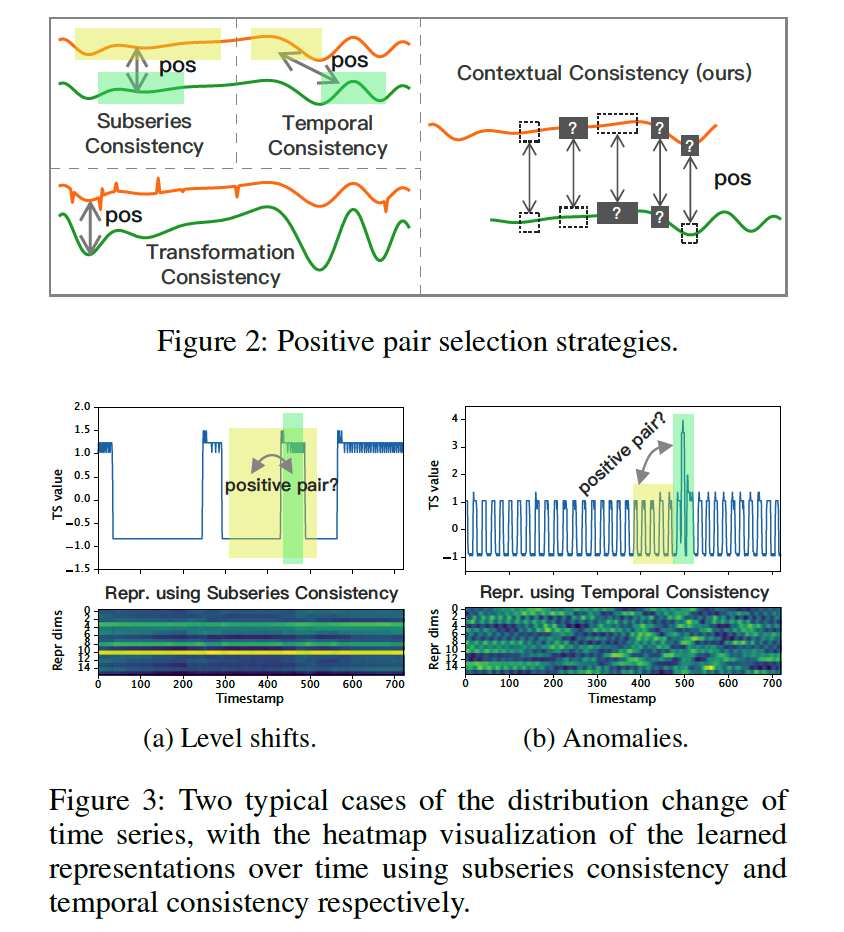
Fig 3-a & 3-b)
- green & yello have differen patterns, but previous works considers them as positive
\(\rightarrow\) propose contextual consistency
Contextual Consistency
-
Considers representations at same timestamp in 2 augmented contexts as positive
-
how to generate context? by applying..
- (1) timestamp masking
- (2) random cropping
-
benefits of (1) & (2)
-
benefit 1) do not change magnitude of TS
-
benefit 2) improve the robustness of representations,
by forcing each timestamp to reconstruct itself in *distinct contexts8
-
a) Timestamp Masking
- to produce new context view
- masks the latent vector \(z_i=\left\{z_{i, t}\right\}\)
- mask with binary mask \(m \in\{0,1\}^T\)
- Bernoulli distn with \(p=0.5\)
b) Random Cropping
for any TS input \(x_i \in \mathbb{R}^{T \times F}\),
-
randomly sample 2 overlapping segments \(\left[a_1, b_1\right],\left[a_2, b_2\right]\)
- \(0<a_1 \leq a_2 \leq b_1 \leq\) \(b_2 \leq T\)
-
overlapped segment : \(\left[a_2, b_1\right]\)
\(\rightarrow\) should be consistent for 2 context reviews
(4) Hierarchical Contrasting
propose Hierarchical Contrastive loss
- force the cndoer to learn representations at various scales

To capture contextual representations of TS,
leverage both (1) instance-wise & (2) temporal contrastive loss
a) temporal contrastive loss
- same timestamp from 2 views = positive
- different time stamp ~ = negative
\(\left.\ell_{t e m p}^{(i, t)}=-\log \frac{\exp \left(r_{i, t} \cdot r_{i, t}^{\prime}\right)}{\sum_{t^{\prime} \in \Omega}\left(\exp \left(r_{i, t} \cdot r_{i, t^{\prime}}^{\prime}\right)+\mathbb{1}_{\left[t \neq t^{\prime}\right]} \exp \left(r_{i, t} \cdot r_{i, t^{\prime}}\right)\right.}\right)\).
- \(\Omega\): set of timestamps within the overlap of the two subseries
b) instance-wise contrastive loss
- representations of other TS at timestamp \(t\) in the same batch : negative samples
\(\ell_{i n s t}^{(i, t)}=-\log \frac{\exp \left(r_{i, t} \cdot r_{i, t}^{\prime}\right)}{\sum_{j=1}^B\left(\exp \left(r_{i, t} \cdot r_{j, t}^{\prime}\right)+\mathbb{1}_{[i \neq j]} \exp \left(r_{i, t} \cdot r_{j, t}\right)\right)},\).
- \(B\) : batch size
c) Overall Loss
\(\mathcal{L}_{\text {dual }}=\frac{1}{N T} \sum_i \sum_t\left(\ell_{\text {temp }}^{(i, t)}+\ell_{i n s t}^{(i, t)}\right)\).
