(1) Introduction

1. Introduction

1-1. Optimization Problems

최적 해 (Optimal Value) 찾는 문제

• ex) ML의 loss function을 minimze하는 파라미터 구하기

Mathematical optimization problems

(1) 문제 정리

\(\min _{x \in D} f(x)\).

• subject to \(g_{i}(x) \leq 0, i=1, \ldots m\)
• subject to \(h_{j}(x)=0, j=1, \ldots r\)

(2) 용어 정리

• \(x \in R^{n}\) : optimization variable
• \(f: R^{n} \rightarrow R\) : objective function
• \(g_{i}: R^{n} \rightarrow R, i=1, \ldots, m\) : inequality constraint functions

• \(h_{i}: R^{n} \rightarrow R, j=1, \ldots, r\) : equality constraint functions

• \(x^{*}\) : optimal value(solution)

(3) 제약조건

2종류의 제약조건이 있다.

• a) Explicit constraints

  • 명시적 제약조건
  • 이러한 제약이 없는 문제를 “unconstrained problem”이라고 함

• b) Implicit constraints

  • 직접적으로 명시되지 않은 제약 조건

  • objective function & 모든 constraint function들의 “정의역에 대한 교집합”

    ( 즉, \(D=\operatorname{dom}(f) \cap \bigcap_{i=1}^{m} \operatorname{dom}\left(g_{i}\right) \cap \bigcap_{j=1}^{r} \operatorname{dom}\left(h_{j}\right)\) )

example)

• 문제 : minimize \(log (x)\)
• implicit constraints : \(x>0\)

1-2. Convex Optimization Problem

1) 문제 정리

\(\min _{x \in D} f(x)\).

• subject to \(g_{i}(x) \leq 0, i=1, \ldots m\)
• subject to \(h_{j}(x)=0, j=1, \ldots r\)

+ 여기서, \(f\) & \(g_i\) 가 convex이고, \(h_j\)가 affine

( affine function )

• \(h_j(x) = a_j^{T}x + b_j\) , where \(j=1,…,r\)

Convex Sets

(1) 선분 (line segment)

• \(x=\theta{x_1} + (1-\theta)x_2\), where \(0 \leq \theta \leq 1\)

(2) convex set

• 어떤 집합(set)이 있고, 이 안에 있는 두 점 \(x_1\) & \(x_2\) 를 잇는 선분이, 이 집합안에 속할 때

  이 집합을 convex set이라고 한다

• \(x_{1}, x_{2} \in C, 0 \leq \theta \leq 1 \Rightarrow \theta x_{1}+(1-\theta) x_{2} \in C\).

(3) 그림

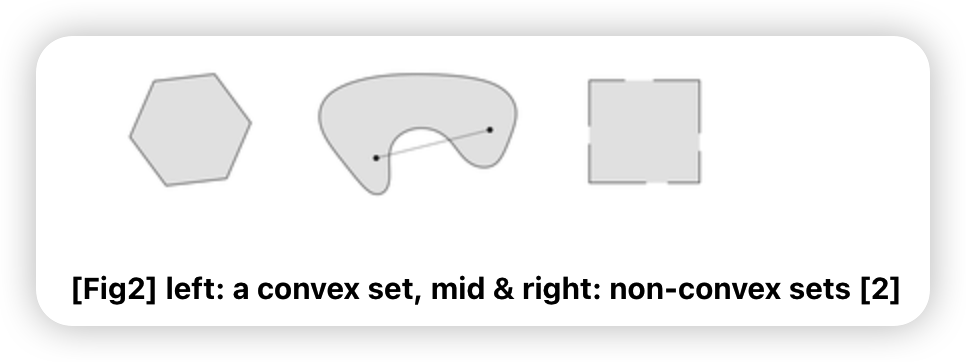
Convex Functions

(1) 정의

\(f: R^{n} \rightarrow R\) is convex if dom \(\mathrm{f}\) is a convex set and \(f(\theta x+(1-\theta) y) \leq \theta f(x)+(1-\theta) f(y)\) for all \(x, y \in\) dom \(\mathrm{f}, 0 \leq \theta \leq 1\)

(2) 그림

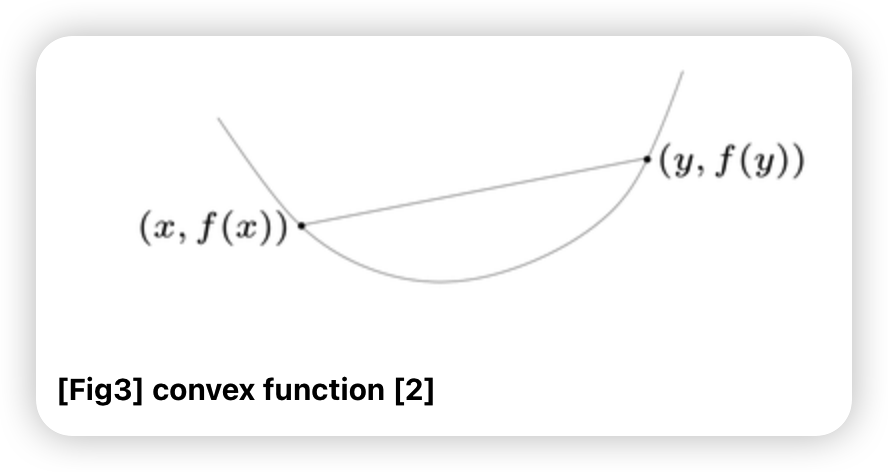
Convex set & Convex function의 관계

함수 \(f\)의 epigraph가 convex set이면, \(f\)는 convex function

• epigraph란?

  • epi = “above”
  • epigraph = “above the graph” = \(f\) 위 쪽의 영역

• epigraph의 수식적 정의

  • epigraph of f: \(R^{n} \rightarrow R\) :

    epi \(f=\left\{(x, t) \in R^{n+1} \mid x \in\right.\) dom \(\left.\mathrm{f}, \mathrm{f}(x) \leq t\right\}\)

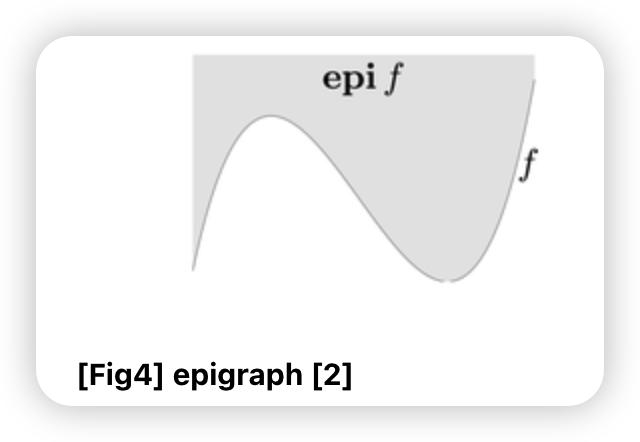
Convex Property of convex optimization problems

• non-convex인 경우 보다, 일반적으로 더 쉽게 풀 수 있음

• “Convex 함수의 local minimum은 항상 global minimum이다” 라는 특징 때문에

  ( 증명 생략 )

Convex Combination

• \(x=\theta_{1} x_{1}+\theta_{2} x_{2}+\ldots+\theta_{k} x_{k} \text { with } \theta_{1}+\ldots+\theta_{k}=1, \theta_{i} \geq 0\).

Affine Combination

• \(x=\theta_{1} x_{1}+\theta_{2} x_{2}+\ldots+\theta_{k} x_{k} \text { with } \theta_{1}+\ldots+\theta_{k}=1\).