(강의) Duality

Duality

Contents

1. Introduction
2. LP에서의 Duality
3. Lagrangian
   1. Lagrangian function
   2. Lagrangian Dual function
   3. Lagrangian Dual function의 2가지 특징
4. Dual Problem
   1. 요약
   2. Strong duality
   3. Strong duality 예시
5. Economic Interpretation

1. Introduction

Primal & Dual

• Primal : 원 문제
• Dual : 쌍대 문제

Dual Problem의 특징

• (1) concave function
• (2) Primal problem의 objective function의 lower bound
  • 만약, Dual problem의 최대값 = Primal problem의 최소값 \(\rightarrow\) STRONG duality

KKT condition

• 최적화를 푸는 가장 일반적인 방법

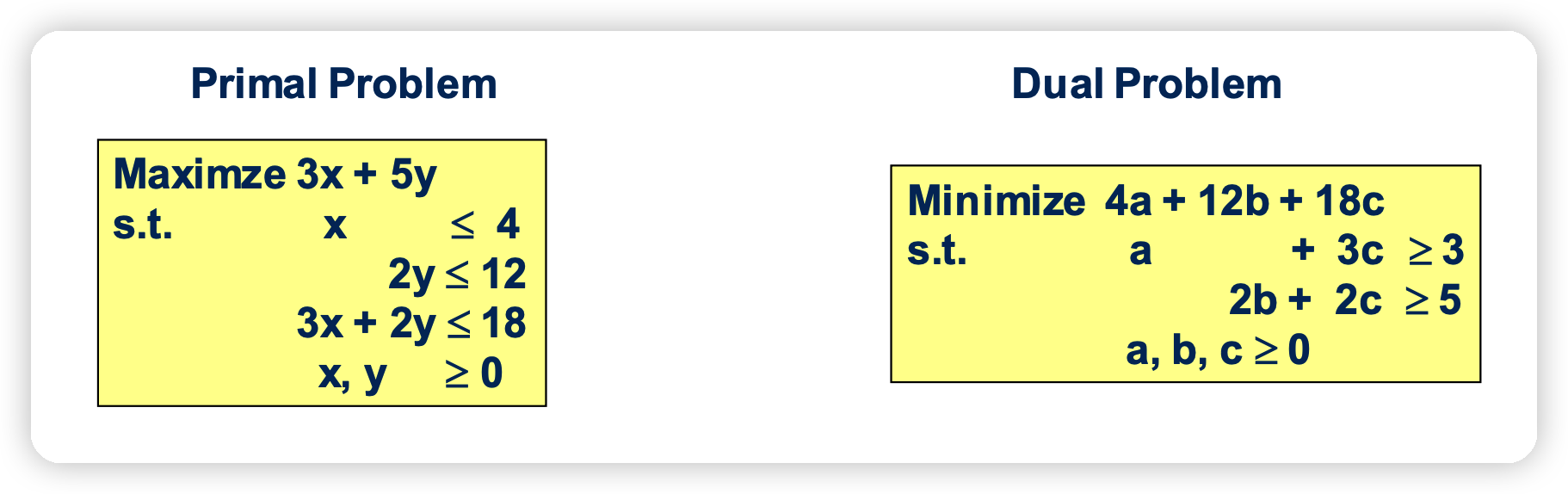
2. LP에서의 Duality

3. Lagrangian

minimize \(\quad f_{0}(x)\) subject to

• \[f_{i}(x) \leq 0, \quad i=1, \ldots, m\]
• \(h_{i}(x)=0, \quad i=1, \ldots, p\).

variable \(x \in \mathbf{R}^{n}\), domain \(\mathcal{D}\), optimal value \(p^{\star}\)

(1) Lagrangian function

• 목적 함수 & 제약식의 weighted sum 형태
• \(L(x, \lambda, \nu)=f_{0}(x)+\sum_{i=1}^{m} \lambda_{i} f_{i}(x)+\sum_{i=1}^{p} \nu_{i} h_{i}(x)\).
  • \(\lambda_{i}\) is Lagrange Multiplier associated with \(\mathrm{f}_{i}(\mathrm{x}) \leq 0\)
  • \(v_{i}\) is Lagrange Multiplier associated with \(\mathrm{h}_{i}(\mathrm{x})=0\)

example)

(1) Primal problem

• minimize \(f(x)=x_{1}^{2}+x_{2}^{2}\)
• subject to \(x_{1}+2 x_{2} \geq 2\)

(2) Standard form ( 제약식 : g(x) \(\leq\) k 꼴로 만들기! )

• minimize \(f(x)=x_{1}^{2}+x_{2}^{2}\)
• subject to \(-x_{1}-2 x_{2} \leq-2\)

(3) Lagrangian

• \(L(x, v)=x_{1}^{2}+x_{2}^{2}-v_{1}\left(x_{1}+2 x_{2}-2\right)\).

(2) Lagrangian Dual Function

\(g: \mathbf{R}^{m} \times \mathbf{R}^{p} \rightarrow \mathbf{R}\).

\(\begin{aligned} g(\lambda, \nu) &=\inf _{x \in \mathcal{D}} L(x, \lambda, \nu) \\ &=\inf _{x \in \mathcal{D}}\left(f_{0}(x)+\sum_{i=1}^{m} \lambda_{i} f_{i}(x)+\sum_{i=1}^{p} \nu_{i} h_{i}(x)\right) \end{aligned}\).

• 위 식에서 \(L\)은 Lagrangian function이다.

example)

(1) Lagrangian

• \(L(x, v)=x_{1}^{2}+x_{2}^{2}-v_{1}\left(x_{1}+2 x_{2}-2\right)\).

(2) Lagrangian Dual Function

• \(\begin{aligned} g(v)=\inf _{x} L(x, v) &=\inf _{\mathrm{x}}\left[x_{1}^{2}+x_{2}^{2}-v_{1}\left(x_{1}+2 x_{2}-2\right)\right] \\ &=\inf _{x}\left[\left(x_{1}^{2}-v_{1} x_{1}\right)+\left(x_{2}^{2}-2 v_{1} x_{2}\right)+2 v_{1}\right] \end{aligned}\).
  • 이를 infimum을 달성하는 \(x_1\) 와 \(x_2\)를 ( v에 관한 식으로 ) 정리해서 대입하면…
• \(g(v) = -\frac{5}{4}v_1^2 + 2v_1\).

(3) Lagrangian Dual Function의 2가지 특징

1) concave function

\(g(\lambda, \nu) =\inf _{x \in \mathcal{D}}\left(f_{0}(x)+\sum_{i=1}^{m} \lambda_{i} f_{i}(x)+\sum_{i=1}^{p} \nu_{i} h_{i}(x)\right)\).

• (1) Lagrangian은 \(x\)에 관한 AFFINE function 이다
• (2) AFFINE function은 concave하다
• (3) 2개의 concave 함수의 minimum 또한 concave하다

\(\rightarrow\) \(\therefore\) \(g(\lambda, \nu)\)는 concave function이다.

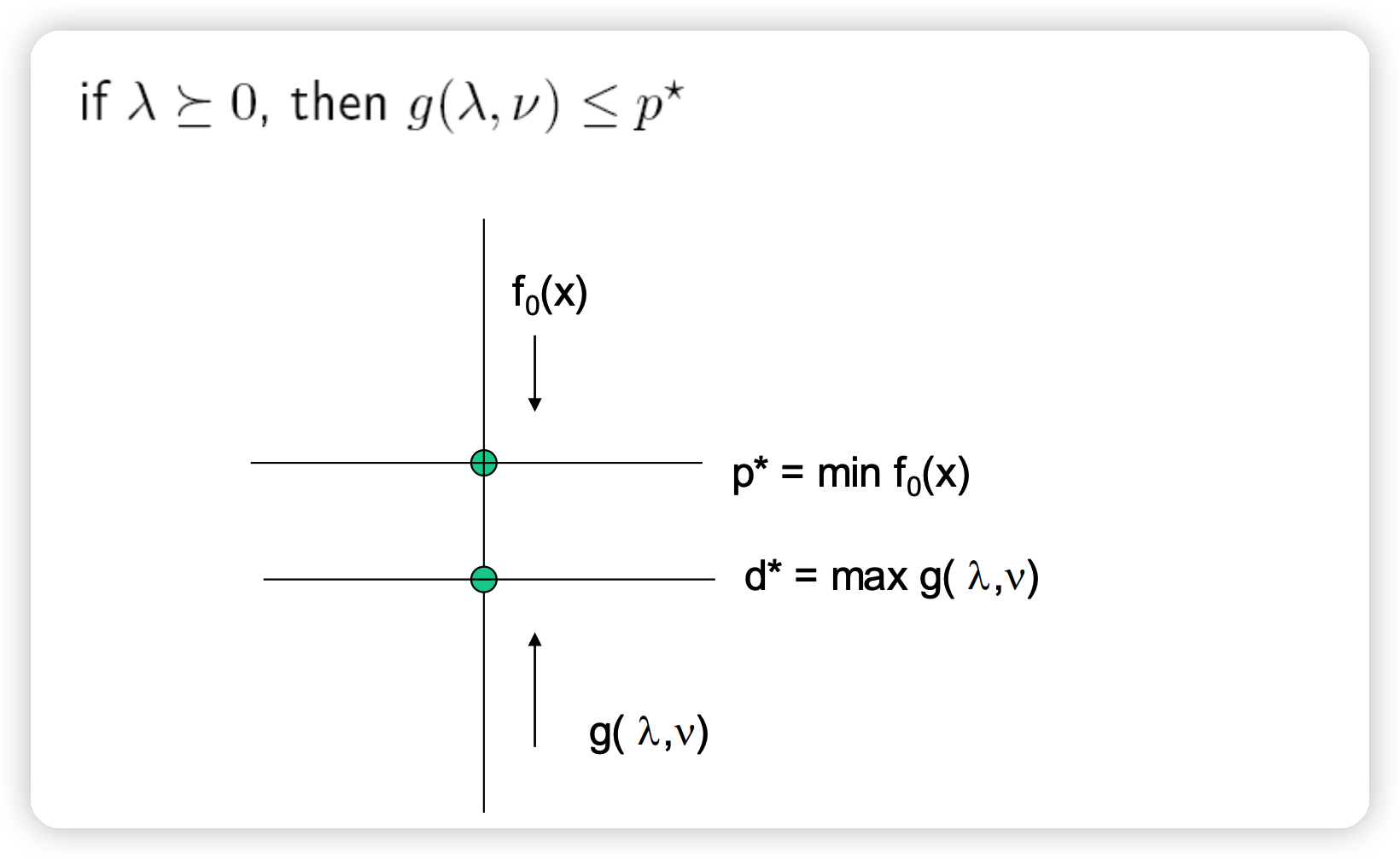
2) lower bound to original problem

4. Dual Problem

(1) 요약

Dual Problem : 항상 convex problem이다

• Primal Problem의 convex 여부와 무관

Weak duality ( \(p^{*} \geq d^{*}\) ) 는 항상 충족된다

Dual Problem을 품으로써, Primal Problem에 대한 좋은 lower bound를 얻을 수 있다.

(2) Strong duality : \(p^{*} = d^{*}\)

( 일반적으로, 잘 성립하지 않는다. Convex problem의 경우에 주로 성립한다 )

(1) Convexity

(2) Constraint Qualification

\(\rightarrow\) (1) & (2) implies STRONG duality

Slater’s Constraint Qualification

• there exists strictly feasible primal variables \(f_i(x)<0\).

(3) Strong duality 예시

아래의 문제가 Strong duality를 충족하는지 확인해보자.

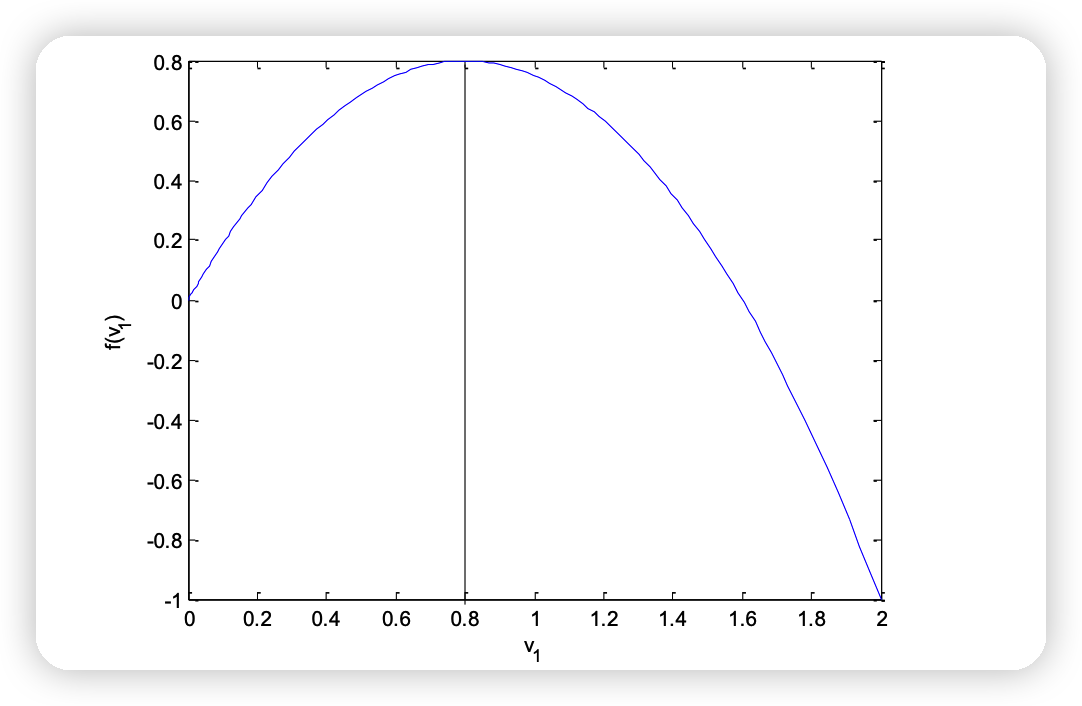
Dual Problem

\(v_1\) 이 0.8일때, 최대값을 달성한다

( \(g(v^{*}) = g(0.8) = 0.8\) )

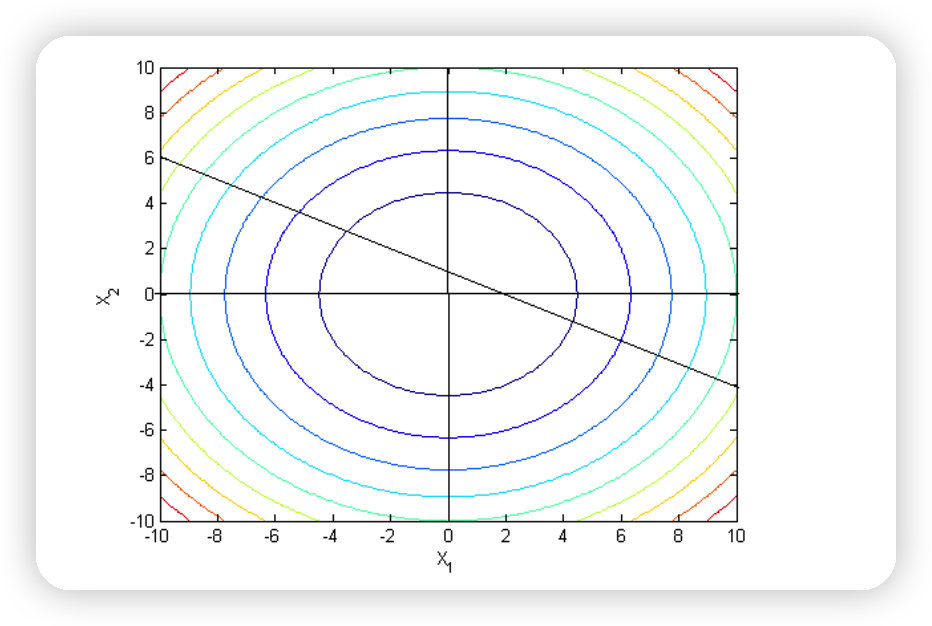
Primal Problem

\(x\)가 (0.4, 0.8)일때, 최소값을 달성한다

( \(f(x^{*}) = f(0.4 ,0.8) = 0.8\) )

Strong duality를 충족함을 보였다!

5. Economic Interpretation

회사 XYZ가 운영비용을 최소화 하고자 한다.

Notation

• \(x\) : 회사 운영 방식

• \(f_0(x)\) : \(x\)와 같이 운영 시의 운영 비용

  ( \(-f_0(x)\) : 이익)

Goal : minimize \(f_0(x)\)

• constraint : \(f_i(x) \leq 0\)

  ( ex. labor, warehouse, environmental … )

Lagrangian

• \(L(x, \lambda)=f_{0}(x)+\sum_{i=1}^{m} \lambda_{i} f_{i}(x)\).

Dual function

• \(g(\lambda)=\min L(x, \lambda)\).