05. Canonical Problems
일반적인 Convex Optimiaztion
- domain set : convex
- objective function ( \(f\) ) : convex
- constraint
- inequality constraint ( \(g_i\) ) : convex
- equality constraint ( \(h_j\) ) : affine
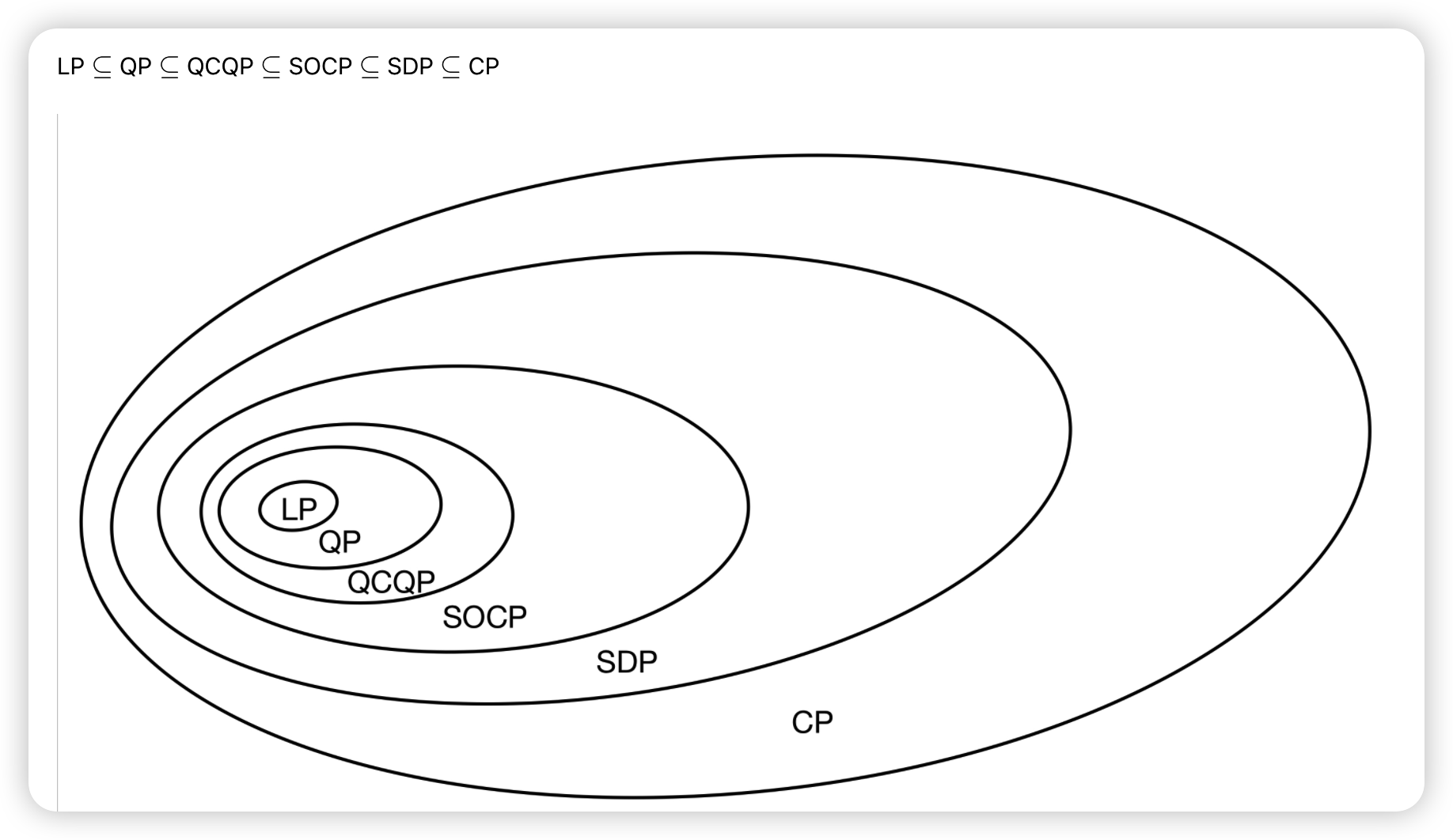
위의 \(f, g_i, h_j\) 의 유형에 따라, optimization problem은, 아래와 같이 6가지로 나뉜다.
- Linear Programming (LP)
- Quadratic Programming (QP)
- Quadratically Constrained Quadratic Programming (QCQP)
- Second-Order Cone Programming (SOCP)
- Semidefinite Programming (SDP)
- Conic Programming (CP)
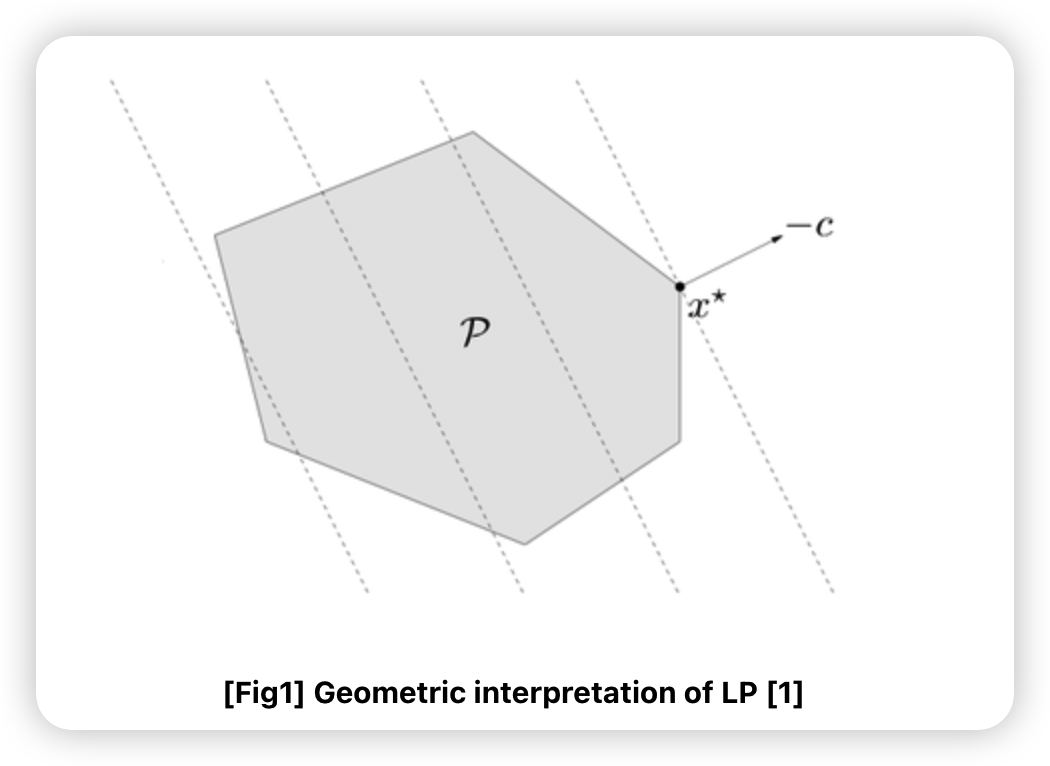
5-1. LP (Linear Programming)
Linear Programming :
- \(f\) : affine
- \(g_i, h_j\) : affine
a) General LP
\(\operatorname{minimize}_{x}\)\(c^{T} x+d\) subject to ..
-
\(G x \preceq h\).
-
\(A x=b\).
where \(G \in \mathbb{R}^{\mathrm{mxn}}\) and \(A \in \mathbb{R}^{\mathrm{pxn}}\).
특징
- \(f\) 의 “+d” 는 constant로 무시 가능
- \(-c^{T} x-d\) 를 minimize 하는 것과 동일
b) LP in standard form
위의 General LP 대신, Standard form LP로 변형할 수 있다.
\(\begin{array}{ll} \operatorname{minimize}_{x} & c^{T} x+d \\ \text { subject to } & A x=b \\ & x \succeq 0 \end{array}\).
[ 변형 과정 ]
Step 1. slack variable \(s\) 사용
- INequality constraint를 equality constraint 로!
\(\begin{array}{ll} \operatorname{minimize}_{x, s} & c^{T} x+d \\ \text { subject to } & G x+s=h \\ & A x=b, \\ & s \succeq 0 . \end{array}\).
Step 2. \(\mathrm{x}\) 를 두 개의 nonnegative variables로 치환
- \(x=x^{+}-x^{-}\), where \(x^{+}, x^{-} \succeq 0\).
\(\begin{array}{ll} \operatorname{minimize}_{x^{+}, x^{-}, s} & c^{T} x^{+}-c^{T} x^{-}+d \\ \text { subject to } & G x^{+}-G x^{-}+s=h \\ & A x^{+}-A x^{-}=b, \\ & s \succeq 0 \\ & x^{+} \succeq 0, x^{-} \succeq 0 . \end{array}\).
Step 3. \(\tilde{x}, \tilde{c}, \tilde{b}, \tilde{A}\) 를 아래와 같이 새롭게 정의
\(\tilde{x}=\left[\begin{array}{c} x^{+} \\ x^{-} \\ s \end{array}\right], \tilde{c}=\left[\begin{array}{c} c \\ -c \\ 0 \end{array}\right], \tilde{b}=\left[\begin{array}{c} h \\ b \end{array}\right], \tilde{A}=\left[\begin{array}{ccc} G & -G & I \\ A & -A & O \end{array}\right]\).
Step 4. Step2의 문제를 \(\tilde{x}, \tilde{c}, \tilde{b}, \tilde{A}\) 로 치환.
\(\begin{array}{ll} \operatorname{minimize}_{\tilde{x}} & \tilde{c}^{T} \tilde{x}+d \\ \text { subject to } & \tilde{A} \tilde{x}=\tilde{b} \\ & \tilde{x} \succeq 0 \end{array}\),
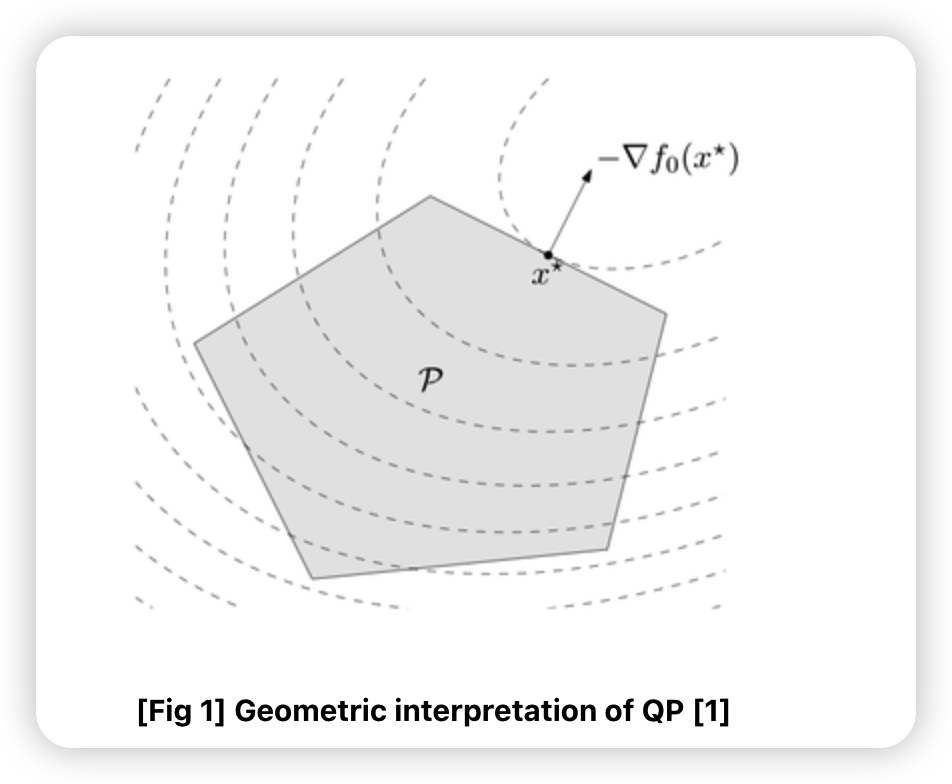
5-2. QP (Quadratic Programming)
Quadratic Programming :
- \(f\) : convex quadratic (2차)
- \(g_i, h_j\) : affine
a) General QP
\(\begin{array}{ll}\operatorname{minimize}_{x} & (1 / 2) x^{T} P x+q^{T} \\ \text { subject to } & G x \preceq h \\ & A x=b\end{array}\) where \(P \in \mathbb{S}_{+}^{n}, G \in \mathbb{R}^{\mathrm{mxn}}\), and \(A \in \mathbb{R}^{\mathrm{pxn}}\)
특징
-
\(f\) 의 “+r” 는 constant로 무시 가능
-
\(P \in \mathbb{S}_{+}^{n}\) 만족 안할 경우, 더 이상 convex problem X
( 따로 명시가 안되어있어도, 당연한 것으로 가정 )
b) QP in standard form
위의 General QP 대신, Standard form QP로 변형할 수 있다.
\(\begin{array}{ll} \operatorname{minimize}_{x} & (1 / 2) x^{T} P x+q^{T} x+r \\ \text { subject to } & A x=b \\ & x \succeq 0 . \end{array}\).
[ 변형 과정 ]
Step 1. slack variable \(s\) 사용
\(\begin{array}{ll} \operatorname{minimize}_{x, s} & (1 / 2) x^{T} P x+q^{T} x+r \\ \text { subject to } & G x+s=h \\ & A x=b, \\ & s \succeq 0 . \end{array}\).
Step 2. \(\mathrm{x}\) 를 두 개의 nonnegative variables로 치환
- \(x=x^{+}-x^{-}\), where \(x^{+}, x^{-} \succeq 0\).
\(\operatorname{minimize}_{x^{+}, x^{-}, s} \quad(1 / 2)\left(x^{+}-x^{-}\right)^{T} P\left(x^{+}-x^{-}\right)+q^{T} x^{+}-q^{T} x^{-}+r\) subject to..
- \(G x^{+}-G x^{-}+s=h\),
- \(A x^{+}-A x^{-}=b\),
- \(s \succeq 0\),
- \(x^{+} \succeq 0, x^{-} \succeq 0\),
Step3. \(\tilde{x}, \tilde{q}, \tilde{b}, \tilde{A}, \tilde{P}\) 를 아래와 같이 새롭게 정의
\(\tilde{x}=\left[\begin{array}{c} x^{+} \\ x^{-} \\ s \end{array}\right], \tilde{q}=\left[\begin{array}{c} q \\ -q \\ 0 \end{array}\right], \tilde{b}=\left[\begin{array}{c} h \\ b \end{array}\right], \tilde{A}=\left[\begin{array}{ccc} G & -G & I \\ A & -A & O \end{array}\right], \tilde{P}=\left[\begin{array}{ccc} P & -P & O \\ -P & P & O \\ O & O & O \end{array}\right]\).
Step4. Step2의 문제를 \(\tilde{x}, \tilde{q}, \tilde{b}, \tilde{A}, \tilde{P}\) 로 치환
\(\begin{array}{ll} \operatorname{minimize}_{\tilde{x}} & (1 / 2) \tilde{x}^{T} \tilde{P} \tilde{x}+\tilde{q}^{T} \tilde{x}+r \\ \text { subject to } & \tilde{A} \tilde{x}=\tilde{b} \\ & \tilde{x} \succeq 0 . \end{array}\).
c) LP & QP의 관계
\(\mathrm{LP} \subseteq \mathrm{QP}\).
- \(QP\)의 \(f\)에서 2차항 제거하면, LP와 동일해짐
Example ) LSE regression
- \(\mid \mid A x-b \mid \mid _{2}^{2}=x^{T} A^{T} A x-2 b^{T} A x+b^{T} b\).
5-3. QCQP (Quadratic Constrained Quadratic Programming)
Quadratic Constrained Quadratic Programming :
- \(f\) : convex quadratic (2차)
- \(g_i\) : convex quadratic (2차)
- \(h_j\) : affine
a) General QP
\(\begin{array}{ll}\operatorname{minimize}_{x} & (1 / 2) x^{T} P_{0} x+q_{0}^{T} x+r_{0} \\ \text { subject to } & (1 / 2) x^{T} P_{i} x+q_{i}^{T} x+r_{i} \leq 0, i=1, \ldots, m \\ & A x=b\end{array}\) where \(P_{i} \in \mathbb{S}_{+}^{n}\) for \(i=0, \ldots, m\), and \(A \in \mathbb{R}^{\mathrm{pxn}}\)
b) QP & QCQP의 관계
\(\mathrm{QP} \subseteq \mathrm{QCQP}\).
- QCQP + ( \(P_{i}=0\), for \(i=1, \ldots, m\) ) = QP
5-4. SOCP (Second Order Cone Programming)
생략
5-5. SDP (Semi-Definite Programming)
생략
5-6. CP (Conic Programming)
생략
