[Explicit DGM] 06. Variants of VAE with Elaborated Losses (1)

[Explicit DGM] 06. Variants of VAE with Elaborated Losses (1)

( 참고 : KAIST 문일철 교수님 : 한국어 기계학습 강좌 심화 2)

Contents

1. Soft SVM
2. $\beta$- VAE
3. ELBO with NN
4. Importance Weighted VAE (IWVAE)

1. Soft SVM

현실의 데이터에 노이즈가 껴 있는 사실을 감안하여, soft SVM에서는 어느 정도의 오차를 허용한다.

이는, 아래의 optimization problem 식을 통해 파악할 수 있다.

Objective : $\min {w, b}|w|+C \sum{j} \xi_{j}$.

Constraint

• $\left(w e_{j}+b\right) y_{j} \geq 1-\xi_{j}, \forall j$.
• $\xi_{j} \geq 0, \forall j$.

위 식에서의 $\xi$는, 허용하는 에러를 의미한다.

목적함수의 $C \sum_{j} \xi_{j}$ term에서 알 수 있듯, 허용하는 오차의 총 합이 loss function에 들어가있다.

그리고 이때 $C$는, 오차를 얼마나 허용할건지에 관한 regularization parameter로 볼 수 있다.

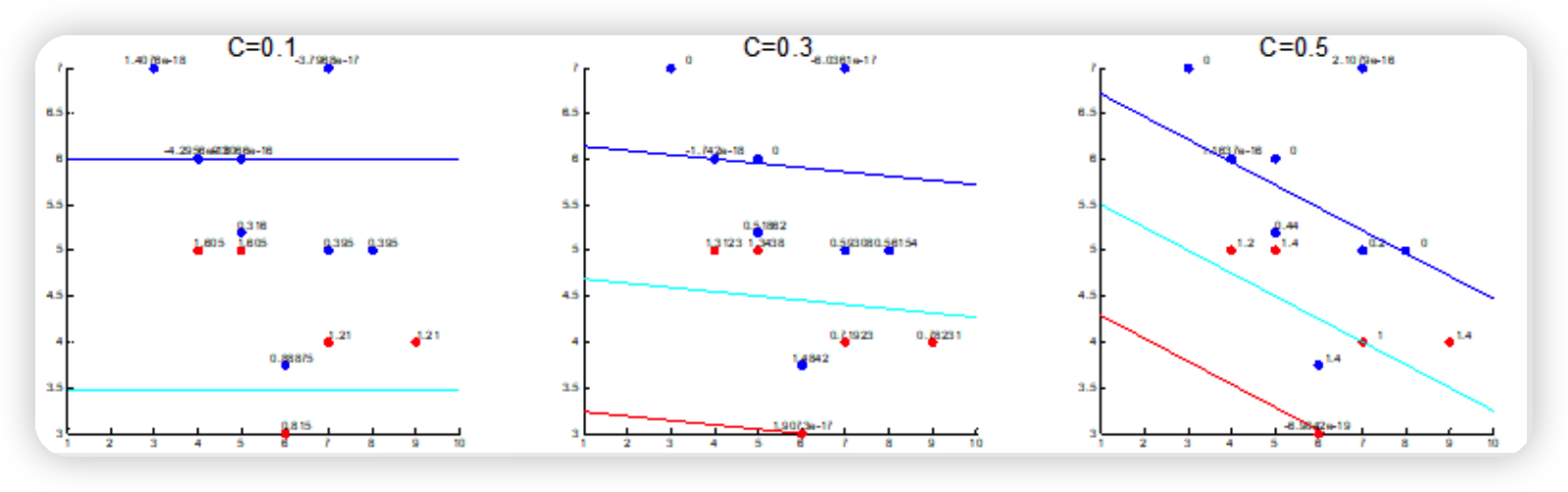
2. $\beta$- VAE

(1) 복습

vanilla VAE의 ELBO 식을 복습해보자. 해당 식은, 아래와 같다.

$\begin{aligned} \ln P(E) &=\ln \sum_{H} P(H, E)\&=\ln \sum_{H} Q(H \mid E) \frac{P(H, E)}{Q(H \mid E)}
& \geq \sum_{H} Q(H \mid E) \ln \left[\frac{P(H, E)}{Q(H \mid E)}\right]\&=-D_{K L}\left(q_{\phi}(H \mid E) | p_{\theta}(H)\right)+\mathbb{E}{q{\phi}}(H \mid E)\left[\log p_{\theta}(E \mid H)\right] \end{aligned}$.

위 ELBO식의 2개의 term을 해석해보자.

• (term 1) $-D_{K L}\left(q_{\phi}(H \mid E) | p_{\theta}(H)\right)$
• (term 2) $\mathbb{E}{q{\phi}}(H \mid E)\left[\log p_{\theta}(E \mid H)\right]$

term 2의 경우에는, 일반적인 (negative) reconstruction error로써 해석할 수 있다.

term 1의 경우에는, variational distn이 prior와 유사하도록 유도하는 regularization term이다.

• 하지만, 우리는 많은 경우에 ( 위의 1.soft SVM에서도 그랬듯 ) 이러한 regularization term이 있으면, 이에 대한 강도(strength)를 조절하고 싶어한다. ( 1.soft SVM에서의 $C$ 처럼 )
• 이를 위해, regularization parameter를 도입한 것이 $\beta-$VAE 라고 보면 된다.

(2) Vanilla VAE vs $\beta$-VAE

Vanilla VAE

• $\max {\phi, \theta} \mathbb{E}{E \sim D}[ -D_{K L}\left(q_{\phi}(H \mid E) | p_{\theta}(H)\right)+\mathbb{E}{q{\phi}}(H \mid E)\left[\log p_{\theta}(E \mid H)\right]]$,

$\beta$-VAE

• $\max {\phi, \theta} \mathbb{E}{E \sim D}\left[\mathbb{E}{H \sim q{\phi}}(H \mid E)\left[\log p_{\theta}(E \mid H)\right]\right]$,

  subject to $D_{K L}\left(q_{\phi}(H \mid E) | p_{\theta}(H)\right)<\epsilon$

위 $\beta$-VAE의 optimization problem을, 라그장스 승수 $\beta$를 도입해서 정리하면 아래와 같다.

$\beta$-VAE의 ELBO를 derive해보면, 아래와 같다.

$F(\phi, \theta, \beta ; E, H)=\mathbb{E}{H \sim q{\phi}(H \mid E)}\left[\log p_{\theta}(E \mid H)\right]-\beta\left(D_{K L}\left(q_{\phi}(H \mid E) | p_{\theta}(H)\right)-\epsilon\right) \\geq \mathbb{E}{H \sim q{\phi}}(H \mid E)\left[\log p_{\theta}(E \mid H)\right]-\beta D_{K L}\left(q_{\phi}(H \mid E) | p_{\theta}(H)\right)$.

위 $\beta$-VAE는, 어떻게 보면 VAE의 generalized version으로 볼 수도 있다.

$\beta$는 regularization hyperparaeter로써,

• $\beta=1 \rightarrow$ Original VAE
• $\beta>1 \rightarrow$ Stronger regularization with $p_{\theta}(H) \sim N(0, I)$

가 된다.

만약 $\beta$가 매우 크다면, variational distn은 diagonal matrix에 가까워질 것이고, 이는 곧 variational parameter들 간의 independence를 유도하게 되는 것으로 해석할 수 있다 ( = Latent disentanglement )

3. ELBO with NN

이번엔, ELBO식을 기존과는 다른 방식으로 정리해볼 것이다.

$\begin{aligned} \mathcal{L}&=-D_{K L}\left(q_{\phi}(H \mid E)\right.\left.| p_{\theta}(H)\right)+\mathbb{E}{q{\phi}(H \mid E)}\left[\log p_{\theta}(E \mid H)\right]
&=\mathbb{E}{q{\phi}(H \mid E)}\left[\log p_{\theta}(E \mid H)\right]+\sum_{H} q_{\phi}(H \mid E)\left[\log p_{\theta}(H)-\log q_{\phi}(H \mid E)\right]
&= \mathbb{E}{q{\phi}(H \mid E)}\left[\log p_{\theta}(E \mid H)+\log p_{\theta}(H)-\log q_{\phi}(H \mid E)\right] \ &=\mathbb{E}{h \sim q(H \mid E, \phi)}\left[\log \frac{p(E, H \mid \theta)}{q(H \mid E, \phi)}\right]\&=\mathbb{E}{\epsilon \sim N(0, I)}\left[\log \frac{p(e, h(\epsilon, e, \lambda) \mid \theta)}{q(h(\epsilon, e, \lambda) \mid e, \phi)}\right] \end{aligned}$.

위 ELBO 식을, MC sampling을 통해 아래와 같이 근사할 수 있다. 그리고, 안에 있는 분수 term을 unnormalized importance weight로 해석할 수도 있다.

$\begin{aligned} \mathcal{L}&= \mathbb{E}{\epsilon \sim N(0, I)}\left[\log \frac{p(e, h(\epsilon, e, \lambda) \mid \theta)}{q(h(\epsilon, e, \lambda) \mid e, \phi)}\right]\& \approx \frac{1}{k} \sum{i=1 . . k} \log \frac{p\left(e, h\left(\epsilon_{i}, e, \lambda\right) \mid \theta\right)}{q\left(h\left(\epsilon_{i}, e, \lambda\right) \mid e, \phi\right)}\&=\frac{1}{k} \sum_{i=1 . . k} \log w\left(e, h\left(\epsilon_{i}, e, \lambda\right) ; \theta_{w}\right) \end{aligned}$,

where $w\left(e, h(\epsilon, e, \lambda), \theta_{w}\right)=\frac{p\left(e, h\left(\epsilon_{i}, e, \lambda\right) \mid \theta\right)}{q\left(h\left(\epsilon_{i}, e, \lambda\right) \mid e, \phi\right)}$ : Unnormalized Importance weight

위 식에서는 $k$개의 $\epsilon$을 샘플했지만, 1개(혹은 여러개)의 $\epsilon$을 샘플해도 된다.

( 더 많은 $k$를 샘플할 수록, 보다 tight한 lower bound를 얻을 수 있다. )

그리고 위 식을 재정리하면, 우리가 애초에 찾고자 했던 Evidence에 대한 lower bound임을 다시 한번 확인할 수 있다.

$\begin{aligned} \mathcal{L}{k}&=\mathbb{E}{h \sim q(H \mid E, \phi)}\left[\log \frac{p(E, H \mid \theta)}{q(H \mid E, \phi)}\right]\&=\mathbb{E}{\epsilon \sim N(0, I)}\left[\log \frac{1}{k} \sum{i=1}^{k} w_{i}\right]
& \leq \log \mathbb{E}{\epsilon \sim N(0, I)}\left[\frac{1}{k} \sum{i=1}^{k} w_{i}\right]\&=\log \mathbb{E}_{h \sim q(H \mid E, \phi)}\left[\frac{p(E, H \mid \theta)}{q(H \mid E, \phi)}\right]=\log p(E) \end{aligned}$.

4. Importance Weighted VAE

위에서 구했듯, ELBO 식은 아래와 같다.

$\mathcal{L}{k}=\mathbb{E}{\epsilon \sim N(0, I)}\left[\log \frac{1}{k} \sum_{i=1}^{k} w_{i}\right]= \mathbb{E}{\epsilon \sim N(0, I)}\left[\log \frac{1}{k} \sum{i=1}^{k} \frac{p\left(e, h\left(\epsilon_{i}, e, \lambda\right) \mid \theta\right)}{q\left(h\left(\epsilon_{i}, e, \lambda\right) \mid e, \phi\right)}\right] $.

위 ELBO를 maximize하기 위해, 이에 대한 미분값을 계산해보자.

$\begin{aligned}\nabla \mathcal{L}{k}&=\nabla \mathbb{E}{\epsilon_{1} \ldots \epsilon_{k}}\left[\log \frac{1}{k} \sum_{i=1}^{k} \frac{p\left(e, h\left(\epsilon_{i}, e, \lambda\right) \mid \theta\right)}{q\left(h\left(\epsilon_{i}, e, \lambda\right) \mid e, \phi\right)}\right]
&=\mathbb{E}{\epsilon{1} \ldots \epsilon_{k}}\left[\nabla_{\theta_{w}} \log \frac{1}{k} \sum_{i=1}^{k} w\left(e, h\left(\epsilon_{i}, e, \lambda\right), \theta_{w}\right)\right]
&=\mathbb{E}{\epsilon{1} \ldots \epsilon_{k}}\left[\frac{\frac{1}{k} \sum_{i=1}^{k} \nabla_{\theta_{w}} w\left(e, h\left(\epsilon_{i}, e, \lambda\right), \theta_{w}\right)}{\frac{1}{k} \sum_{j=1}^{k} w\left(e, h\left(\epsilon_{i}, e, \lambda\right), \theta_{w}\right)}\right]\&=\mathbb{E}{\epsilon{1} \ldots \epsilon_{k}}\left[\sum_{i=1}^{k} \frac{\nabla_{\theta_{w}} w_{i}}{\sum_{j=1}^{k} w_{j}}\right]\&=\mathbb{E}{\epsilon{1} \ldots \epsilon_{k}}\left[\sum_{i=1}^{k} \frac{w_{i} \nabla_{\theta_{w}} \log w_{i}}{\sum_{j=1}^{k} w_{j}}\right]
&=\mathbb{E}{\epsilon{1} \ldots \epsilon_{k}}\left[\sum_{i=1}^{k} \frac{w_{i}}{\sum_{j=1}^{k} w_{j}} \nabla_{\theta_{w}} \log w\left(e, h\left(\epsilon_{i}, e, \lambda\right), \theta_{w}\right)\right] \end{aligned}$.

gradient에 대해 unbiased estimator 를 얻은 것을 알 수 있다!

사용된 trick : log-derivative trick

$\begin{aligned} &\nabla_{\theta} w=w \nabla_{\theta} \log w
&\because \frac{d}{d \theta} \log f(\theta)=\frac{\nabla_{\theta} f(\theta)}{f(\theta)} \end{aligned}$.