[continual] (paper 3) Overcoming catastrophic forgetting by incremental moment matching

Overcoming catastrophic forgetting by incremental moment matching

Contents

1. Abstract
2. Introduction
3. Previous works on Catastrophic Forgetting
   1. Ensemble of NN
   2. Implicit distributed storage of information
   3. Regularization Term
4. Incremental Moment Matching
   1. mean-IMM
   2. mode-IMM
5. Transfer Techniques for IMM
   1. Weight Transfer
   2. L2-Transfer
   3. Drop Transfer
6. Conclusion

0. Abstract

Catastrophic Forgetting

• 새로운 task 학습 과정에서 이전 task 성능 떨어짐 ( weight 손상 )

이 논문은 CF를 극복하기 위한 IMM(Incremental Moment Matching)을 제안함

Neural Network를 task에 대해 “각각” 학습한 뒤, 이를 MoG(Mixture of Gaussian)으로 합침!

Posterior parameter의 search space를 smooth하게 하기 위해…

• 1) Weight Transfer
• 2) L2-Norm
• 3) Variant of Dropout

을 사용한다!

1. Introduction

Catastrophic forgetting은 SGD를 사용하는 모델에서 빈번히 일어나는 문제…

이를 풀고자 하는 continual learning!

최근 들어, REGULARIZATION function을 적용하는 concept이 유행함.

• ex 1) Learning without Forgetting (LwF)

• ex 2) Elastic Weight Consolidation (EWC)

  ( https://seunghan96.github.io/cont/study/study-(continual)(paper-2)Overcoming-Catastrophic-Forgetting-in-NN/ 참고하기! )

이 논문은 EWC의 variant version으로 볼 수 있다!

Incremental Moment Matching (IMM)

• Bayesian NN의 framework를 사용한다

  ( 즉, weight에 uncertainty 부여! weight의 posterior를 계산한다 )

• approximate MoG(Mixture of Gaussian) posterior

  • 각각의 Gaussian은 각각의 task의 NN weight의 posterior

• 서로 다른 posterior를 merge하기 위해, 2가지 MM(moment matching) 방법 사용

  • 1) mean-IMM
    • 단순히 2 NN의 parameter를 average
  • 2) mode-IMM
    • Laplace approximation 사용해서 mode를 approximate

사실 weight를 Gaussian으로 보는 것 자체가 너무 naive

따라서, 아래의 3 transfer learning task를 제안함

• 1) weight transfer
• 2) L2 norm of old&new task
• 3) 새롭게 제안한 variant of dropout

2. Previous works on Catastrophic Forgetting

Catastrophic Forgetting을 해결하기 위한 3가지 큰 방법들

• 1) Ensemble of NN
• 2) Implicit distributed storage of information
• 3) Regularization term

2-1. Ensemble of NN

• 새로운 task올 때마다, 새로운 NN을 형성

• ex) Progressive NN

  ( https://seunghan96.github.io/cont/study/study-(continual)(paper-1)-Progressive-Neural-Network/ 참고! )

• 당연히 complexity issue…. task 수 늘어남에 따라 늘어나게 되는 network의 개수

2-2. Implicit distributed storage of information

• make use of large capacity of NN
• 하지만, extreme change of environment 상황에서는 bad
• 이에 대한 대안으로 제안된 PathNet
  • extend the idea of ensemble approach for parameter reuse within a SINGLE network
  • 알고리즘 간단 소개
    • layer 별 10~20개의 module
    • task 별로, layer별로 3~4개의 module을 pick
  • complexity issue어느 정도 해결!

2-3. Regularization Term

• 앞서 말했듯, 대표적인 2개의 예시

  • 1) LwF (Learning without Forgetting)

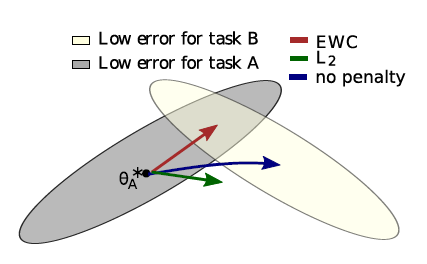
  • 2) EWC (Elastic Weight Consolidation)

    

• [LwF 간단 요약]

  • pseudo-training data from old task를 사용한다

  • 새로운 task학습 이전에, 새로운 task의 데이터를 old task NN에 넣는다.

    거기서 나온 output을 pseudo-label로 사용!

  • new task NN은 아래의 2개의 데이터로 학습

    • new task data
    • old task pseudo-training data

• [EWC 간단 요약]

  • 이전 task로 인해 학습된 posterior distn은, new prior를 update하는데 있어서 사용됨

    이 new prior는 new posterior를 learning하는데에 있어서 사용됨

  • posterior의 covariance matrix가 diagonal 하다고 가정 ( no correlation )

    하지만 그럼에도 불구하고 well working!

3. Incremental Moment Matching

Moments of posterior distn are matched INCREMENTAL way

[ 알고리즘 개요 ]

• posterior를 Gaussian으로 근사함

• \(K\)개의 sequential한 task가 있을 때, 아래의 Gaussian의 parameter들을 찾고자함

  • 1) mean param : \(\mu_{1: K}^{*}\)
  • 2) cov param : \(\Sigma_{1: K_{-}}^{*}\)

  from each \(k\)th task \(\left(\mu_{k}, \Sigma_{k}\right)\)

\(\begin{gathered} p_{1: K} \equiv p\left(\theta \mid X_{1}, \cdots, X_{K}, y_{1}, \cdots, y_{K}\right) \approx q_{1: K} \equiv q\left(\theta \mid \mu_{1: K}, \Sigma_{1: K}\right) \\ p_{k} \equiv p\left(\theta \mid X_{k}, y_{k}\right) \approx q_{k} \equiv q\left(\theta \mid \mu_{k}, \Sigma_{k}\right) \end{gathered}\).

Dimension

• \(\mu_k\) & \(\mu_{1:k}\) : \(D\) 차원
• \(\Sigma_k\) & \(\Sigma_{1:k}\) : \(D \times D\) 차원

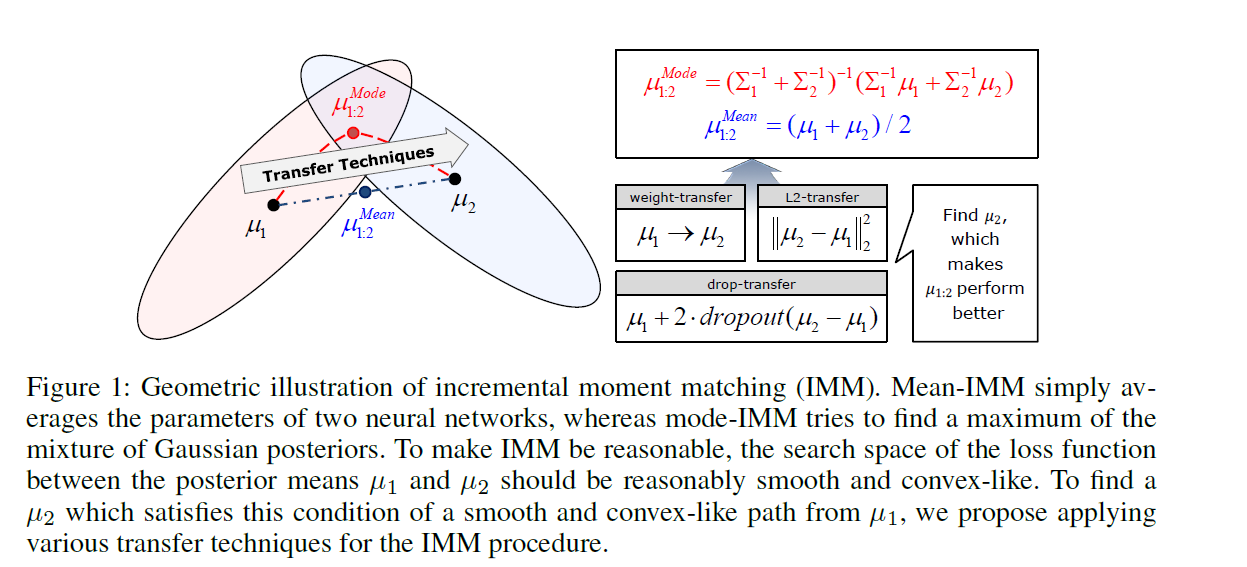
3-1. mean-IMM (Mean-based Incremental Moment Matching)

• 두 개의 NN의 layer 별로 parameter를 (weighted) average 함 ( weight : \(\alpha_k\) )

• objective function of mean-IMM :

  ( 다음의 local KL-divergence를 minimize한다 )

  \(\mu_{1: K}^{*}, \Sigma_{1: K}^{*}=\underset{\mu_{1: K}, \Sigma_{1: K}}{\operatorname{argmin}} \sum_{k}^{K} \alpha_{k} K L\left(q_{k} \mid \mid q_{1: K}\right)\).

• 위 문제를 풀면… optimal solution :

  • \(\mu_{1: K}^{*}=\sum_{k}^{K} \alpha_{k} \mu_{k}\).
  • \(\Sigma_{1: K}^{*}=\sum_{k}^{K} \alpha_{k}\left(\Sigma_{k}+\left(\mu_{k}-\mu_{1: K}^{*}\right)\left(\mu_{k}-\mu_{1: K}^{*}\right)^{T}\right)\).

• 하지만 여기서 covariance matrix는 필요 없음

• shallow NN에서는 자주 사용되어왔다. 이 paper는 DNN에도 적용가능함을 잘 보여줌

3-2. mode-IMM (Mode-based Incremental Moment Matching)

• mean-IMM과 달리, covariance information을 사용한다
• [key idea] posterior를 maximize하는 mode를 찾자!
• mode of MoG with K cluster는 항상 \((K-1)\) dimension의 hypersurface에 존재한다!는 사실을 이용

Laplace Approximation

\(\log q_{1: K} \approx \sum_{k}^{K} \alpha_{k} \log q_{k}+C=-\frac{1}{2} \theta^{T}\left(\sum_{k}^{K} \alpha_{k} \Sigma_{k}^{-1}\right) \theta+\left(\sum_{k}^{K} \alpha_{k} \Sigma_{k}^{-1} \mu_{k}\right) \theta+C^{\prime}\).

Optimal Solution:

• \(\mu_{1: K}^{*}=\Sigma_{1: K}^{*} \cdot\left(\sum_{k}^{K} \alpha_{k} \Sigma_{k}^{-1} \mu_{k}\right)\).

• \(\Sigma_{1: K}^{*}=\left(\sum_{k}^{K} \alpha_{k} \Sigma_{k}^{-1}\right)^{-1}\).

  ( Diagonal Covariance를 가정해서, complexity를 \(O(D^2) \rightarrow O(D)\)로 축소! )

  ( inverse of Fisher Information matrix를 사용한다 )

4. Transfer Techniques for Incremental Moment Matching

일반적으로 NN의 loss function는 non-convex하다.

그렇기 때문에, (당연한거겠지만) 두 NN의 weight를 단순 평균때린게 잘 working할 것이라고 기대할 수 없다!

HOWEVER, 이 논문은 위 문제를 해결하기 위해 다양한 transfer learning technique를 제안한다.

4-1. Weight Transfer

• 이전 task의 weight를 새로운 task의 initial value로써 사용

4-2. L2-Transfer

\(\log p\left(y_{k} \mid X_{k}, \mu_{k}\right)-\lambda \cdot \mid \mid \mu_{k}-\mu_{k-1}\mid \mid_{2}^{2}\).

• variant of L2-regularization
• EWC의 special case로 볼 수 있음
  • prior : Gaussian, with \(\lambda I\) as covariance matrix
• 여기서 사용되는 regularization term은 \(\mu_k\) 와 \(\mu_{k-1}\)의 distance

일반적으로, transfer/continual learning에서는 large \(\lambda\)를 사용하지만,

여기 IMM에서는 small \(\lambda\)를 사용한다

4-3. Drop-transfer

• 이 paper에서 제안한 새로운 방법
• 기존 dropout에서, node를 끄면 zero가 되지만, 여기서는 \(\mu_{k-1}\)이 된다

\[\hat{\mu}_{k, i}=\left\{\begin{array}{ll} \mu_{k-1, i}, & \text { if } i \text { th node is turned off } \\ \frac{1}{1-p} \cdot \mu_{k, i}-\frac{p}{1-p} \cdot \mu_{k-1, i}, & \text { otherwise } \end{array}\right.\]

5. Conclusion

4개의 contribution

• 1) mean-IMM을 continual learning of modern DNN에 ㅈ적용

• 2) mean-IMM을 mode-IMM으로 확장

  ( mode-IMM이 더 성능 good…. covarinace 까지 계산해야한다는 점이 있지만 )

• 3) drop-transfer를 제안

• 4) 그 외의 다양한 transfer technique들을 적용함