[continual] (paper 6) Lifelong Learning with Dynamically Expandable Networks

Lifelong Learning with Dynamically Expandable Networks

Contents

1. Abstract
2. Introduction
3. Incremental Learning of a Dynamically Expandable Network
   1. Algorithm
   2. 세부적 모듈 소개

0. Abstract

Dynamically Expandable Network (DEN)을 제안함

• dynamically decide network capacity, as it trains on sequence of tasks
• trained in an ONLINE manner, by selective retraining

1. Introduction

Lifelong learning = 단지 incremental learning + DL일 뿐

가장 간단한 방법 : (1) FINE-tune

\(\rightarrow\) 하지만, catastrophic forgetting 문제가 있음

그 외의 방법으로, (2) Regularization

• prevents parameters from drastic change!

이 논문에서 제안한 방법은, 위 둘( (1) & (2) )과는 다르다.

RETRAIN the network at each task \(t\), such that each new tasks utilizeis & changes only the RELEVANT part of the PREVIOUS trained netowkr, while still allowing to EXPAND THE NETWORK capacity, when necessary

Challenges

• (1) scalability & efficiency in training
  • retrain에 소요되는 비용이 적게끔 해야
• (2) 언제/얼마나 network를 expand할지
  • 딱 필요한 상황에만, 필요한 만큼만 추가행야
• (3) semantic drift /catastrophic forgetting 방지

이러한 문제들을 극복하기 위해, Dynamically Expandable Networks (DEN)을 제안함

2. Incremental Learning of a Dynamically Expandable Network

Setting

• UNKNOWN number of tasks & distributions of training data
• task \(t\)는 single task일 수도, subtasks들의 모음일 수도 있음
• binary classification task를 가정함
• \(t\) task할때는, \(1 \sim t-1\) task의 데이터는 관측 불가

Life Long learning의 Loss function 기본 틀 :

\(\underset{\boldsymbol{W}^{t}}{\operatorname{minimize}} \mathcal{L}\left(\boldsymbol{W}^{t} ; \boldsymbol{W}^{t-1}, \mathcal{D}_{t}\right)+\lambda \Omega\left(\boldsymbol{W}^{t}\right), \quad t=1, \ldots\).

(1) Algorithm

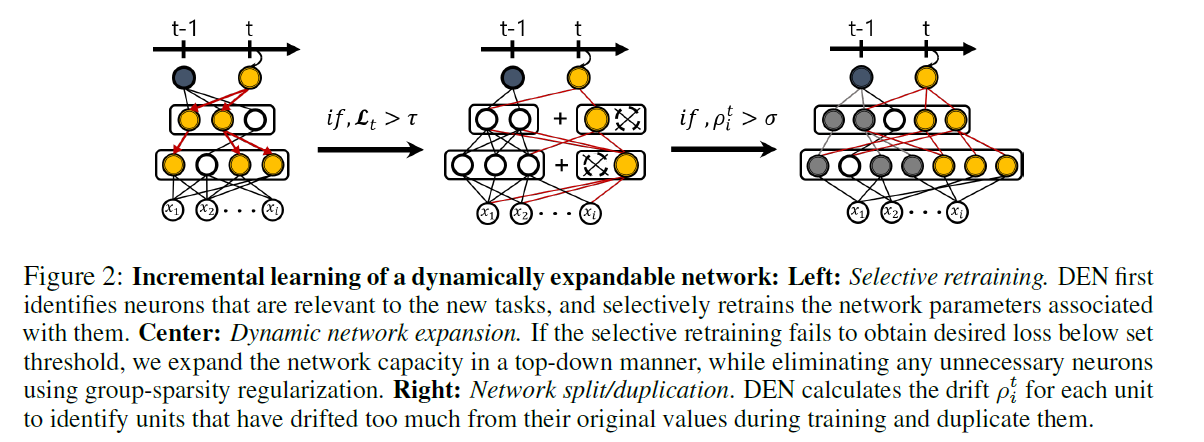
(2) 세부적 모듈 소개

(a) Selective Retraining

• 가장 단순한 방법 ) 새로운 task 올 때마다 계속 전체를 retrain \(\rightarrow\) 너무 COSTLY
• 제안된 방법 ) retrain ONLY the weights, that are affected by new task
  • L-1 regularization 통해 weight에 sparsity 부여
  • 따라서, connected to only few neurons
  • 이를 통해 computational cost 줄일 수 있음
• (\(t=1\)) \(\underset{\boldsymbol{W}^{t=1}}{\operatorname{minimize}} \mathcal{L}\left(\boldsymbol{W}^{t=1} ; \mathcal{D}_{t}\right)+\mu \sum_{l=1}^{L}\left\|\boldsymbol{W}_{l}^{t=1}\right\|_{1}\)
• (새로운 task arrive) \(\underset{\boldsymbol{W}_{L, t}^{t}}{\operatorname{minimize}} \mathcal{L}\left(\boldsymbol{W}_{L, t}^{t} ; \boldsymbol{W}_{1: L-1}^{t-1}, \mathcal{D}_{t}\right)+\mu\left\|\boldsymbol{W}_{L, t}^{t}\right\|_{1}\)
  • obtain the connections between \(o_t\) & hidden units at layer \(L-1\)
  • 이를 통해, train 중 affect 받은 neuron들을 알아낼 수 있음
• train only the weights of the selected sub-network \(S\)
  • \(\underset{\boldsymbol{W}_{S}^{t}}{\operatorname{minimize}} \mathcal{L}\left(\boldsymbol{W}_{S}^{t} ; \boldsymbol{W}_{S^{c}}^{t-1}, \mathcal{D}_{t}\right)+\mu\left\|\boldsymbol{W}_{S}^{t}\right\|_{2}\).

(b) Dynamic Network Expansion

• new task가 previous task와 유사할 경우, 그냥 위처럼 하면 됨

• BUT, 좀 성질이 다른 task라 추가로 parameter가 필요할 수도!

  ( = additional neurons need to be introduced )

  ( selective retraining이후, 일정 threshold 이하로 loss가 떨어지지 않으면 expansion 수행 )

• 이를 위한 효율적인 방법 : group sparse regularization

  • dynamically decide how many neurons to add, at which layer
  • for each task, without repeated retraining

• \(k\)개 unit을 모두 다 합치고 싶지 않으(필요가 없으)니까, 이를 알기 위해 group sparse regularization

  • \(\underset{\boldsymbol{W}_{i}^{N}}{\operatorname{minimize}} \mathcal{L}\left(\boldsymbol{W}_{l}^{\mathcal{N}} ; \boldsymbol{W}_{l}^{t-1}, \mathcal{D}_{t}\right)+\mu\left\|\boldsymbol{W}_{l}^{\mathcal{N}}\right\|_{1}+\gamma \sum_{g}\left\|\boldsymbol{W}_{l, g}^{\mathcal{N}}\right\|_{2}\).

(c) Network Split/Duplication

Semantic Drift ( Catastrophic forgetting )을 방지하기 위한, 제일 대표적인 방법이 regularization

• \(\underset{\boldsymbol{W}^{t}}{\operatorname{minimize}} \mathcal{L}\left(\boldsymbol{W}^{t} ; \mathcal{D}_{t}\right)+\lambda\left\|\boldsymbol{W}^{t}-\boldsymbol{W}^{t-1}\right\|_{2}^{2}\).

• (위 식에서는 \(l_2\) norm 사용했지만, (EWC에서 제안한 것 처럼) Fisher Information 사용해도 OK )

그럼에도 불구하고, task의 성질이 너무 차이나거나, task 수가 너무 많을 경우, 위의 solution은 그닥 좋지 않을 수 있다! 따라서… split the neuron!

• 두 weight가 너무 차이가 많이 나게 되면 ( threshold 이상으로 ), 해당 neuron을 2개로 복사한다.

(기타) Timestamped inference

• network expansion & network split 단계에서 수행

• 새롭게 들어온 neuron(unit)에 index를 제공함으로써, \(\{\boldsymbol{z}\}_{j}=t\)

  나중에 inference time때 자기 task에 맞는 neuron만 사용!