[continual] (paper 8) Progress & Compress ; A scalable framework for continual learning

Progress & Compress : A scalable framework for continual learning

Contents

1. Abstract
2. Introduction
   1. Progress Phase
   2. Compress Phase
3. The Progress and Compress Framework
   1. Learning a New Task ( = Progress Phase )
   2. Distillation and knowledge preservation ( = Compress Phase )
4. Related Work
5. Online EWC
   1. Basic Idea of EWC & 기존의 EWC
   2. Laplace’s approximation to WHOLE posterior
   3. 제안한 Online EWC

0. Abstract

continual learning을 풀기 위한 “Simple & Scalable framework”을 제안함

핵심 : 2개의 NN을 학습시킨다!

• (1) Knowledge base : previous 문제들을 잘 써먹기 위함!
• (2) Active column : current 문제들을 잘 배우기 위함!

위 두개의 NN이 교대로, 아래의 두 과정을 거칠 것임!

• (과정 1) progression
• (과정 2) compression

기타 사항 ( 기존 알고리즘보다 나은 점 )

• architecture 키울 필요 X
• previous data, task 저장 필요 X
• task-specific parameter 따로 필요 X

1. Introduction

대부분의 NN이 푸는 문제들은, 데이터가 i.i.d하다는 가정을 함

\(\rightarrow\) changing environment에 continuously adapt해야하는 system 상에서는 매우 BAD 가정

( = “continual learning 상황에서는 매우 위험한 가정이다” )

5가지 Desiderata for Continual Learning

• (1) catastrophic forgetting X

• (2) positive forward transfer

• (3) positive backward transfer

• (4) scalable

• (5) able to learn without requiring task labels

  ( = 뚜렷히 “어떤 task”이다!를 이야기 못하는 상황에도 잘 풀어야! )

많은 알고리즘들이 위의 5가지 좋은 특징들을 지키고자했음

• ex 1) EWC (Elastic Weight Consolidation)
  • 문제) accumulation of Fisher regulariser \(\rightarrow\) over-constrain NN parameter
• ex 2) Progressive Network
  • 문제) task 올 때 마다 계속 NN을 construct해야 \(\rightarrow\) lack of scalability

이 Paper의 제안

• 두 개의 NN : (1) Knowledge base & (2) Active Column

• 두 개의 과정 : (1) Progress Phase & (2) Compress Phase

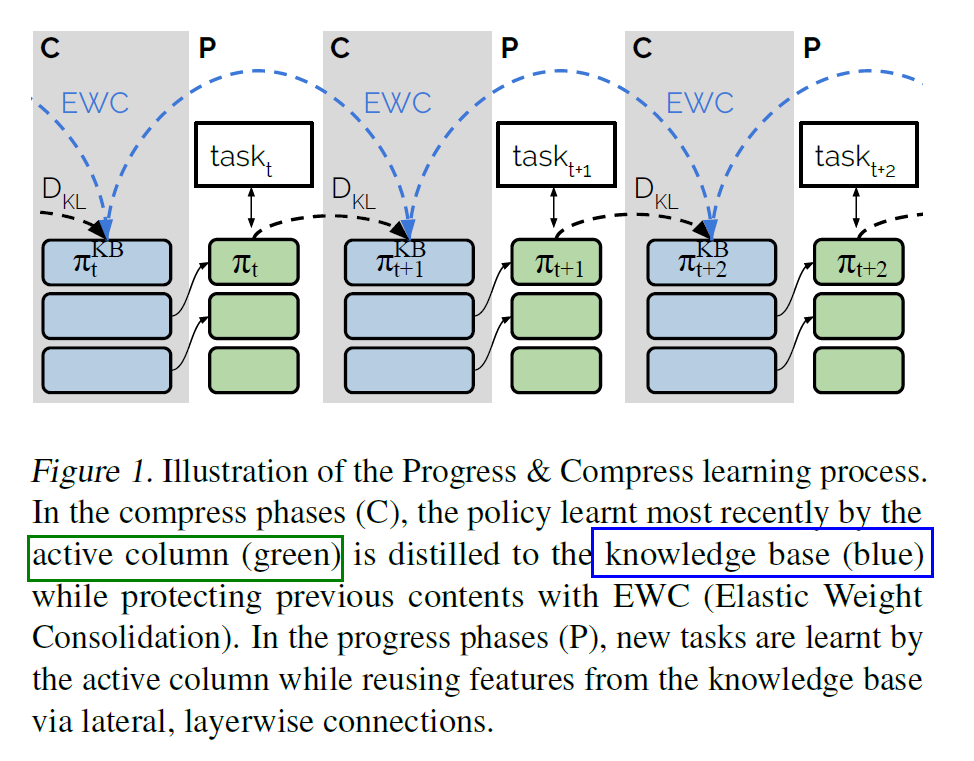
Progress & Compress (P&C) 알고리즘은 위의 두 phase를 교대로 수행한다.

(1) [ Progress Phase ]

• new learning problem이 닥침

• active column의 파라미터만이 update됨

• (Progressive NN에서 착안) layer-wise connection

  • active column & knowledge-base를 연결

    \(\rightarrow\) 이유 : knowledge-base에서 과거 정보 잘 뽑아먹으라고

(2) [ Compress Phase ]

• progress phase 끝난 뒤 수행
• active column을 knowledge base에 distill
• (EWC에서 착안) online EWC
  • 뒤에서 자세히 다룰 것

2. The Progress and Compress Framework

(1) Learning a New Task ( = Progress Phase )

• [fixed] = knowledge base’s 파라미터

  [optimized] = active column’s 파라미터

• 목적 : 과거 정보 잘 활용해서 써먹자

• 아이디어 (방법) : Progressive Nets의 layerwise adaptors

  

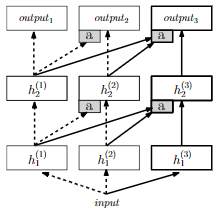
• 수식 ( \(i^{th}\) layer of active column )

  • \(h_{i}=\sigma\left(W_{i} h_{i-1}+\alpha_{i} \odot U_{i} \sigma\left(V_{i} h_{i-1}^{\mathrm{KB}}+c_{i}\right)+b_{i}\right)\).

    ( 여기서 KB notation은 ‘Knowledge-Base’를 의미 ) ( Active Column은 따로 Notation 없음 )

(2) Distillation and knowledge preservation ( = Compress Phase )

• 방금 전에 새로 배운 task의 정보를 knowledge base에 distill하기

• 아이디어 (방법) : EWC (Elastic Weight Consolidation)

• EWC 간단 요약 (복습)

  • (framework) Bayesian solution

  • (핵심) information pretraining to different tasks can be incorporated sequentially into the posterior

  • (문제점) exact posterior X \(\rightarrow\) intractable

  • (해결1) Gaussian (Laplace) Approximation

    \(-\log p\left(\mathcal{T}_{i} \mid \theta\right)+\frac{1}{2} \sum_{j=0}^{i-1} \mid \mid \theta-\theta_{j}^{*} \mid \mid _{F_{j}}^{2}\).

  • (해결1의 문제점) regularizer term이 task의 수에 따라 linear하게 증가

  • (해결2) Online EWC

• 한줄 요약 : 이 논문은 Online EWC를 제안하여 이를 Compress Phase에 사용함

• loss function :

  \(\mathbb{E}\left[\mathrm{KL}\left(\pi_{k}(\cdot \mid x) \| \pi^{\mathrm{KB}}(\cdot \mid x)\right)\right]+\frac{1}{2} \mid \mid \theta^{\mathrm{KB}}-\theta_{k-1}^{\mathrm{KB}} \mid \mid _{\gamma F_{k-1}^{*}}^{2}\).

3. Related Work

( 매우 잘 정리되어 있어서 Good! )

Continual Learning = Lifelong Learning = Never-ending Learning

(1) pre-train model

• catastrophic forgetting이 약해

(2) task-specific parameter

• lack of scalability

(3) Progressive Nteworks

• NN for each column
• lack of scalability

(4) LWF (Learning Without Forgetting)

• (방법) record the output of old task modules on data from the current task, before any update to the shared parameters

• RL에 적용 불가능하다는 문제점

(5) Episodic Memory

• prior task의 example들을 저장 & recall experience
• example 저장 대신, gradient of previous task를 저장하는 방법도!
• MEMORY 과다 \(\rightarrow\) lack of scalability
• (기타) generative model에서 synthetic data 생성

(6) Regularizing Learning

• EWC & Synaptic Intelligence

4. Online EWC

(1) Basic Idea of EWC & 기존의 EWC

• approximate Bayesian Method

• posterior of \(\theta\) :

  \(\begin{aligned} p\left(\theta \mid \mathcal{T}_{1: k}\right) & \propto p(\theta) \prod_{i=1}^{k} p\left(\mathcal{T}_{i} \mid \theta\right) \\ & \propto p\left(\theta \mid \mathcal{T}_{1: k-1}\right) p\left(\mathcal{T}_{k} \mid \theta\right) \end{aligned}\), where \(\mathcal{T}_{1: k}=\left(\mathcal{T}_{1}, \mathcal{T}_{2}, \ldots, \mathcal{T}_{k}\right)\) = data with \(k\) tasks

• 첫 \(k-1\) task 풀고, 이를 prior로써 사용하자!
• intractable 해서 Laplace’s approximation
  • \(p\left(\mathcal{T}_{i} \mid \theta\right) \approx \mathcal{N}\left(\theta ; \theta_{i}^{*}, F_{i}^{-1}\right)\).
  • 최종 loss : \(-\log p\left(\mathcal{T}_{i} \mid \theta\right)+\frac{1}{2} \sum_{j=0}^{i-1} \mid \mid \theta-\theta_{j}^{*} \mid \mid _{F_{j}}^{2}\).

(2) Laplace’s approximation to WHOLE posterior

• 기존의 EWC는 likelihood에 approximation을!

  ( 즉, 매 task 별로 mean & Fisher 다 저장해야하는 burden… )

• (Huszar,2017) Posterior 자체에 Laplace approximation을 하자!

  \(-\log p\left(\mathcal{T}_{i} \mid \theta\right)+\frac{1}{2} \mid \mid \theta-\theta_{i-1}^{*} \mid \mid _{\sum_{j=0}^{i-1} F_{j}}^{2}\).

• 위 식의 특징

  • previous task likelihoods are RE-CENTRED at the latest MAP param \(\theta^{*}_{i-1}\)
  • 마지막 MAP parameter만 저장해도 OK \(\rightarrow\) burden 줄어

• 한계점

  • order task will be remembered less ㅠㅠㅠㅠ

(3) 제안한 Online EWC

• EP (Expectation Propagation) 아이디어 적용

• keep explicit approximation term for each likelihood!

  ( 그럼….결국 다시 기존 EWC처럼 linear scaling 계산 필요한거 아닌가? )

• NO! 하나의 term만 저장하게끔! HOW??

• SOLUTION :

  \(-\log p\left(\mathcal{T}_{i} \mid \theta\right)+\frac{1}{2} \mid \mid \theta-\theta_{i-1}^{*} \mid \mid _{\gamma F_{i-1}^{*}}^{2}\), where \(F_{i}^{*}=\gamma F_{i-1}^{*}+F_{i}\)