(paper 83) The Tunnel Effect; Building Data Representations in Deep Neural NEtworks

The Tunnel Effect: Building Data Representations in Deep Neural NEtworks

Contents

1. Abstract
2. Introduction
3. The Tunnel Effect
   1. Experimental Steup
   2. Main Result
4. Tunnel Effect Analysis
   1. Tunnel Development
   2. Compression and OOD generalization
   3. Network Capacity & Dataset Complexity
5. The Tunenl Effect under Data Distribution Shift
   1. Exploring the effect of task incremental learning on extractor and tunnel
   2. Reducing catastrophic forgetting by adjusting network depth

0. Abstract

DNN : learn more complex data representations.

This paper shows that sufficiently deep networks trained for supervised image classification split into TWO distinct parts that contribute to the resulting data representations differently.

• Initial layers : create linearly separable representations
• Subsequent layers ( = tunnel ) : compress these representations & have a minimal impact on the overall performance.

Explore the tunnel’s behavior ( via empirical studies )

• emerges early in the training process
• depth depends on the relation between the network’s capacity and task complexity.
• tunnel degrades OOD generalization ( + implications for continual learning )

1. Introduction

Consensus : Networks learn to use layers in the hierarchy

• by extracting more complex features than the layers before

  ( = each layer contributes to the final network performance )

\(\rightarrow\) is this really true?

However, practical scenarios :

Deep and Overparameterized NN tend to simplify representations with increasing depth

• WHY?? Despite their large capacity, these networks strive to reduce dimensionality and focus on discriminative patterns during supervised training

\(\rightarrow\) This paper is motivated by these contradictory findings!

How do representations depend on the depth of a layer?

Focuses on severely overparameterized NN

Challenge the common intuition that deeper layers are responsible for capturing more complex and task-specific features

\(\rightarrow\) Demonstrate that DNN split into two parts exhibiting distinct behavior.

Two parts

• FIRST part ( = Extractor ) : builds representations

• SECOND part ( = Tunnel ) : propagates the representations further to the model’s output

  (= compress the representations )

Findings

• (1) Discover Tunnel effect = DNN naturally split into

  • Extractor : responsible for building representations
  • Compressing tunnel : minimally contributes to the final performance.

  Extractor-tunnel split emerges EARLY in training and persists later on

• Show that the tunnel deteriorates the generalization ability on OOD data
• Show that the tunnel exhibits task-agnostic behavior in a continual learning scenario.
  • leads to higher catastrophic forgetting of the model.

2. The Tunnel Effect

Dynamics of representation building in overparameterized DNN

Section Introduction

• (3.1) Tunnel effect is present from the initial stages & persists throughout the training process.

• (3.2) Focuses on the OOD generalization and representations compression.

• (3.3) Important factors that impact the depth of the tunnel.

• (4) Auxiliary question:

  • How does the tunnel’s existence impact a model’s adaptability to changing tasks and its vulnerability to catastrophic forgetting?

    \(\rightarrow\) Main claim : The tunnel effect hypothesis

Tunnel Effect Hypothesis :

Sufficiently large NN develop a configuration in which network layers split into two distinct groups.

• (1) extractor : builds linearly separable representations

• (2) tunnel : compresses these representations

  ( = hinders the model’s OOD generalization )

(1) Experimental setup

a) Architectures

• MLP, VGGs, and ResNets.

• vary the number of layers & width of networks to test the generalizability of results.

b) Tasks

• CIFAR-10, CIFAR-100, and CINIC-10.
  • number of classes: 10 for CIFAR-10 and CINIC-10 and 100 for CIFAR-100,
  • number of samples: 50000 for CIFAR-10 and CIFAR-100 and 250000 for CINIC-10

c) Probe the effects using

• (1) Average accuracy of linear probing
• (2) Spectral analysis of representations
• (3) CKA similarity between representations.

( = Unless stated otherwise, we report the average of 3 runs. )

* Accuracy of linear probing:

• linear classification layer ( train this layer on the classification task )
• measures to what extent \(l\)‘s’ representations are linearly separable.

* Numerical rank of representations:

• compute singular values of the sample covariance matrix for a given layer \(l\) of NN
• estimate the numerical rank of the given representations matrix as the number of singular values above a certain threshold
• can be interpreted as the measure of the degeneracy of the matrix.

* CKA similarity:

• similarity between two representations matrices.
• can identify the blocks of similar representations within the network.

* Inter and Intra class variance:

• Inter-class variance = measures of dispersion or dissimilarity between different classes
• Intra-class variance = measures the variability within a single class

(2) Main Result

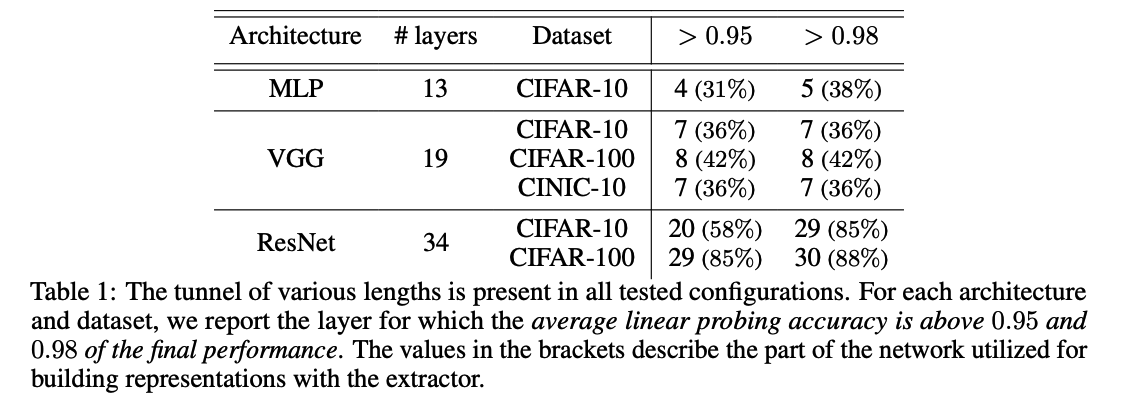
Figure 1 & 2

Early layers of the networks ( = 5 for MLP and 8 for VGG ) are responsible for building linearly-separable representations.

These layers mark the transition between the extractor & the tunnel

For ResNets, the transition takes place in deeper stages of the network ( = 19th layer )

• linear probe performance nearly saturates in the tunnel part, the representations are further refined.

Figure 2

Numerical rank of the representations is reduced to approximately the number of CIFAR-10 classes

For ResNets, the numerical rank is more dynamic,

• exhibiting a spike at 29th layer ( = coincides with the end of the penultimate residual block )

Rank is higher than in the case of MLPs and VGGs.

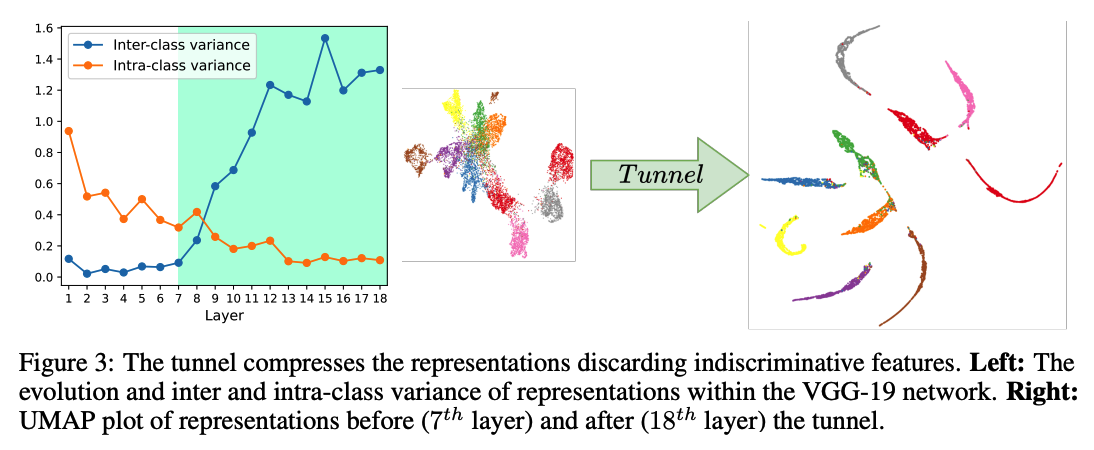
Figure 3

(For VGG-19)

Inter-class variation

• decreases throughout the tunnel

Inter-class variance

• increases throughout the tunnel

Right plot : intuitive explanation of the behavior with UMAP plots

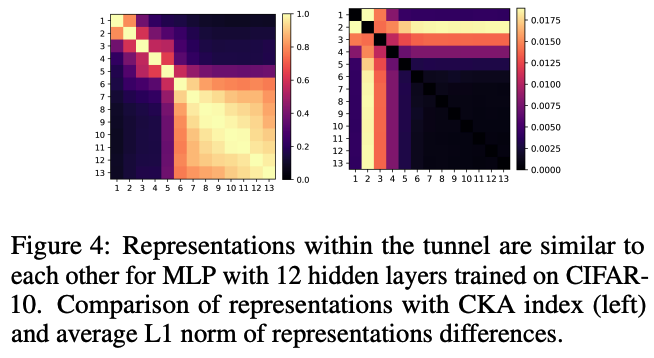
Figure 4

Similarity of MLPs representations using the CKA index & the L1 norm of representations differences between the layers.

• representations change significantly in early layers & remain similar in the tunnel part

3. Tunnel Effect Analysis

Empirical evidence for tunnel effect.

• A) Tunnel develops early during training time

• B) Tunnel compresses the representations & hinders OOD generalization

• C) Tunnel size is correlated with network capacity and dataset complexity

(1) Tunnel Development

a) Motivation

• Understand whether the tunnel is a phenomenon exclusively related to the representations

• Understand which part of the training is crucial for tunnel formation.

b) Experiments

• train VGG19 on CIFAR-10
• checkpoint every 10 epochs

c) Results

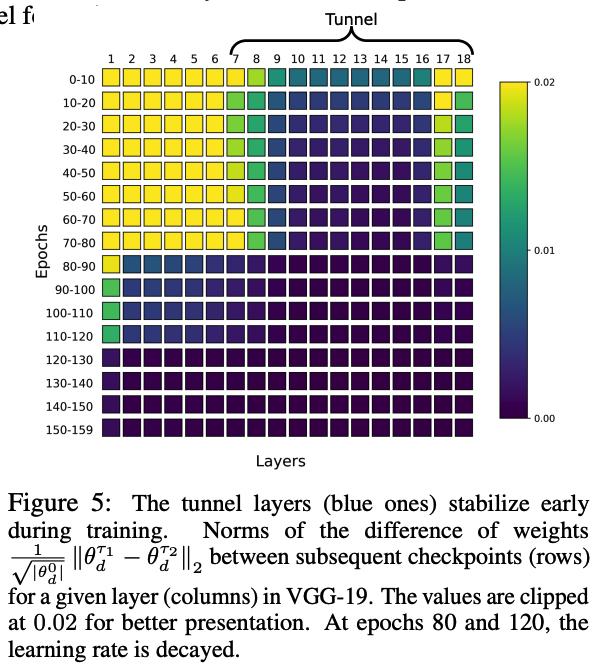
Split between the EXTRACTOR & TUNNEL is also visible in the parameters space.

• at the early stages, and after that, its length stays roughly constant.

  ( = change significantly less than layers from the extractor. )

\(\rightarrow\) Question of whether the weight change affects the network’s final output.

Reset the weights of these layers to the state before optimization.

However, the performance of the model deteriorated significantly.

\(\rightarrow\) Although the change within the tunnel’s parameters is relatively small, it plays an important role in the model’s performance!

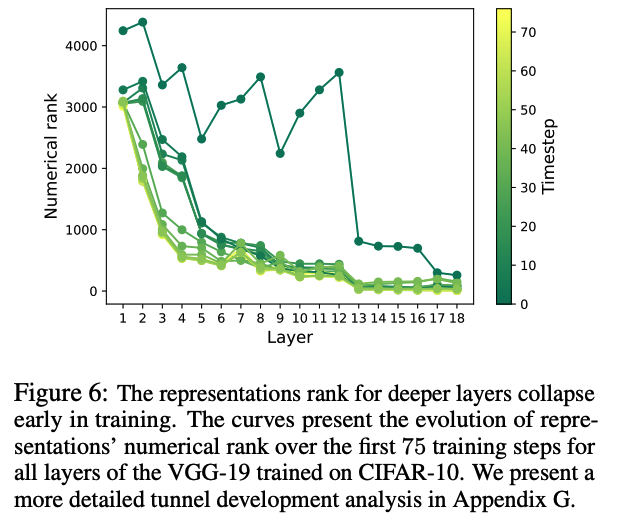
The rank collapses to values near-the-number of classes.

d) Takeaway

• Tunnel formation is observable in the representation and parameter space
• Emerges early in training & persists throughout the whole optimization.
• The collapse in the numerical rank of deeper layers suggest that they preserve only the necessary information required for the task.

(2) Compression and OOD generalization

a) Motivation

Intermediate layers perform better than the penultimate ones for transfer learning … but WHY??

\(\rightarrow\) Investigate whether the tunnel & the collapse of numerical rank within the tunnel impacts the performance on OOD data.

b) Experiments

• architecture : MLPs, VGG-10, ResNet-34
• Source task : CIFAR-10
• Target Task : OOD task ( with linear probes )
  • subset of 10 classes from CIFAR-100
• metric : accuracy of linear probing & numerical rank of representations

c) Results

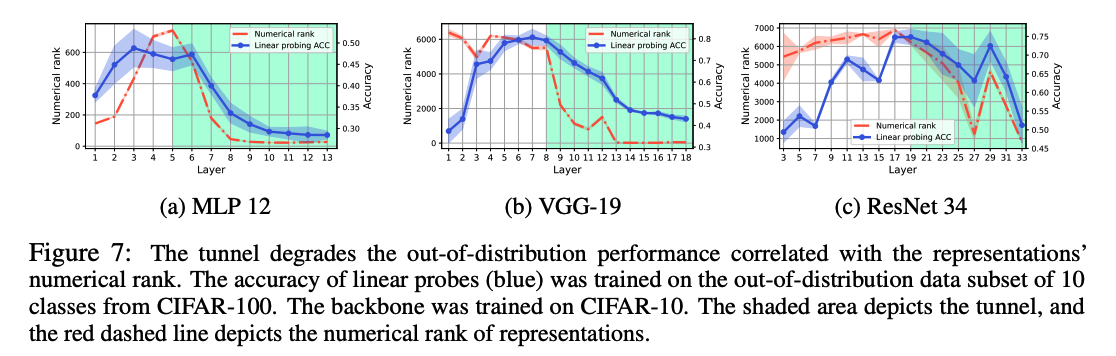
Tunnel is responsible for the degradation of OOD performance

\(\rightarrow\) Last layer before the tunnel is the optimal choice for training a linear classifier on external data.

\(\rightarrow\) OOD performance is tightly coupled with numerical rank of representations

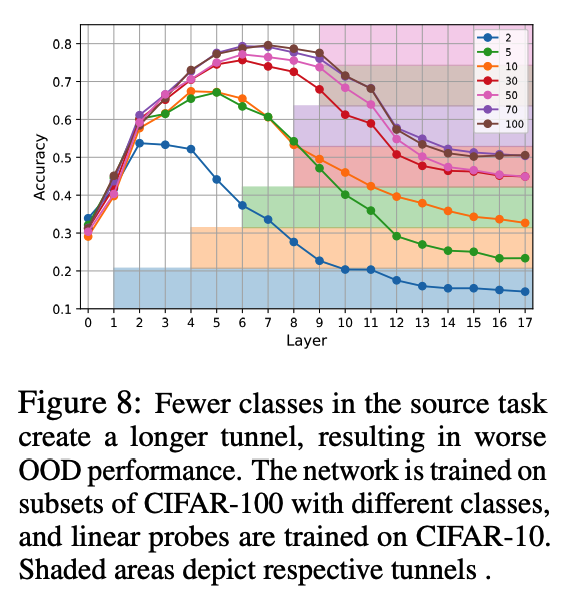
Additional dataset )

• Train a model on different subsets of CIFAR100
• Evaluate it with linear probes on CIFAR-10.

Consistent relationship between the start of the tunnel & the drop in OOD performance.

• Increasing number of classes in the source task \(\rightarrow\) shorter tunnel & later drop in OOD performance.

• Aligns with our earlier findings suggesting that the tunnel is a prevalent characteristic of the model

  ( rather than an artifact of a particular training or dataset setup )

d) Takeaway

Compression of representations ( in the tunnel )

\(\rightarrow\) severely degrades the OOD performance!!

( = by drop of representations rank )

(3) Network Capacity & Dataset Complexity

a) Motivation

Explore what factors contribute to the tunnel’s emergence.

• explore the impact of dataset complexity, network’s depth, and width on tunnel emergence.

b) Experiments

(1) Examine the impact of networks’ depth and width on the tunnel

• using MLPs, VGGs, and ResNets trained on CIFAR-10.

(2) Investigate the role of dataset complexity on the tunnel

• using VGG-19 and ResNet34 on CIFAR-{10,100} and CINIC-10 dataset

c) Results

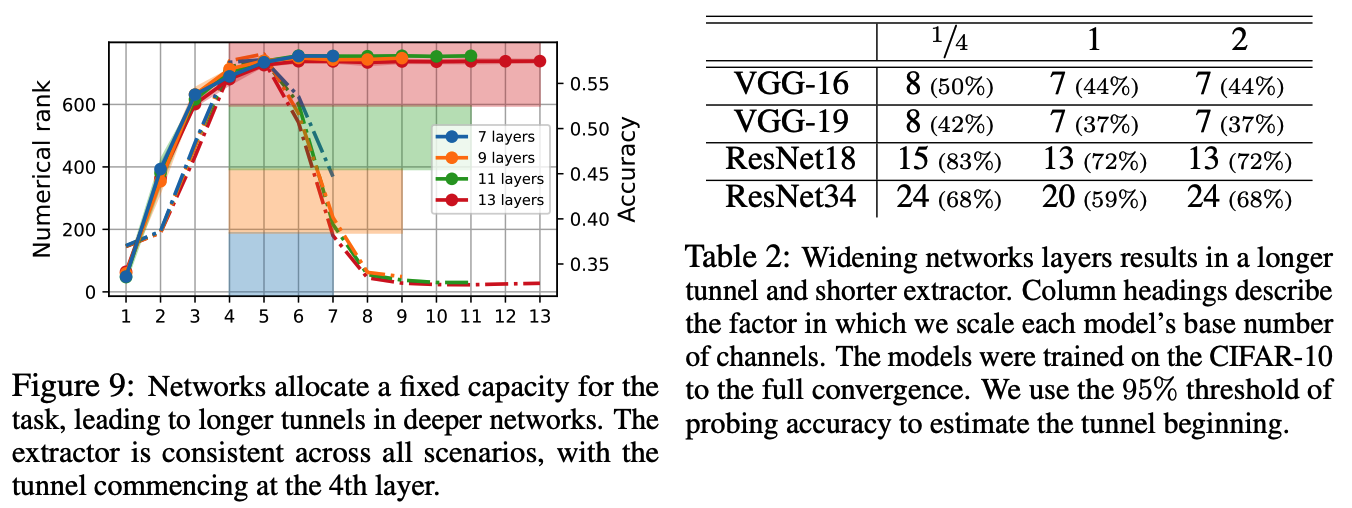
[Figure 9]

Depth of the MLP network has no impact on the length of the extractor part.

\(\rightarrow\) Increasing the network’s depth contributes only to the tunnel’s length!

\(\rightarrow\) Overparameterized NN allocate a fixed capacity for a given task independent of the overall capacity of the model.

[Table 2]

Tunnel length increases as the width of the network grows

( = implying that representations are formed using fewer layers. )

\(\leftrightarrow\) However, this trend does not hold for ResNet34

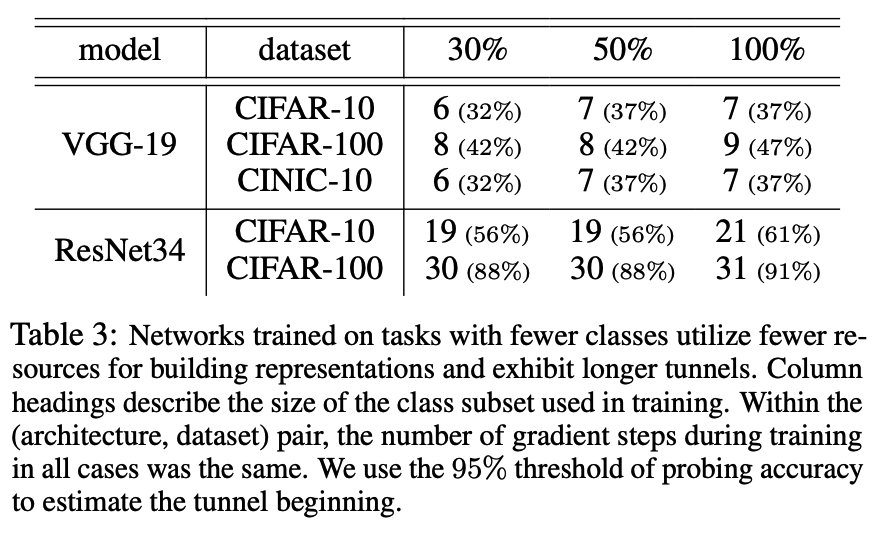
[Table 3]

The number of classes in the dataset directly affects the length of the tunnel.

a) Data size

Even though the CINIC10 training dataset is three times larger than CIFAR-10, the tunnel length remains the same for both datasets.

\(\rightarrow\) Number of samples in the dataset does not impact the length of the tunnel.

b) Number of classes

In contrast, when examining CIFAR-100 subsets, the tunnel length for both VGGs and ResNets increase.

\(\rightarrow\) Clear relationship between the dataset’s number of classes and the tunnel’s length.

d) Takeaway

Deeper or wider networks result in longer tunnels.

& Networks trained on datasets with fewer classes have longer tunnels.

4. The Tunnel Effect under Data Distribution Shift

Investigate the dynamics of the tunnel in continual learning

• large models are often used on smaller tasks typically containing only a few classes.

Focus on understanding the impact of the tunnel effect on ..

• (1) Transfer learning
• (2) Catastrophic forgetting

Examine how the tunnel and extractor are altered after training on a new task.

(1) Exploring the effect of task incremental learning on extractor and tunnel

a) Motivation

Examine whether the extractor and the tunnel are equally prone to catastrophic forgetting.

b) Experiments

• Architecture : VGG-19

• Two tasks from CIFAR-10

  • each task = 5 class

  • Subsequently train on the first and second tasks

    & save the corresponding extractors \(E_t\) and tunnels \(T_t\) , where \(t \in \{1,2\}\) are task numbers

• Separate CLS head for each task

c) Results

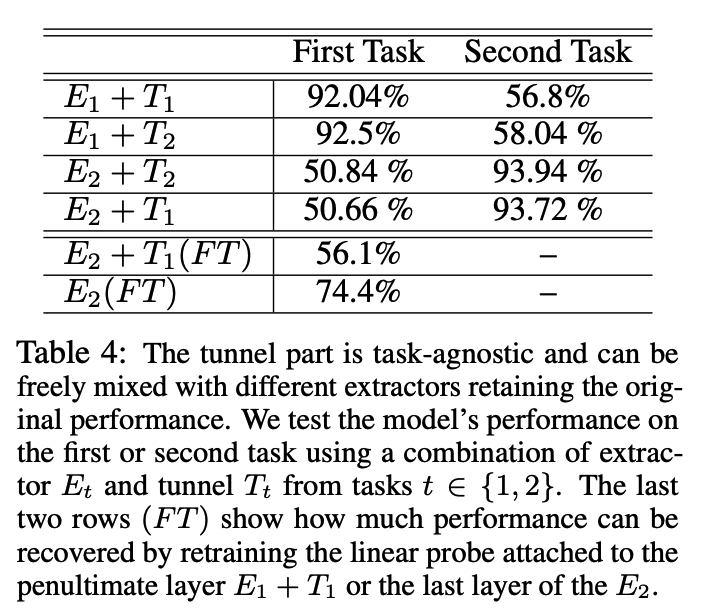
d) Takeaway

The tunnel’s task-agnostic compression of representations provides immunity against catastrophic forgetting when the number of classes is equal.

(2) Reducing Catastrophic Forgetting by adjusting network depth

a) Motivation

Whether it is possible to retain the performance of the original model by training a shorter version of the network.

• A shallower model should also exhibit less forgetting in sequential training.

b) Experiments

• Architecture : VGG-19 networks
  • with different numbers of convolutional layers.
• Each network : trained on two tasks from CIFAR-10.
  • Each task consists of 5 classes

c) Results

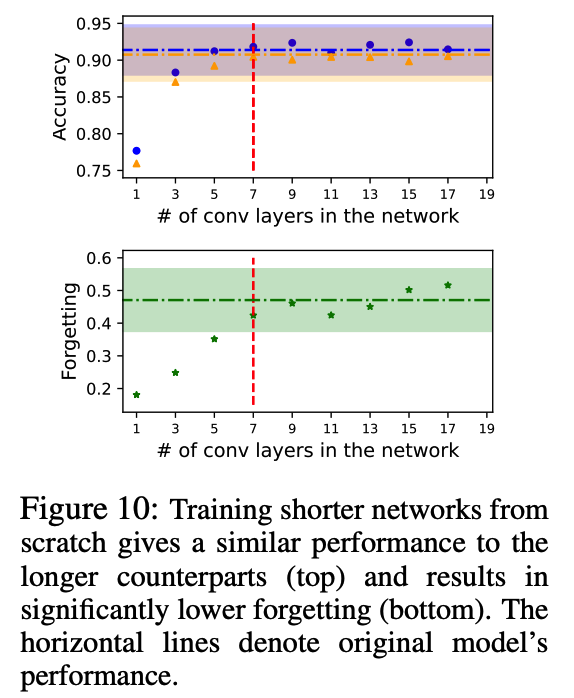
d) Takeaway

Train shallower networks that retain the performance of the original networks & significantly less forgetting.

However, the shorter networks need to have at least the same capacity as the extractor part of the original network.