(paper 83) Rethinking the Value of Labels for Improving Class-Imbalanced Learning

Rethinking the Value of Labels for Improving Class-Imbalanced Learning

Contents

1. Abstract

0. Abstract

Long-tailed dist ( + heavy class imbalance )

Heavily imbalanced data : incurs “label bias” in the classifier

( = decision boundary can be drastically altered by the majority classes )

[ Two facets of labels ]

Class-imbalanced learning can significantly benefit in both SEMI-supervised and SELF-supervised manners.

1. ( Positively ) Imbalanced labels are valuable:
   • given more unlabeled data, the original labels can be leveraged with the extra data to reduce label bias in a semi-supervised manner, which greatly improves the final classifier;
2. ( Negatively ) Imbalanced labels are not useful always:
   • classifiers that are first pre-trained in a self-supervised manner consistently outperform their corresponding baselines.

Rethink the usage of imbalanced labels in realistic long-tailed tasks.

Code is available at https://github.com/YyzHarry/imbalanced-semi-self.

1. Introduction

Imbalanced data … how to solve?

• Data re-sampling approaches [2,5,41]
• Class-balanced losses [7,13,26],

Still…. significant performance drops still remain under extreme class imbalance.

\(\rightarrow\) Need to understand the different characteristics incurred by class-imbalanced learning.

Dilemma on the value of labels:

• (1) Learning algorithms with supervision >. unsupervised
• (2) Imbalanced labels naturally impose “label bias” during learning

\(\rightarrow\) Double-edged sword.

How to maximally exploit the value of labels to improve class-imbalanced learning?

Analyze the 2 facets of imbalanced labels. As our key contributions

• positive view point
• negative view point

Pos & Neg : They can be effectively exploited, in semi-supervised and self-supervised manners respectively!

POSITIVE view

( Theoretically ) simple Gaussian model

• extra unlabeled data benefits imbalanced learning

• substantially improved by employing a simple pseudo-labeling strategy,

  ( = semi-supervised manner r)

NEGATIVE view

Imbalanced labels are NOT advantageous all the time.

( Theoretically ) high-dimensional Gaussian model

• without using labels, with high probability depending on the imbalanceness, we obtain classifier with exponentially small error probability

  ( \(\leftrightarrow\) raw classifier always has constant error )

• Abandon label at the beginning!

  Rather, pre-trained in SSL framework

  • can be greatly compensated through natural self-supervision.

Contributions

1. Systematically analyze imbalanced learning through two facets of imbalanced label,
   • in novel semi- and self-supervised manners.
2. ( Theoretically & Empirically ) Using unlabeled data can substantially boost imbalanced learning through semi-supervised strategies.
3. Introduce SSL for class-imbalanced learning
   • without using any extra data

2. Imbalanced Learning with Unlabeled Data

Scenarios : extra unlabeled data is available

Limited labeling information is critical.

(1) Theoretical Motivation

Binary classification problem

• data distn \(P_{X Y}\) : Mixture of two Gaussians.
  • label \(Y\) : binary ( 1 & -1 ) … with prob 0.5
• \[X \mid Y=+1 \sim \mathcal{N}\left(\mu_1, \sigma^2\right)\]
• \(X \mid Y=-1 \sim \mathcal{N}\left(\mu_2, \sigma^2\right)\).
  • let \(\mu_1>\mu_2\).

Optimal Bayes’s classifier :

• \(f(x)=\operatorname{sign}\left(x-\frac{\mu_1+\mu_2}{2}\right)\),

  ( = Classify \(x\) as +1 if \(x>\left(\mu_1+\mu_2\right) / 2\) )

• measure our ability to learn \(\left(\mu_1+\mu_2\right) / 2\) as a proxy for performance.

Base classifier \(f_B\),

• trained on imbalanced training data

Extra unlabeled data \(\left\{\tilde{X}_i\right\}_i^{\tilde{n}}\)from \(P_{X Y}\) are available,

• study how this affects our performance with the label information from \(f_B\).

Pseudo Labeling

• Pseudo-labeling for \(\left\{\tilde{X}_i\right\}_i^{\tilde{n}}\) using \(f_B\).
• Notation
  • \(\left\{\tilde{X}_i^{+}\right\}_{i=1}^{\tilde{n}_{+}}\) : Unlabeled data whose pseudo-label is +1
  • \(\left\{\tilde{X}_i^{-}\right\}_{i=1}^{\tilde{n}_{-}}\) : Unlabeled data whose pseudo-label is -1

Let \(\left\{I_i^{+}\right\}_{i=1}^{\tilde{n}_{+}}\)be the indicator that the \(i\)-th pseudo-label is correct,

• if \(I_i^{+}=1\), then \(\tilde{X}_i^{+} \sim \mathcal{N}\left(\mu_1, \sigma^2\right)\)

  • assume \(I_i^{+} \sim \operatorname{Bernoulli}(p)\),

    ( = means \(f_B\) has an accuracy of \(p\) for the positive class )

• if \(I_i^{-}=1\), then \(\tilde{X}_i^{-} \sim \mathcal{N}\left(\mu_2, \sigma^2\right)\)

  • assume \(I_i^{-} \sim \operatorname{Bernoulli}(q)\)

    ( = means \(f_B\) has an accuracy of \(q\) for the negative class )

Imbalance in accuracy : \(\Delta \triangleq p-q\)

Aim to learn \(\left(\mu_1+\mu_2\right) / 2\) with the above setup, via the extra unlabeled data

It is natural to construct our estimate as…

• \(\hat{\theta}=\frac{1}{2}\left(\sum_{i=1}^{\tilde{n}_{+}} \tilde{X}_i^{+} / \tilde{n}_{+}+\sum_{i=1}^{\tilde{n}_{-}} \tilde{X}_i^{-} / \tilde{n}_{-}\right)\).

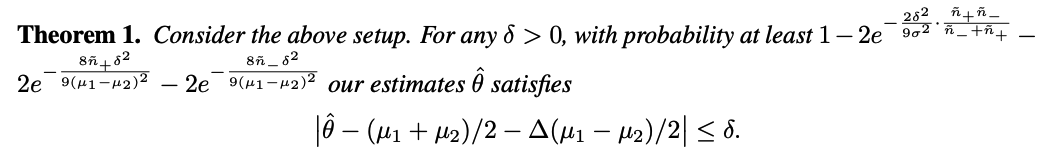
Interpretation.

(1) Training data imbalance affects the accuracy of our estimation.

• Heavily imbalanced training data :

  \(\rightarrow\) Large difference in accuracy between major & minor classes.

  \(\rightarrow\) The more imbalanced, the larger the gap \(\Delta\)

(2) Unlabeled data imbalance affects the probability of obtaining such a good estimation.

• Reasonably good base classifier :
  • we can roughly view \(\tilde{n}_{+}\)and \(\tilde{n}_{-}\) as approximations for the number of actually positive and negative data in unlabeled set.
• Term \(2 \exp \left(-\frac{2 \delta^2}{9 \sigma^2} \cdot \frac{\tilde{n}_{+} \tilde{n}_{-}}{\tilde{n}_{-}+\tilde{n}_{+}}\right)\),
  • \(\frac{\tilde{n}_{+} \tilde{n}_{-}}{\tilde{n}_{-}+\tilde{n}_{+}}\)is maximized when \(\tilde{n}_{+}=\tilde{n}_{-}\), ( = balanced unlabeled data )

Probability of success would be higher with balanced data, but in any case, more unlabeled data is always helpful.

(2) Semi-supervised Imbalanced Learning Framework

Pseudo-label can be helpful in imbalanced learning !!

( How much useful ?? Depends on the imbalanceness of the data )

Probe the effectiveness of unlabeled data

a) Semi-Supervised Imbalanced Learning

Classic self-training framework

adopt Semi-SL by generating pseudo-labels for unlabeled data.

• step 1) Intermediate classifier \(f_{\hat{\theta}}\) : via original imbalanced dataset \(\mathcal{D}_L\),
• step 2) Generate pseudo-labels \(\hat{y}\) for unlabeled data \(\mathcal{D}_U\).
• step 3) Combine data & pseudo-labels \(\rightarrow\) Final model \(f_{\hat{\theta}_{\mathrm{f}}}\)
  • by minimizing \(\mathcal{L}\left(\mathcal{D}_L, \theta\right)+\omega \mathcal{L}\left(\mathcal{D}_U, \theta\right)\), where \(\omega\) is the unlabeled weight.

Remodel the class distribution with \(\mathcal{D}_U\),

• obtaining better class boundaries especially for tail classes.

• more advanced Semi-SL techniques can be easily incorporated

  ( just by modifying only the loss function )

Demonstrate the value of unlabeled data

• a simple self-training procedure can lead to substantially better performance for imbalanced learning.

b) Experimental Setup.

Dataset : Artificially created long-tailed versions of CIFAR-10 & SVHN

• Unlabeled part with similar distributions:
  • CIFAR-10 : 80 Million Tiny Images
  • SVHN : own extra set

Class imbalance ratio \(\rho\)

• definition = # of HEAD class / # of TAIL class
  • HEAD class : most frequent
  • TAIL class : least frequent

Unlabeled imbalance ratio \(\rho_U\)

• \(\rho\) for \(\mathcal{D}_U\), ( define the same way )

For long-tailed dataset with a fixed \(\rho\), we augment it with 5 times more unlabeled data,

\(\rightarrow\) denoted as \(\mathcal{D}_U @ 5 \mathrm{x}\).

• the total size of \(\mathcal{D}_U @ 5 \mathrm{x}\) is fixed
• vary \(\rho_U\) to obtain corresponding imbalanced \(\mathcal{D}_U\).

Etc )

• Cross-entropy (CE) training … least the better
• Baseline : LDAM-DRW

2-1) Main Results

CIFAR-10-LT & SVHN-LT

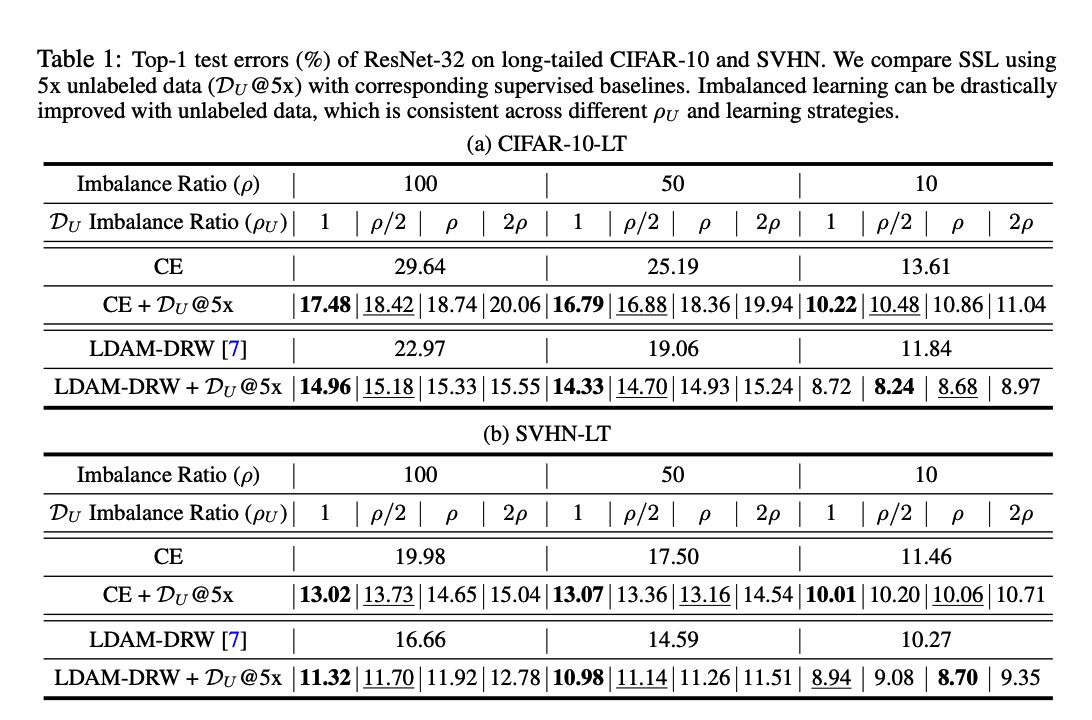
Imbalanced Distn in Unlabeled Data

“Unlabeled data imbalance” affects the learning of final classifier.

• With smaller \(\rho_U\) (i.e., more balanced \(\mathcal{D}_U\) ) leading to larger gains.
• However, as the original dataset becomes more balanced, the benefits from \(\mathcal{D}_U\) tend to be similar across different \(\rho_U\).

Qualitative Results.

visualize representations learned with..

• vanilla CE (Fig. 1a)
• Semi-SL (Fig. 1b)

Imbalanced training set

\(\rightarrow\) Poor class separation, particularly for TAIL classes,

Leveraging unlabeled data

\(\rightarrow\) Boundary of TAIL classes can be better shaped,

Summary : POSITIVENESS of unlabeled data

• class-imbalanced learning tasks benefit greatly from additional unlabeled data

3. A Closer Look at Unlabeled Data under Class Imbalance

Section 2 : Value of imbalanced labels with extra unlabeled data.

Question : Is Semi-SL is the solution to practical imbalanced data.??

NOT REALLY !!

• Semi-SL can be problematic in certain scenarios when the unlabeled data is not ideally constructed.

• Techniques are often sensitive to the relevance of unlabeled data
• Can even degrade if the unlabeled data is largely mismatched
• Unlabeled data could also exhibit long-tailed distributions !!

\(\rightarrow\) Probe the utility of Semi-SL techniques.

a) Data Relevance under Imbalance.

Construct sets of unlabeled data

• with the same imbalance ratio ( as the training data )
• BUT varying relevance

Details :

• Mix the original unlabeled dataset with irrelevant data
• Create unlabeled datasets with varying data relevance ratios

Results

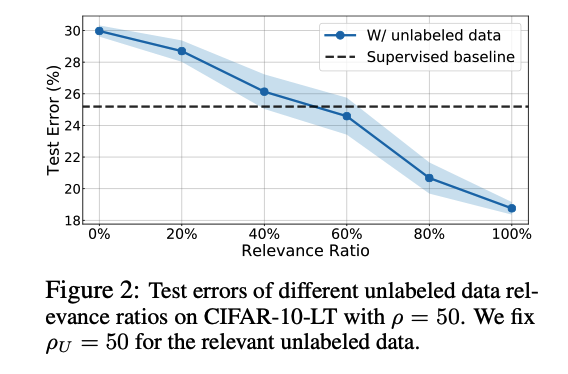
[ Figure 2 ]

• Adding unlabeled data from MISmatched classes can actually HURT performance

• Relevance has to be as high as 60% to be effective

• observations are consistent with the balanced cases

b) Varying \(\rho_U\) under Sufficient Data Relevance

Even with enough relevance ….

What if the relevant unlabeled data is (heavily) LONG-TAILED?

Results

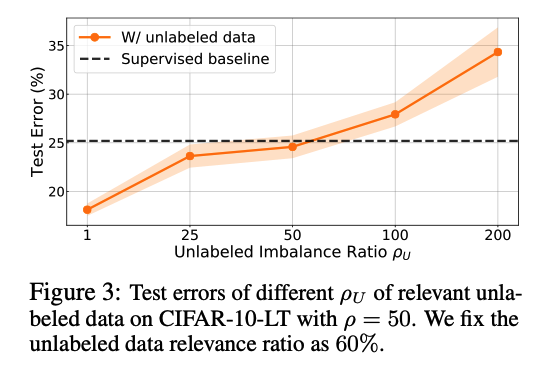
[ Figure 3 ]

• ( Fixed relevance ) Higher \(\rho_U\) , the higher the test error.
• \(\rho_U\) should be at most 50 ( = imbalance ratio of the training data ).

\(\rightarrow\) Unlike traditional setting, the imbalance of the unlabeled data imposes an additional challenge.

c) Why Do These Matter?

Semi-SL techniques should be applied with care

Relevant case : OK

Non-relevant case : BE CAREFUL!

• ex) Medical diagnosis : positive samples are always scarce
  • confounding issues (e.g., other disease or symptoms) undoubtedly hurt relevance.

Summary

• Unlabeled data are useful.
• HOWEVER … Semi-SL alone is not sufficient!!

4. Imbalanced Learning from Self-Supervision

Next Question

Can the negative viewpoint of the dilemma ( = the imbalanced labels introduce bias and hence are “unnecessary” ) , be successfully exploited as well to advance imbalanced learning?

Our goal is to seek techniques that can be broadly applied WITHOUT extra data

\(\rightarrow\) usage of SSL

(1) Theoretical Motivation

How imbalanced learning benefits from SSL?

Notation

• \(d\)-dimensional binary classification
• Data generating distribution \(P_{X Y}\) : Mixture of Gaussians.
• Labels
  • \(Y=+1\) with probability \(p_{+}\)
  • \(Y=-1\) with probability \(p_{-}=1-p_{+}\).
• Majority & Minority
  • Let \(p_{-} \geq 0.5\) ( = major class is negative )

Data Generation

• \(X \mid Y=+1 \sim \mathcal{N}\left(0, \sigma_1^2 \mathbf{I}_d\right)\).

• \(X \mid Y=-1 \sim \mathcal{N}\left(0, \beta \sigma_1^2 \mathbf{I}_d\right)\) for some constant \(\beta>3\)

  ( = negative samples have larger variance )

Training data, \(\left\{\left(X_i, Y_i\right)\right\}_{i=1}^N\), could be highly imbalanced

• # of positive : \(N_{+}\)
• # of negative : \(N_{-}\)

Learning a linear classifier w/ & w/o SSL

• class of linear classifiers \(f(x)=\operatorname{sign}(\langle\theta\), feature \(\rangle+b)\),
  • For convenience, we consider the case where the intercept \(b \geq 0\).
• SL vs SSL
  • SL : raw input \(X\)
  • SSL : \(Z=\psi(X)\) for some representation \(\psi\) learned via SSL

Black-box SSL task

• learned representation is \(Z=k_1\mid \mid X \mid \mid_2^2+k_2\), where \(k_1, k_2>0\).

  ( = without knowing explicitly what the transformation \(\psi\) is. )

Measure the performance of a classifier \(f\)

• using the standard error probability
• \(\operatorname{err}_f=\mathbb{P}_{(X, Y) \sim P_{X Y}}(f(X) \neq Y)\).

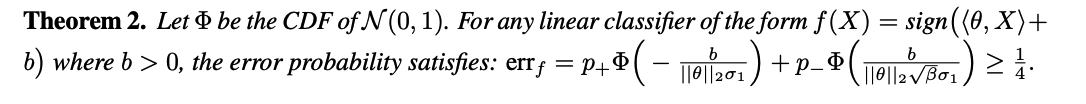
• SL ) Whether imbalanced or not, linear classifier cannot have an accuracy \(\geq 3 / 4\).
• SSL ) \(Z\) provides a better classifier.
  • Consider the same linear class \(f(x)=\operatorname{sign}(\langle\theta\), feature \(\rangle+b), b>0\)
  • Explicit classifier with feature \(Z=\psi(X)\)
    • \(f_{s s}(X)=\operatorname{sign}(-Z+b), b=\frac{1}{2}\left(\frac{\sum_{i=1}^N 1_{\left\{Y_i=+1\right\}} Z_i}{N_{+}}+\frac{\sum_{i=1}^N 1_{\left\{Y_i=-1\right\}} Z_i}{N_{-}}\right)\).
  • High probability error bound for the performance of this linear classifier.

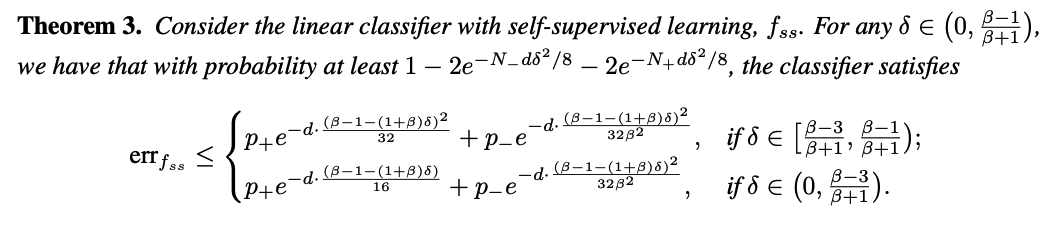
Interpretation ( Theorem 3 )

By first abandoning imbalanced labels & learn via SSL…

• (1) With high probability, we obtain a satisfying classifier \(f_{s s}\), whose ((error probability decays exponentially on the dimension \(d\).

  • The probability of obtaining such a classifier also depends exponentially on \(d\) and the number of data.

    ( Note : Modern data is of extremely high dimension ! )

  • Even for imbalanced data, one could obtain a good classifier with proper SSL

• (2) Training data imbalance affects our probability of obtaining such a satisfying classifier.

  • Given \(N\) data, if it is highly imbalanced ( = extremely small \(N_{+}\) )

    \(\rightarrow\) term \(2 \exp \left(-N_{+} d \delta^2 / 8\right)\) could be moderate & dominate \(2 \exp \left(-N_{-} d \delta^2 / 8\right)\).

  • With more data ( regardless of balance ) probability of success increases.

(2) Self-supervised Imbalanced Learning Framework

How SSL can help class-imbalanced tasks?

Self-Supervised Imbalanced Learning.

• Abandon the label information
• Step 1) Perform self-supervised pre-training (SSP).
  • learn better initialization ( more label-agnostic ) from the imbalanced dataset.
• Step 2) Perform any standard training approach
  • pre-training is independent of the learning approach
  • compatible with any existing imbalanced learning techniques.

SSP can be easily embedded with existing techniques,

\(\rightarrow\) Any base classifiers can be consistently improved using SSP!!

Experimental Setup

Datasets

• CIFAR-10-LT and CIFAR- 100-LT

• ( large-scale long-tailed datasets ) ImageNet-LT & iNaturalist 2018

Evaluation

• corresponding balanced test datasets

SSP method :

• (a) Rotation : on CIFAR-LT
• (b) MoCo : on ImageNet-LT and iNaturalist

Epochs

• 200 epochs on CIFAR-LT
• 90 epochs on ImageNet-LT and iNaturalist

2-1) Main Results

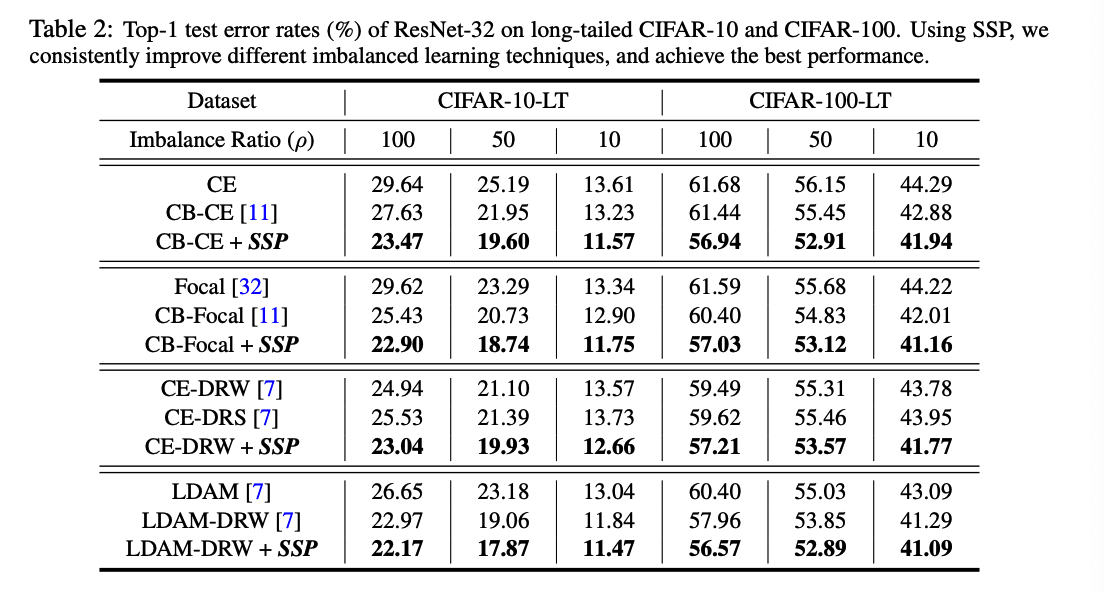
CIFAR-10-LT & CIFAR-100-LT

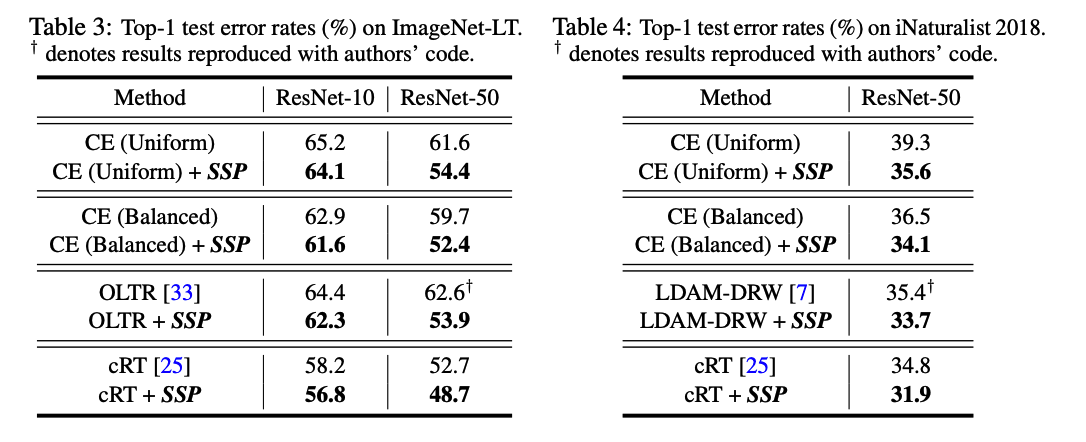
ImageNet-LT & iNaturalist 2018

Qualitative Results

5. Related Work

(1) Imbalanced Learning & Long-tailed Recognition.

Classical methods

• designing data re-sampling strategies
  • ex) over-sampling the minority classes
  • ex) under-sampling the frequent classes
• cost-sensitive re-weighting schemes
  • adjust weights during training for different classes or even different samples.

Other methods

• class-balanced losses
  • consider intra- or inter-class properties
• transfer learning
• metric learning
• meta-learning

Recent studies

• decoupling the representation and classifier leads to better long-tailed learning results.

This paper : provide systematic strategies through 2viewpoints of imbalanced labels, which boost imbalanced learning

• in both (1) Semi-SL and (2) SSL

(2) Semi-Supervised Learning.

Learning from both unla- beled and labeled samples

Categories

• entropy minimization
• pseudo- labeling

• generative models

• consistency-based regularization
  • consistency loss is integrated to push the decision boundary to low-density areas using unlabeled data

Common evaluation protocol

• assumes the unlabeled data comes from the same or similar distributions as labeled data

  ( \(\leftrightarrow\) may not reflect realistic settings )

(3) Self-Supervised Learning.

PASS