CReST: A Class-Rebalancing Self-Training Framework for Imbalanced Semi-Supervised Learning
Contents
- Abstract
- Introduction
- Related Work
- Semi-SL
- Class-imbalanced SL
- Class-imbalanced Semi-SL
- Class-imbalanced Semi-SL
- Problem setup and baselines
- A closer look at the model bias
- Class-rebalancing self-training
- Progressive Distribution Alignment
- Experiments
- CIFAR-LT
- ImageNet127
- Ablation Study
0. Abstract
[ Semi-SL on Imbalanced Data ]
Existing Semi-SL methods :
-
perform poorly on minority classes
-
still generate high precision pseudo-labels on minority classes.
Class- Rebalancing Self-Training (CReST),
- Simple yet effective framework to improve existing Semi-SL methods on class imbalanced data.
- Iteratively retrains a baseline Semi-SL model with a labeled set expanded by adding pseudo-labeled samples from an unlabeled set
- pseudo-labeled samples from minority classes are selected more frequently according to an estimated class distribution.
- CResT+ : a progressive distribution alignment to adaptively adjust the rebalancing strength
1. Introduction
Semi-SL’s common assumption
= the class distribution of labeled and/or unlabeled data are balanced
\(\rightarrow\) Not in reality!
Supervised Leanring (on imbalanced data)
-
biased towards majority classes
-
various solutions have been proposed to help alleviate bias
- ex) re-sampling, re-weighting, two-stage training
\(\rightarrow\) rely on labels to rer-balance the biased model
Semi-SL (on imbalanced data)
-
has been under-studied
- data imbalance poses further challenges in Semi-SL
- missing label information precludes rebalancing the unlabeled set.
- Pseudo-labeling
- label for unlabeled data generated by a model trained on labeled data
- problematic if they are generated by an initial model trained on imbalanced data
- Majority of existing Semi-SL algorithms have not been evaluated on imbalanced data distributions.
This paper : Semi-SL under class-imbalanced data
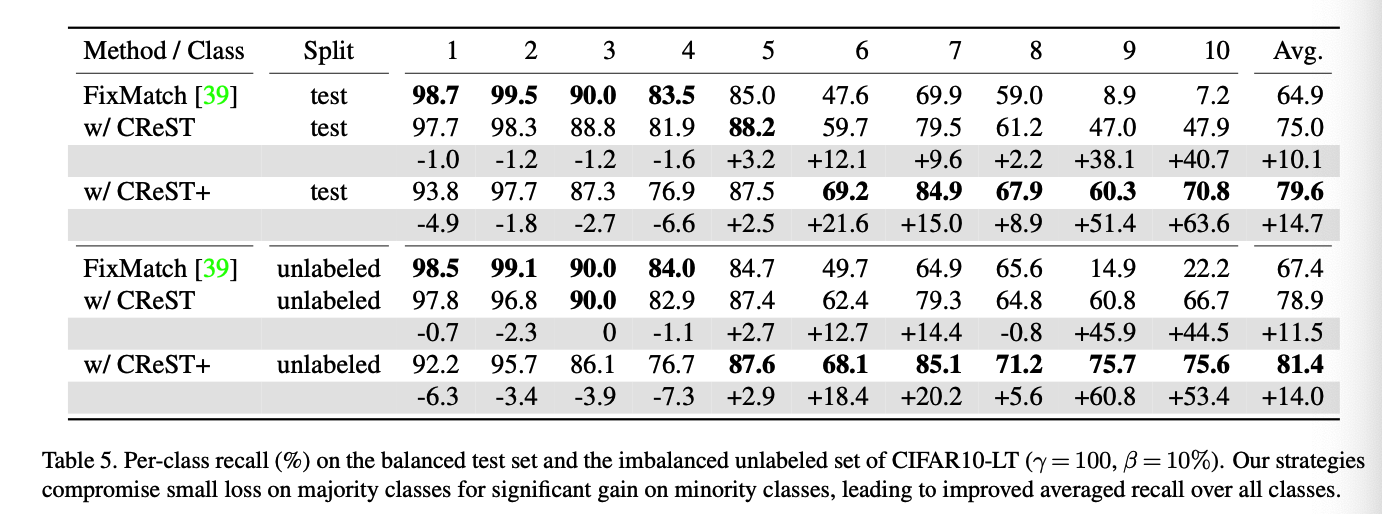
Undesired performance of existing Semi-SL algorithms on imbalanced data
\(\rightarrow\) Due to low recall on minority classes
( but note that …. precision on minority classes is surprisingly high !! )
- suggest that the model is conservative in classifying samples into minority classes, but once it makes such a prediction we can be confident it is correct.
Class-rebalancing self-training scheme (CReST)
-
re-trains a baseline Semi-SL model after adaptively sampling pseudo-labeled data from the unlabeled set
-
Generation = fully-trained baseline model
After each generation, pseudo-labeled samples from the unlabeled set are added into the labeled set to retrain an Semi-SL model.
-
CReST
- update labeled set with ALL pseudo-labeled samples (X)
- use a stochastic update strategy (O)
- samples are selected with higher probability if they are predicted as minority classes ( as those are more likely to be correct predictions )
-
Updating probability in CReST
- is a function of the data distribution estimated from the labeled set.
- extend CReST to CReST+ by incorporating distribution alignment with a temperature scaling factor
-
Figure 1-(c) & (d)
2. Related Work
(1) Semi-SL
Categories
-
a) Entropy minimization
-
b) Pseudo-labeling
-
c) Consistency regularization
b) Pseudo-labeling
- trains a classifier with unlabeled data using pseudo-labeled targets derived from the model’s own predictions
- use a model’s predictive probability with temperature scaling as a soft pseudo-label.
c) Consistency regularization
-
learns a classifier by promoting consistency in predictions between different views of unlabeled data
-
various effective methods of generating multiple views
Most recent Semi-SL methods relies on the quality of pseudo-labels
None of aforementioned works have studied Semi-SL in the class-imbalanced setting
- quality of pseudo-labels is significantly threatened by model bias !!
(2) Class-imbalanced supervised learning
a) Re-sampling & Re-weighting
- re-balance the contribution of each class
b) Transfer knowledge from majority classes to minority classes.
c) Decouple the learning of representation & classifier
\(\rightarrow\) Assume all labels are available during training ( not on Semi-SL setting )
(3) Class-imbalanced semi-supervised learning
( Semi-SL : Underexplored under class-imbalanced data. )
Yang and Xu
- leveraging unlabeled data by Semi-SL & SSL can benefit class-imbalanced learning.
Hyun et al.
- proposed a suppressed consistency loss to suppress the loss on minority classes.
Kim et al.
- proposed Distribution Aligning Refinery (DARP) to refine raw pseudo-labels via a convex optimization.
This paper : boost the quality of the model’s raw pseudo-labels directly via
- (1) Class-rebalancing sampling strategy
- (2) Progressive distribution alignment strategy
CReST vs. DARP
- DARP : setting where labeled and unlabeled data do not share the same class
- CReST : focus on the scenario when labeled and unlabeled data have roughly the same distribution.
3. Class-Imbalanced Semi-SL
(1) Problem setup and baselines
Class-imbalanced Semi-SL
-
\(L\)-class classification task
- Dataset : \(\mathcal{X}=\left\{\left(x_n, y_n\right): n \in(1, \ldots, N)\right\}\)
- \(x_n \in \mathbb{R}^d\).
- \(y_n \in\{1, \ldots, L\}\).
- \(N_l\) : Number of training examples in \(\mathcal{X}\) of class \(l\) ,
- \(\sum_{l=1}^L N_l=N\).
- \(N_1 \geq N_2 \geq \cdots \geq N_L\).
- The marginal class distribution of \(\mathcal{X}\) is skewed ( \(N_1 \gg N_L\). )
-
Imbalance ratio : \(\gamma=\frac{N_1}{N_L}\).
- Unlabeled set \(\mathcal{U}=\left\{u_m \in \mathbb{R}^d: m \in(1, \ldots, M)\right\}\)
- same class distribution as \(\mathcal{X}\)
- Label fraction \(\beta=\frac{N}{N+M}\) : percentage of labeled data.
Goal : Given class-imbalanced sets \(\mathcal{X}\) and \(\mathcal{U}\), learn a classifier \(f: \mathbb{R}^d \rightarrow\{1, \ldots, L\}\) that generalizes well under a class-balanced test criterion.
SOTA Semi-SL methods
- utilize unlabeled data by assigning a pseudo-label with the classifier’s prediction \(\hat{y}_m=f\left(u_m\right)\).
- then, useboth labeled and unlabeled samples to train classifier
When the classifier is biased at the beginning due to a skewed class distribution…
\(\rightarrow\) online pseudo-labels of unlabeled data can be even more biased!
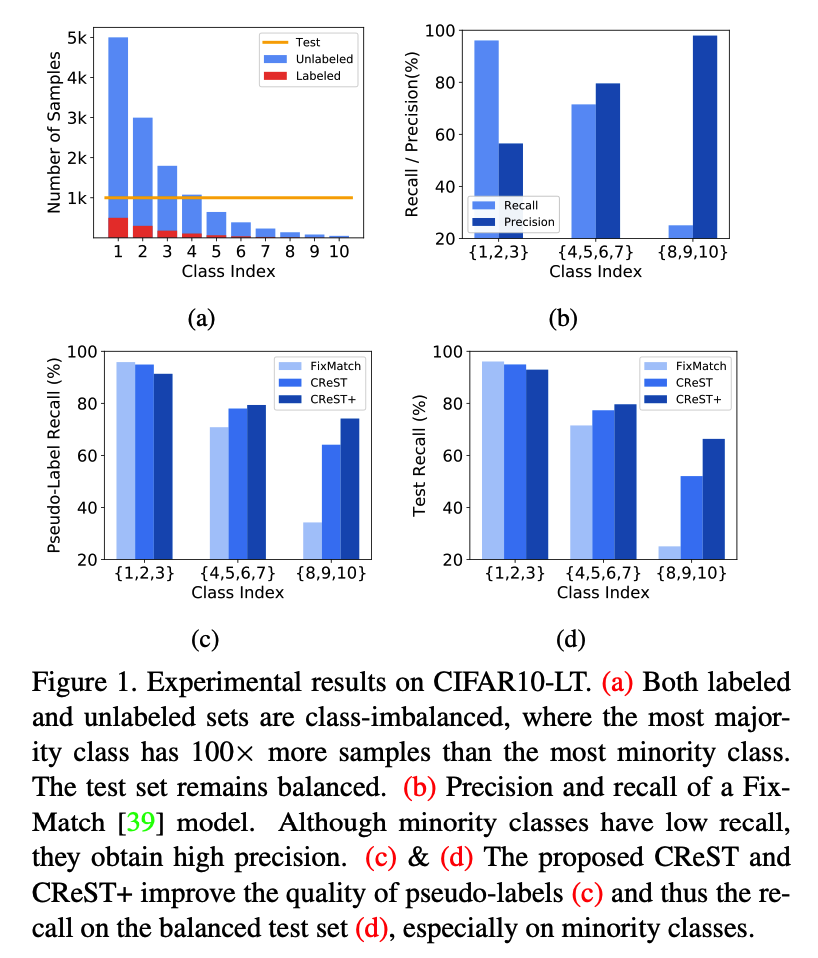
(2) A closer look at the model bias
Long-tailed versions of CIFAR
- with various class-imbalanced ratios
- to evaluate class-imbalanced fully-supervised learning algorithms.
This paper : follow the above protocol!
- some as LABELED
- some as UNLABELED
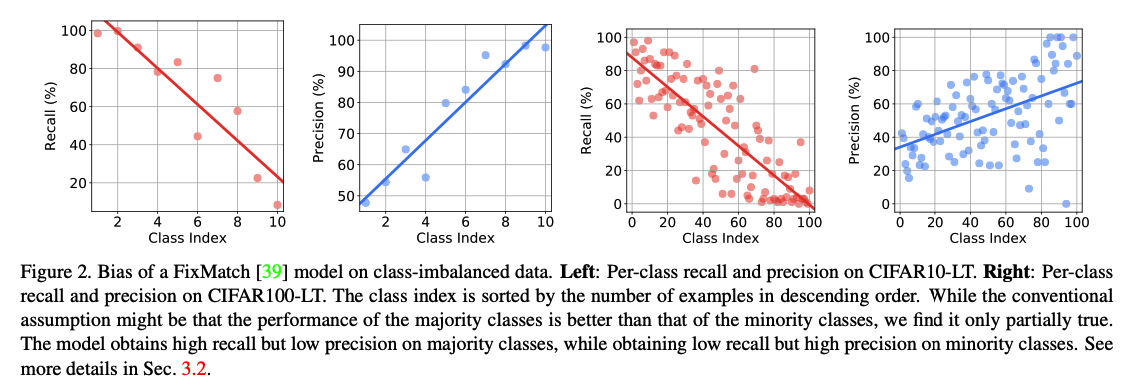
- Despite the low recall, the minority classes maintain surprisingly high precision!!!
(3) Class-rebalancing self-training
Self-training
- Iterative method widely used in Semi-SL.
- It trains the model for multiple generations, where each generation involves two steps.
- Procedure
- step 1) Trained on the labeled set to obtain a teacher model
- step 2) Teacher model’s predictions are used to generate pseudo-labels \(\hat{y}_m\) for unlabeled data \(u_m\).
- step 3) Add to labeled set for the next generation.
- \(\hat{\mathcal{U}}=\left\{\left(u_m, \hat{y}_m\right)\right\}_{m=1}^M\) .
- \(\mathcal{X}^{\prime}=\mathcal{X} \cup \hat{\mathcal{U}}\),
To accommodate the class-imbalance….
Propose two modifications to the self-training strategy!
(1) Instead of solely training on the labeled data, use Semi-SL algorithms to exploit both labeled and unlabeled data to get a better teacher model in the first step.
(2) Rather than including every sample in \(\hat{\mathcal{U}}\) in the labeled set, we instead expand the labeled set with a selected subset \(\hat{\mathcal{S}} \subset \hat{\mathcal{U}}\), i.e., \(\mathcal{X}^{\prime}=\mathcal{X} \cup \hat{\mathcal{S}}\).
- We choose \(\hat{\mathcal{S}}\) following a class-rebalancing rule:
- the less frequent a class \(l\) is, the more unlabeled samples that are predicted as class \(l\) are included into the pseudo-labeled set \(\hat{\mathcal{S}}\).
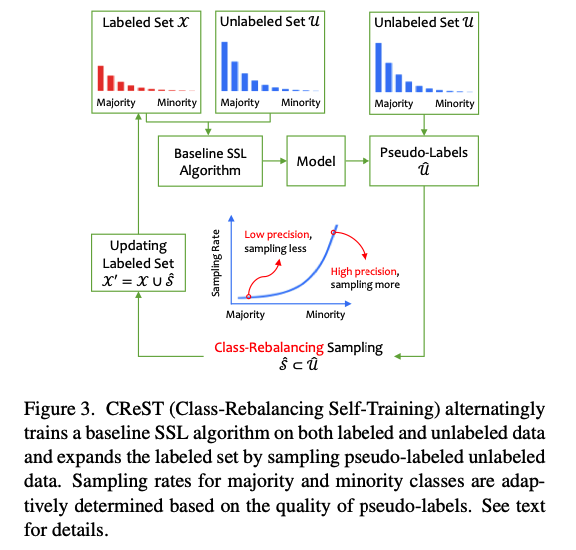
Class Distribution
- estimate from labeled set
- unlabeled samples that are predicted as class \(l\) are included into \(\hat{\mathcal{S}}\) at the rate of
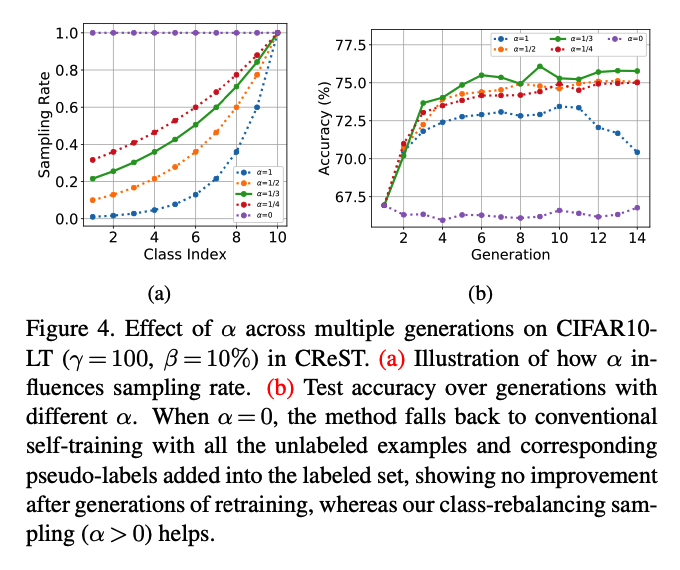
- \(\mu_l=\left(\frac{N_{L+1-l}}{N_1}\right)^\alpha\).
- \(\alpha \geq 0\) : tunes the sampling rate
- \(\mu_l=\left(\frac{N_{L+1-l}}{N_1}\right)^\alpha\).
- Ex) 10-class imbalanced dataset with imbalance ratio of \(\gamma=\frac{N_1}{N_{10}}=100\),
- samples predicted as the most minority class
- keep all ! … \(\mu_{10}=\left(\frac{N_{10+1-10}}{N_1}\right)^\alpha=1\).
- samples predicted as the most majority class
- Only \(\mu_1=\left(\frac{N_{10+1-1}}{N_1}\right)^\alpha=0.01^\alpha\) of samples are selected.
- samples predicted as the most minority class
- When \(\alpha=0, \mu_l=1\) for all \(l\), then all unlabeled samples are kept and the algorithm falls back to the conventional self-training.
When selecting pseudo-labeled samples in each class, we take the most confident ones.
Motivation of our CReST strategy
- Precision of minority classes is much higher than that of majority classes
- minority class pseudo-labels are less risky to include in the labeled set.
- Adding samples to minority classes is more critical due to data scarcity.
(4) Progressive Distribution Alignment
Improve the quality of online pseudo-labels …
by additionally introducing progressive distribution alignment into CReST
=> CReST +
Distribution Alignment (DA)
-
introduced for class-balanced Semi-SL
( also fits with also for class-imbalanced ! )
-
aligns the model’s predictive distribution ( on unlabeled samples )
with the labeled training set’s class distribution \(p(y)\).
\(\tilde{p}(y)\) : MA of the model’s predictions on unlabeled examples.
Procedure of DA
-
Step 1) Scales the model’s prediction \(q=p\left(y \mid u_m ; f\right)\) for an unlabeled example \(u_m\) by the ratio \(\frac{p(y)}{\tilde{p}(y)}\)
( = aligning \(q\) with the target distribution \(p(y)\). )
-
Step 2) Re-normalizes the scaled result
- \(\tilde{q}=\operatorname{Normalize}\left(q \frac{p(y)}{\tilde{p}(y)}\right)\), where Normalize \((x)_i=x_i / \sum_j x_j\).
- use \(\tilde{q}\) instead of \(q\) for the label guess for \(u_m\)
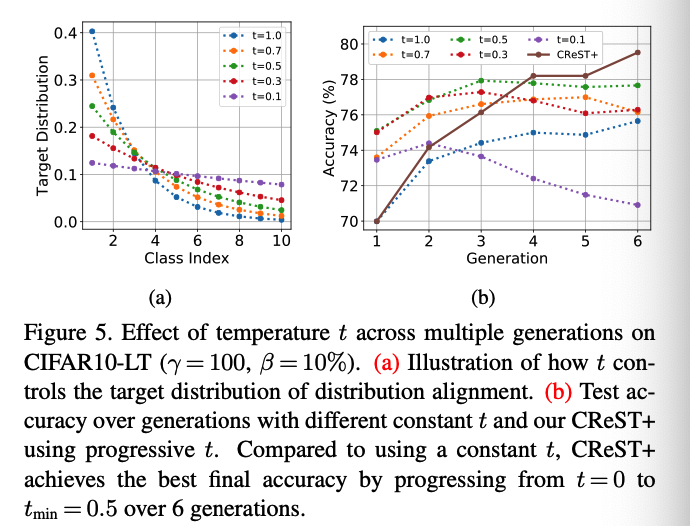
Progressive DA
- use temperature scaling to enhance DA’s ability to handle class-imbalanced data
- add a tuning knob \(t \in[0,1]\)
- controls the class-rebalancing strength of DA.
- Use \(\operatorname{Normalize}\left(p(y)^t\right)\) instead of \(p(y)\) as target,
- When \(t=1\), same as original DA
- When \(t<1\), the taget distn becomes smoother and balances the model’s predictive distribution more aggressively.
- When \(t=0\), the target distribution becomes uniforrm
Pogressively increase the strength of class-rebalancing by decreasing \(t\) over generations.
- \(t_g=\left(1-\frac{g}{G}\right) \cdot 1.0+\frac{g}{G} \cdot t_{\min }\).
- \(G+1\) : total number of generations
- \(t_{\min }\) : temperature used for the last generation
- Enjoys both
- high precision of pseudo-labels in early generations
- stronger class-rebalancing in late generations.
4. Experiments
(1) CIFAR-LT
Datasets
- CIFAR10-LT
- CIFAR100-LT
Training images
- randomly discarded per class
- pre-defined imbalance ratio \(\gamma\).
- \(N_l=\gamma^{-\frac{l-1}{L-1}} \cdot N_1\) .
- (CIFAR10-LT) \(N_1=5000, L=10\)
- (CIFAR100-LT) \(N_1=500, L=100\)
Experimental Settings
- (1) Unlabeled ratio : \(\beta\)
- Randomly select \(\beta=10 \%\) and \(30 \%\) of samples from training data as labeled set
- (2) Imbalance ratio : \(\gamma\)
- (CIFAR10-LT) \(\gamma\) = 50, 100, 200
- (CIFAR100-LT) \(\gamma\) = 50, 100
Testing images
- remains untouched
- balanced ( thus evaluated criterion is on class-balanced dataset )
a) Main Results
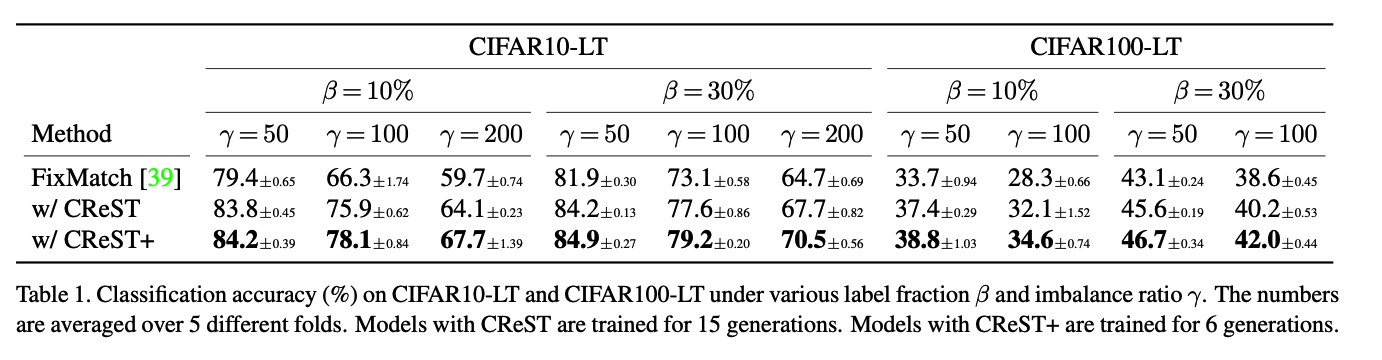
b) Comparison with baselines
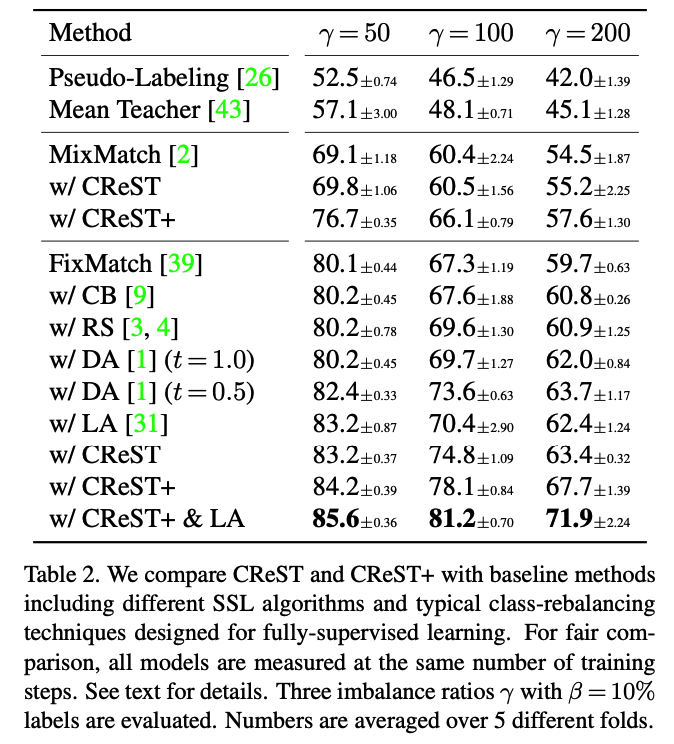
c) Comparison with DARP
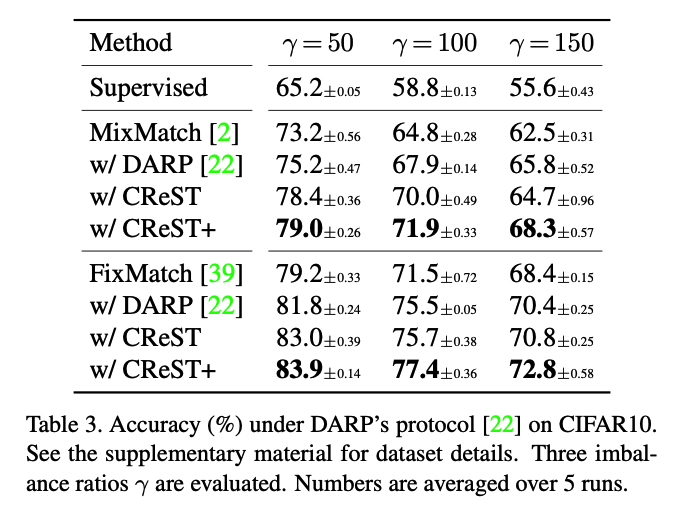
(2) ImageNet127
Dataset
-
Large-scale datasets.
- 1000 classes of ImageNet \(\rightarrow\) Grouped into 127 classes
- based on their top-down hierarchy in WordNet.
-
Imbalanced dataset
-
with imbalance ratio \(\gamma=286\).
- Majority Class : “mammal”
- consists of 218 original classes
- 277,601 training images.
- Minority Class : “butterfly”
- single original class
- 969 training examples.
-
Experimental Settings
-
Randomly select \(\beta=10 \%\) training samples as the labeled set
-
Due to class grouping, the test set is not balanced.
\(\rightarrow\) Compute averaged class recall ( instead of accuracy ) for balanced metric
iNaturalist, ImageNet-LT ( other large-scale datasets )
- serve as testbeds for fully-supervised long-tailed recognition algorithms.
- But contain TOO FEW examples of minority classes to form a statistically meaningful dataset and draw reliable conclusions for semi-supervised learning.
- ex) only 5 examples in the most minority class of the ImageNet-LT dataset.
Setup
- bacbkone : ResNet50
- hyperparameters : adopted from the original FixMatch
- Self-trained for 3 generations with \(\alpha=0.7\) and \(t_{\min }=0.5\).
a) Results
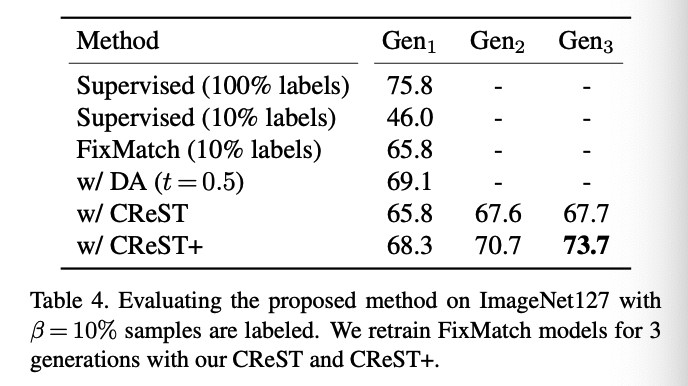
(3) Ablation Study
a) Effect of sampling rate
b) Effect of progrerssive temperature scaling
c) Per-class performance