(paper) A DIRT-T Approach to Unsupervised Domain Adaptation

A DIRT-T Approach to Unsupervised Domain Adaptation ( 2018, 380 )

Contents

1. Abstract
2. Introduction
3. Limitation of Domain Adversarial Training
4. Constraining via “Conditional Entropy Minimization”
5. Decision Boundary Iterative Refinement Training (DIRT)
6. Summary

0. Abstract

Domain Adaptation

• leveraging “labeled data” in source domain
• to learn an accurate model for “TARGET domain” ( where labels are scarce )

Domain Adversarial Training

induce “feature extractor”…

• that matches the “source & target feature” distributions in some feature space

2 Limitations

• 1) if feature extractor has “high capacity”

  \(\rightarrow\) feature disn matching is a weak constraint

• 2) in “non-conservative DA”

  ( = NO single classifier works well for both domain )

  \(\rightarrow\) training the to “do well on source domain” hurts performance on target domain

propose 2 models

• 1) VADA ( Virtual Adversarial Domain Adaptation )
• 2) DIRT-T ( Decision-boundary Iterative Refinement Training with a Teacher)

1. Introduction

consider a challenging setting… “non-conservative DA”

non-conservative DA

• 1) provided with…
  • “fully-labeled SOURCE data”
  • “completely-unlabeled TARGET data”
• 2) existence of classifier with LOW ERROR on BOTH DOMAIN is not guaranteed

( \(\leftrightarrow\) existence of classifier that works well on both )

Previous works

Ganin & Lempitsky (2015)

• constrain the classifier, to rely on “domain-invariant features”
• employ “domain adversarial training”

\(\rightarrow\) tackle the 2 problems of this ( in Abstract )

Saito et al (2017)

• replace “domain adversarial training” with asymmetric tri-training(ATT)
  • assumption : target samples, labeled by source-classifier with HIGH confidence, are “correctly labeled”

This paper

• consider an orthogonal assumption, “CLUSTER ASSUMPTION”
  • input distribution = separated data clusters
    • data in data cluster = share same class label
• based on this assumption, propose..
  • 1) VADA ( Virtual Adversarial DA )
    • VADA = (1) “additional virtual adversarial training” + (2) “conditional entropy loss”
  • 2) DIRT-T ( Decision-boundary Iterative Refinement Training with a Teacher )
    • use natural gradients to further refine the output of VADA
    • focus purely on “target domain”

VADA & DIRT-T

[ conservative DA ]

• classifier is trained to perform well on “SOURCE” domain

• use VADA to “further constrain” the hypothesis space,

  by penalizing violations of the cluster assumption

[ non-conservative DA ]

• mismatch between source & target optimal classifiers
• use DIRT-T to transit from joint classifier \(\rightarrow\) better “TARGET” domain classifier

2. Limitation of Domain Adversarial Training

“Domain Adversarial Training is NOT SUFFICIENT”

• especially, when “feature extractor has HIGH capacity”

Classifier ( \(h=g \circ f\) )

• 1) embedding function : \(f_{\theta}: \mathcal{X} \rightarrow \mathcal{Z}\)
• 2) embedding classifier : \(g_{\theta}: \mathcal{Z} \rightarrow \mathcal{C}\)

Notation

• ( source domain ) \(\mathcal{D}_{s}\): joint distn over input \(x\) & one-hot label \(y\)
  • \(X_{s}\) : marginal input distribution
• ( target domain ) \(\left(\mathcal{D}_{t}, X_{t}\right)\) : ~
• \(\left(\mathcal{L}_{s}, \mathcal{L}_{d}\right)\) : loss function

Loss Function

• (1) cross-entropy objective
  • \(\mathcal{L}_{y}\left(\theta ; \mathcal{D}_{s}\right) =\mathbb{E}_{x, y \sim \mathcal{D}_{s}}\left[y^{\top} \ln h_{\theta}(x)\right]\) .
• (2) domain discriminator (\(D\)) loss
  • \(\mathcal{L}_{d}\left(\theta ; \mathcal{D}_{s}, \mathcal{D}_{t}\right) =\sup _{D} \mathbb{E}_{x \sim \mathcal{D}_{s}}\left[\ln D\left(f_{\theta}(x)\right)\right]+\mathbb{E}_{x \sim \mathcal{D}_{t}}\left[\ln \left(1-D\left(f_{\theta}(x)\right)\right)\right]\).

\(\rightarrow\) Total loss : \(\min _{\theta} \mathcal{L}_{y}\left(\theta ; \mathcal{D}_{s}\right)+\lambda_{d} \mathcal{L}_{d}\left(\theta ; \mathcal{D}_{s}, \mathcal{D}_{t}\right)\)

but what if \(f\) is toooo flexible??

\(\rightarrow\) does not imply high accuracy on “target task”

3. Constraining via “Conditional Entropy Minimization”

Cluster Assumption

• input distn \(X\) contains clusters
• points inside same cluster come from same class

If this assumption holds, optimal decision boundaries should occur FAR AWAY from data-dense regions

\(\rightarrow\) achieve this by “minimization of CONDITIONAL ENTROPY, w.r.t target distribution”

( = force the classifier to be confident on target data )

• \(\mathcal{L}_{c}\left(\theta ; \mathcal{D}_{t}\right)=-\mathbb{E}_{x \sim \mathcal{D}_{t}}\left[h_{\theta}(x)^{\top} \ln h_{\theta}(x)\right]\).

How to estimate conditional entropy?

• must be “empirically estimated” using available data

• but…this approximation breaks down, “if classifier \(h\) is not locally-Licpschitz”

  • thus, add additional term to loss function :

    \(\mathcal{L}_{v}(\theta ; \mathcal{D})=\mathbb{E}_{x \sim \mathcal{D}}\left[\max _{ \mid \mid r \mid \mid \leq \epsilon} \mathrm{D}_{\mathrm{KL}}\left(h_{\theta}(x) \mid \mid h_{\theta}(x+r)\right)\right]\).

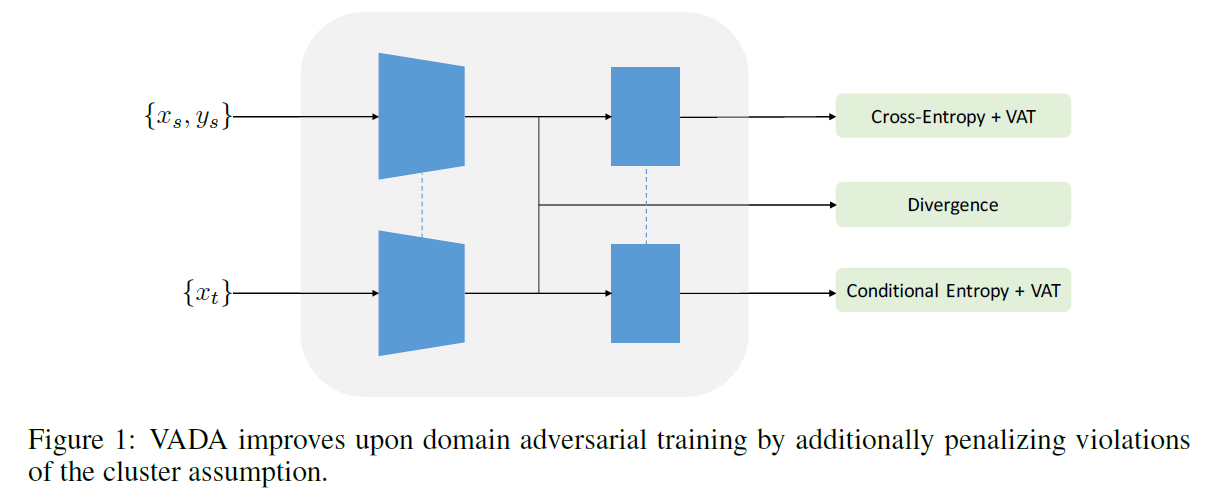
Final Loss Function ( of VADA )

• \(\min _{\theta} \mathcal{L}_{y}\left(\theta ; \mathcal{D}_{s}\right)+\lambda_{d} \mathcal{L}_{d}\left(\theta ; \mathcal{D}_{s}, \mathcal{D}_{t}\right)+\lambda_{s} \mathcal{L}_{v}\left(\theta ; \mathcal{D}_{s}\right)+\lambda_{t}\left[\mathcal{L}_{v}\left(\theta ; \mathcal{D}_{t}\right)+\mathcal{L}_{c}\left(\theta ; \mathcal{D}_{t}\right)\right]\).
  • 1) \(\mathcal{L}_{y}\left(\theta ; \mathcal{D}_{s}\right)\) : CE loss
  • 2) \(\mathcal{L}_{d}\left(\theta ; \mathcal{D}_{s}, \mathcal{D}_{t}\right)\) : domain discriminator loss
  • 3) \(\mathcal{L}_{v}\left(\theta ; \mathcal{D}_{s}\right)\) : term for “locally-Lipschitz” ( for SOURCE )
  • 4) \(\mathcal{L}_{v}\left(\theta ; \mathcal{D}_{t}\right)+\mathcal{L}_{c}\left(\theta ; \mathcal{D}_{t}\right)\) : term for “locally-Lipschitz” & “conditional entropy” ( for TARGET )

4. Decision Boundary Iterative Refinement Training (DIRT)

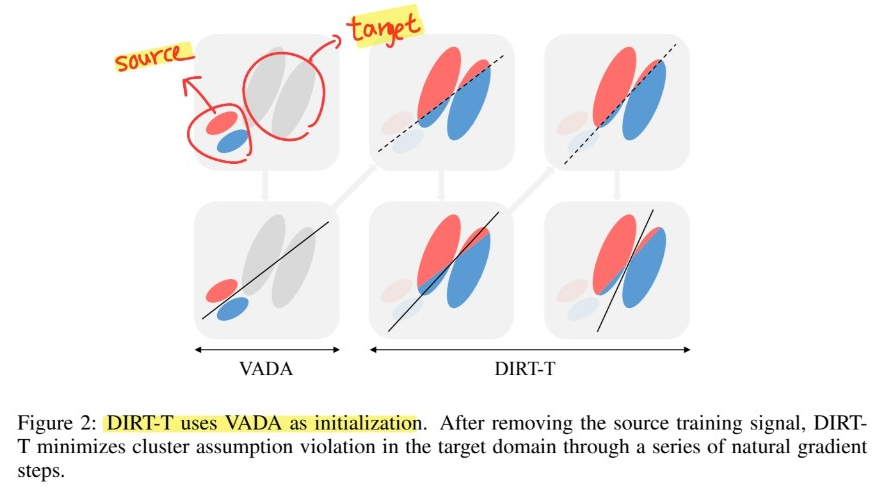
Optimal classifier in source domain, does not coincide with the optimal classifier in target domain

Any source-optimal classifier drawn from our hypothesis space necessarily violates the cluster assumption in target domain

Solution

• step 1) (Initialization)

  • initialize with VADA model

• step 2) (Refinement)

  • minimize the cluster assumption violation in target domain

  • incrementally push the classifier’s decision boundaries, away from data-dense regions,

    by minimizing the target-side cluster assumption violation loss \(\mathcal{L}_t\)

  • \(\mathcal{L}_{t}(\theta)=\mathcal{L}_{v}\left(\theta ; \mathcal{D}_{t}\right)+\mathcal{L}_{c}\left(\theta ; D_{t}\right)\).

5. Summary

DIRT-T = recursive extension of VADA

• act of pseudo-labeling of the target distribution constructs a new SOURCE domain