Maximum Classifier Discrepancy for Unsupervised Domain Adaptation ( 2017, 949 )
Contents
- Abstract
0. Abstract
2 problems in (previous) DA methods
-
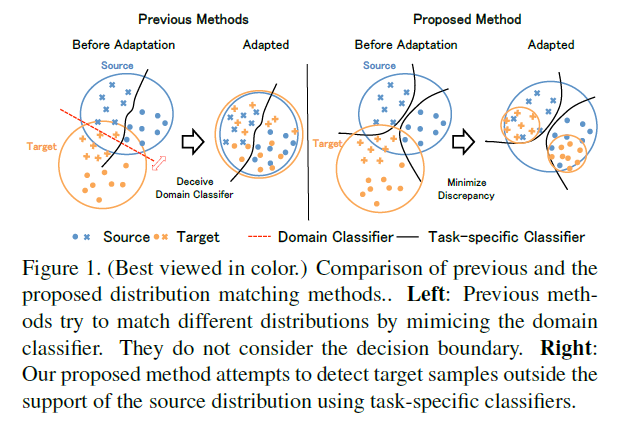
1) domain classifier only tries to distinguish S&T,
and does not consider “task-specific” decision boundaries between classes
-
2) these methods aim to completely match the feature distn between domains,
which is difficult due to each domain’s characteristics
Proposal
-
align distributions of S&T by utilizing the “task specific decision boundaries”
-
maximize the “discrepancy” between 2 classifier’s outputs
to detect target samples that are far from the support of the source
1. Introduction
-
each domains’ samples : have different characteristics
-
propose a method for UDA (Unsupervised DA)
Lots of UDA algorithsm…
- 1) do not consider “the category of the samples”
- 2) in adversarial manner
- domain classifier ( = discriminator ) & feature generator
\(\rightarrow\) fail to extract “discriminative features”
To overcome these problems…
\(\rightarrow\) propose to “align distributions of features from S & T”,
by using the “classifier’s output for T”
Proposal : 2 types of players…
-
1) task-specific classifier : do both a) & b)
- a) try to classify source sample correctly
- b) trained to detect target samples far from support
-
2) feature generator
-
tries to fool classifier
( = generate T features “near the support” , while considering classifier’s output for T )
-
2. Method
(1) Overall Idea
Dataset
- [source] \(\left\{X_{s}, Y_{s}\right\}\)
- [target]\(X_{t}\)
Model
-
feature generator : \(G\)
-
classifier : \(F_1\) & \(F_2\)
-
classify them to \(K\) classes
( output a \(K\)-dim vector of logits )
-
output : \(p_{1}(\mathbf{y} \mid \mathbf{x}), p_{2}(\mathbf{y} \mid \mathbf{x})\)
-
Goal : align source & target features,
- by utilizing the task-specific classifiers as a discriminator,
- in order to consider the “relationship between class boundaries & target samples”
\(\rightarrow\) have to detect target samples FAR from the support of the source
propose to utilize the disagreement of 2 classifiers, on the prediction for target samples
( assume 2 classifiers classify well on source domain )
- discrepancy : \(d\left(p_{1}\left(\mathbf{y} \mid \mathbf{x}_{\mathbf{t}}\right), p_{2}\left(\mathbf{y} \mid \mathbf{x}_{\mathbf{t}}\right)\right)\).
- generator : MINIMIZE
- classifier : MAXIMIZE
(2) Discrepancy Loss
define it as “difference between 2 classifier’s probabilistic output”
- \(d\left(p_{1}, p_{2}\right)=\frac{1}{K} \sum_{k=1}^{K}\mid p_{1_{k}}-p_{2_{k}}\mid\).
- \(p_{1k}\) : probability output of \(p_q\) for class \(k\)
(3) Training Steps
Need to train…
- 1) Two task-specific classifiers…. maximize \(d\left(p_{1}\left(\mathbf{y} \mid \mathbf{x}_{\mathbf{t}}\right), p_{2}\left(\mathbf{y} \mid \mathbf{x}_{\mathbf{t}}\right)\right)\)
- 2) One generator ….. minimize \(d\left(p_{1}\left(\mathbf{y} \mid \mathbf{x}_{\mathbf{t}}\right), p_{2}\left(\mathbf{y} \mid \mathbf{x}_{\mathbf{t}}\right)\right)\)
Step 1) train both
minimize softmax CE loss :
-
\(\min _{G, F_{1}, F_{2}} \mathcal{L}\left(X_{s}, Y_{s}\right)\),
where \(\mathcal{L}\left(X_{s}, Y_{s}\right)=-\mathbb{E}_{\left(\mathbf{x}_{\mathbf{s}}, y_{s}\right) \sim\left(X_{s}, Y_{s}\right)} \sum_{k=1}^{K} \mathbb{1}_{\left[k=y_{s}\right]} \log p\left(\mathbf{y} \mid \mathbf{x}_{s}\right)\).
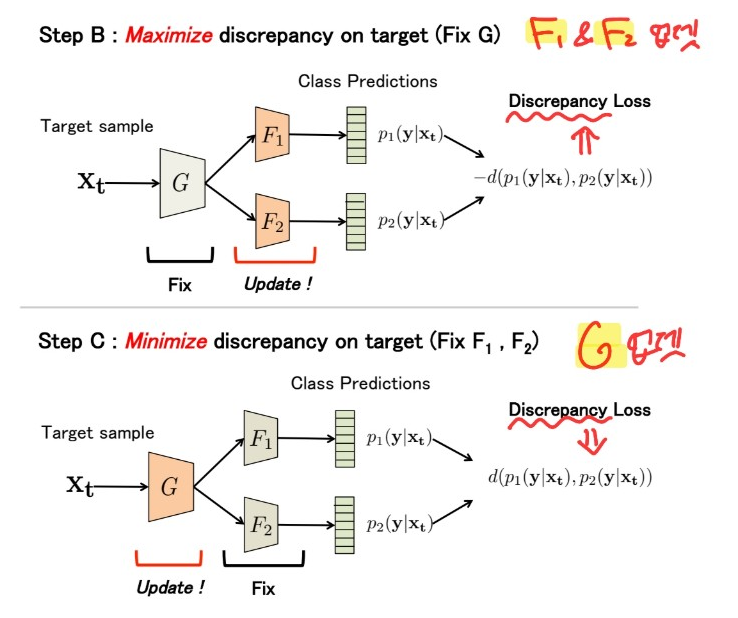
Step 2) train \(F_1\) &\(F_2\)
have to maximize discrepancy
-
\(\min _{F_{1}, F_{2}} \mathcal{L}\left(X_{s}, Y_{s}\right)-\mathcal{L}_{\mathrm{adv}}\left(X_{t}\right)\),
where \(\begin{gathered} \mathcal{L}_{\mathrm{adv}}\left(X_{t}\right)=\mathbb{E}_{\mathbf{x}_{\mathbf{t}} \sim X_{t}}\left[d\left(p_{1}\left(\mathbf{y} \mid \mathbf{x}_{\mathbf{t}}\right), p_{2}\left(\mathbf{y} \mid \mathbf{x}_{\mathbf{t}}\right)\right)\right] \end{gathered}\)
Step 3) train \(G\)
have to minimize discrepancy
- \(\min _{G} \mathcal{L}_{\mathrm{adv}}\left(X_{t}\right)\).