2.Distributed Representations of Words and Phrases and their Compositionality (2013)
목차
-
Abstract
-
Introduction
-
Skip-gram model
- Hierarchical Softmax
- Negative Sampling
- Subsampling of Frequent words
Abstract
Skip-gram model :
-
(1) “efficient” method for learning (2) “distributed vector representation”
-
Not only just the co-occurence of the word
But also captures its meaning!
This paper suggests extensions that improves both
- 1) “quality of the vectors”
- 2) “training speed”
How? By..
- 1) SUBSAMPLING of frequent words
- 2) NEGATIVE SAMPLING ( alternative to hierarchical softmax )
Limitation of word representation?
- 1) indifference to word order
- 2) inability to represent idiomatic phrases
- ex) airport “Air Canada” \(\neq\) Air + Canada
1. Introduction
Distributed respresentation of words, using Skip-gram Model
Skip-gram model
- Efficient estimation of word representations in vector space. (Mikolov et al, 2013)
- unlike NN, no dense matrix multiplication \(\rightarrow\) efficient
- can encode its meaning!
- ex) King - Man + Woman = Queen
This paper introduces extension of original Skip-gram model.
- 1) Subsampling of frequent words
- speed up (2x ~ 10x)
- improves accuracy of less frequent words
-
2) variant of NCE (Noise Contrastive Estimation)
- faster training
- better vector representations
( compared to Hierarchical Softmax )
Limitation of word representations : “Inability to represent idiomatic phrases”
- ex) airport “Air Canada” \(\neq\) Air + Canada
-
using vectors to represent the “whole phrase” ( “Air Canada” as one phrase )
- How to extend from “word-based” to “phrase-based” model? SIMPLE!
- 1) identify a large number of phrases
- 2) treat the phrases as individual tokens
2. The Skip-gram Model
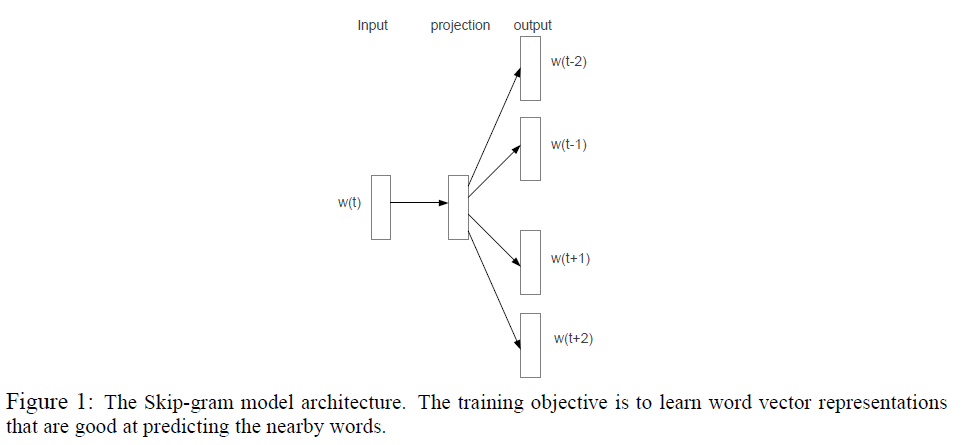
CBOW vs Skip-gram
-
CBOW : predicting the current word based on the context
-
Skip-gram : predicting words within a certain range before and after the current word, given current word.
Training Skip-gram
-
How? “Maximize the average log probability”
\(\frac{1}{T} \sum_{t=1}^{T} \sum_{-c \leq j \leq c, j \neq 0} \log p\left(w_{t+j} \mid w_{t}\right)\).
- \(c\) : size of the training context
- Larger \(c\) ( = more training examples ) \(\rightarrow\) higher accuracy, slower speed
-
softmax function
\(p\left(w_{O} \mid w_{I}\right)=\frac{\exp \left(v_{w_{O}}^{\prime}{ }^{\top} v_{w_{I}}\right)}{\sum_{w=1}^{W} \exp \left(v_{w}^{\prime}{ }^{\top} v_{w_{I}}\right)}\).
- \(v_w\) : input
- \(v_w'\) : output
- \(W\) : number of words (vocab)
\(\rightarrow\) Impractical ! Too many words! ( \(10^5 \sim 1-^7\) terms)
\(\nabla \log p\left(w_{O} \mid w_{I}\right)\) is proportional to \(W\)
Inefficient of using all the \(W\) words?
-
softmax function : \(\hat{y}_{i}=P(i \mid c)=\frac{\exp \left(u_{i}^{T} v_{c}\right)}{\sum_{w=1}^{W} \exp \left(u_{w}^{T} v_{c}\right)}\).
where \(u_i\) and \(v_j\) are the column vectors of embedded matrix
( let \(U=\left[u_{1}, u_{2}, \ldots, u_{k}, \ldots u_{W}\right]\) be a matrix composed of \(u_{k}\) column vectors )
-
loss : Cross Entropy Loss : \(J=-\sum_{i=1}^{W} y_{i} \log \left(\hat{y}_{i}\right)\).
where \(y\) : one-hot encoded vector & \(\hat{y}\) : softmax prediction
\(\begin{aligned}J&=-\sum_{i=1}^{W} y_{i} \log \left(\frac{\exp \left(u_{i}^{T} v_{c}\right)}{\sum_{w=1}^{W} \exp \left(u_{w}^{T} v_{c}\right)}\right)\\ &=-\sum_{i=1}^{W} y_{i}\left[u_{i}^{T} v_{c}-\log \left(\sum_{w=1}^{W} \exp \left(u_{w}^{T} v_{c}\right)\right)\right]\\ &=-y_{k}\left[u_{k}^{T} v_{c}-\log \left(\sum_{w=1}^{W} \exp \left(u_{w}^{T} v_{c}\right)\right)\right]\end{aligned}\).
Thus…
\(\begin{aligned}\frac{\partial J}{\partial v_{c}}&=-\left[u_{k}-\frac{\sum_{w=1}^{W} \exp \left(u_{w}^{T} v_{c}\right) u_{w}}{\sum_{x=1}^{W} \exp \left(u_{x}^{T} v_{c}\right)}\right]\\ &=\sum_{w=1}^{W}\left(\frac{\exp \left(u_{w}^{T} v_{c}\right)}{\sum_{x=1}^{W} \exp \left(u_{x}^{T} v_{c}\right)} u_{w}\right)-u_{k}\\ &=\sum_{w=1}^{W}\left(\hat{y}_{w} u_{w}\right)-u_{k}\end{aligned}\).
How to solve this?
- 1) Hierarchical Softmax
- 2) Negative Sampling
2-1. Hierarchical Softmax
( details : refer to https://seunghan96.github.io/ne/03.Hierarchical_Softmax/ )
Key points
- uses binary tree representation
- instead of evaluating \(W\) output nodes, only need to evaluate \(\log_2(W)\) nodes
- define a random walk that assings probabilities to words
2-2. Negative Sampling
( details : refer to https://seunghan96.github.io/ne/04.Negative_Sampling/ )
Key points
-
alternative to hierarchical softmax : NCE (Noise Contrastive Estimation)
- good model = able to differentiat data from noise, using log reg
- simplified NCE = Negative Sampling
-
Negative sampling : use \(k\) negative samples ( = wrong answers )
-
(Standard) Objective function
\(p\left(w_{O} \mid w_{I}\right)=\frac{\exp \left(v_{w_{O}}^{\prime}{ }^{\top} v_{w_{I}}\right)}{\sum_{w=1}^{W} \exp \left(v_{w}^{\prime}{ }^{\top} v_{w_{I}}\right)}\).
\(\log p\left(w_{O} \mid w_{I}\right)=\left(v_{w_{O}}^{\prime}{ }^{\top} v_{w_{I}}\right) - \log \sum_{w=1}^{W} \exp \left(v_{w}^{\prime}{ }^{\top} v_{w_{I}}\right)\).
-
(Proposed) instead of \(\log p\left(w_{O} \mid w_{I}\right)\)…
\(\log \sigma\left(v_{w_{O}}^{\prime}{ }^{\top} v_{w_{I}}\right)+\sum_{i=1}^{k} \mathbb{E}_{w_{i} \sim P_{n}(w)}\left[\log \sigma\left(-v_{w_{i}}^{\prime}{ }^{\top} v_{w_{I}}\right)\right]\).
-
Distinguish target word \(w_O\) from draws from the noise distn \(P_n(w)\) ,
using logistic regression (sigmoid func)
2-3. Subsampling of Frequent Words
most frequent words : occur hundreds of millions of times!
do not give even probability of getting sampled!
-
More Frequently occured, Less Probability of getting sampled
-
\(P\left(w_{i}\right)=1-\sqrt{\frac{t}{f\left(w_{i}\right)}}\).
where \(f(w_i)\) : frequency of word \(i\) & \(t\) : chosen threshold
