WGAN (Wasserstein GAN)

WGAN (Wasserstein GAN)

1. Introduction

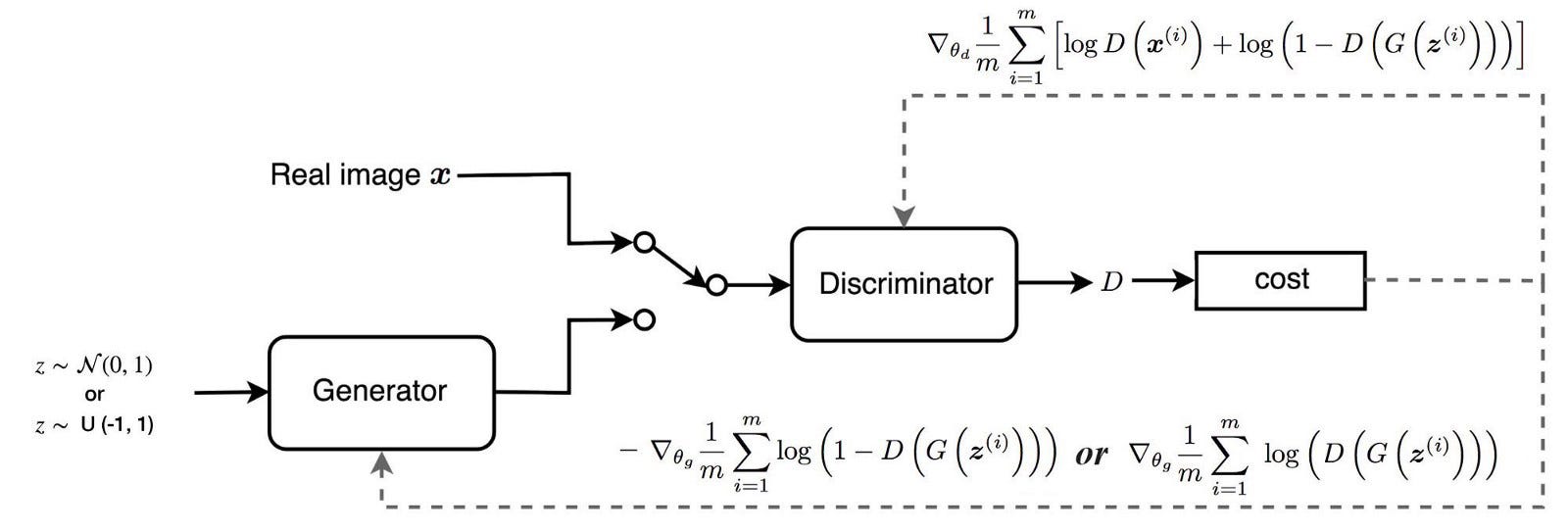
지금까지 봐왔던 GAN (GAN & CGAN)은 훈련하기 어렵고, mode collapse될 가능성이 있다. Mode collapse란, Loss Function을 minimize하여 이미 최적화가 되었음에도 불구하고, 계속 똑같은 output만을 출력하는 경우를 말한다. 이를 해결하기 위한 방법 중 하나가 WGAN이다. WGAN은 Loss Function으로 Wasserstein Distance를 사용한다.

https://miro.medium.com/max/3200/1*M_YipQF_oC6owsU1VVrfhg.jpeg

2. Various Distance

GAN을 훈련시키기 위해, 우리는 Generator가 만들어낸 가짜 정답과 진짜 정답, 이 둘 간의 차이를 최소화한다. 여기서 즉, 우리는 Generator가 만들어낸 가짜 데이터의 분포\(p_g\)를 진짜 데이터의 분포인 \(p_{data}\)와 유사하게 만들기 위해, 이 두 분포간의 거리를 minimize한다. 여기서 ‘거리’를 어떻게 정의하냐에 따라 GAN의 성능은 달라진다.

두 분포 사이의 거리를 나타내는 대표적인 지표로는 다음과 같이 3가지가 있다.

( 엄밀히 말하면, (1)KL-Divergence는 ‘거리’라고 할 수 없다. 거리는 symmetric해야 하지만, KL-Divergence는 해당 조건을 충족시키지 못한다. 하지만 두 분포 사이의 차이를 나타낸다는 점에서 여기서 함께 설명하겠다 )

(1) KL Divergence ( Kullback-Leibler Divergence)

\[D_{KL} (p_{data} \mid\mid p_{g} ) = E_{x \sim p_{data}}log\frac{p_{data}(x)}{p_{g}(x)}\]

• symmetric하지 않다 ( \(D_{KL} (p_{data} \mid\mid p_{g} )\) \(\neq\) \(D_{KL} (p_{g} \mid\mid p_{data} )\))

(2) JS Divergence ( Jensen-Shannon Divergence)

\[D_{JS} (p_{data} \mid\mid p_{g} ) = \frac{1}{2}E_{x \sim p_{data}}log\frac{p_{data}(x)}{\frac{p_{data}(x) + p_{g}(x)}{2}} + \frac{1}{2}E_{x \sim p_{g}}log\frac{p_{g}(x)}{\frac{p_{data}(x) + p_{g}(x)}{2}}\]

(3) EMD ( Earth-Mover Distance )

• also called “Wesserstein Distance”

\[W(p_{data},p_g) = \underset{\gamma \in \prod (p_{data},p_g)}{inf}E_{(x,y)\sim \gamma}[\mid\mid x-y \mid\mid]\]

여기서 (3) EMD를 직관적으로 해석하자면, 이는 분포 \(p_{data}\) 를 분포 \(p_{g}\)와 같게 만들기 위해 “얼마나 많은 질량”을 “얼만큼의 거리”를 움직여야하는가?를 의미한다.

• 얼마나 많은 질량 : \(\gamma (x,y)\)
• 얼만큼의 거리 : \(d = \mid\mid x-y\mid\mid\)

3. Loss Function of WGAN

우리는 이전 포스트에서 GAN의 Discriminator의 Loss function이 다음과 같음을 확인했었다.

\(L^{(D)}\) = \(-E_{x \sim P_{data}}logD(x)\) \(-E_{z}log(1-D(G(z)))\)

위 식에서 \(z\) (노이즈)에서 샘플링 하는 대신, Generator의 분포에서 샘플링을하면 위 식을 다음과 같이 표현할 수 있다.

\(L^{(D)}\) = \(-E_{x \sim P_{data}}logD(x)\) \(-E_{p_g}log(1-D(x))\)

위 식을 정리하면 다음과 같다.

\[L^{(D)} = - \int_{x} p_{data}(x) logD(x)dx - \int_{x}p_g(x)log(1-D(x))dx\] \[= -\int _{x} (p_{data}logD(x) + p_g(x)log(1-D(x)))dx\]

이 식을 D(x)에 관해 미분하여 최적의 Discriminator를 구하면, 다음과 같이 나오게 된다.

\[D^*(x) = \frac{p_{data}}{p_{data} + p_g}\]

이것을 대입하고 정리하면 다음과 같이 나온다.

\[\begin{align*} L^{(D^{*})} &= - E_{x \sim p_{data}}log\frac{p_{data}}{p_{data}+p_{g}} - E_{x \sim p_{g}}log[ 1- \frac{p_{data}} {p_{data}+p_{g}}] \\ &= - E_{x \sim p_{data}}log\frac{p_{data}}{p_{data}+p_{g}} - E_{x \sim p_{g}}log[\frac{p_{g}}{p_{data}+p_{g}}] \\ &= 2log2 - D_{KL}[p_{data} \mid \mid \frac{p_{data} + p_{g}}{2}] - D_{KL}[p_{g} \mid \mid \frac{p_{data} + p_{g}}{2}]\\ &= 2log2 - 2D_{JS}(p_{data} \mid \mid p_{g}) \\ \end{align*}\]

즉, \(L^{(D^{*})}\) 를 최소화하는 것은 JS Divergence를 최대화 하는 것과 똑같다.

( Discriminator 입장에서는 두 분포가 최대한 다르게끔 인식되도록 노력한다! )

\(D^*(x) = \frac{p_{data}}{p_{data} + p_g}\) 식을 생각하면, 최적의 Discriminator는 \(D^*(x) = 0.5\) 이다.

하지만 문제점이 있다. 만약 두 분포 \(p_{data}\)와\(p_g\)가 서로 겹치는 영역이 없으면, 학습 과정에서 수렴하지 않게 될 것이다.

(1) Wesserstein Distance의 필요성

위에서 말했 듯, \(p_{data}\)와 \(p_g\)가 겹치지 않으면 수렴하지 않는 문제가 발생한다고 했다. 다음의 두 분포 예시를 통해 확인해보자.

• \(p_{data} = (x,y)\), \(x=0, y \sim U(0,1)\)
• \(p_g = (x,y)\), \(x=\theta, y\sim U(0,1)\)

위와 같은 두 분포가 주어졌을 때, 3가지 지표 (KL-Divergence, JS-Divergence, Wesserstein Distance)를 구하면 다음과 같다.

• \(D_{KL} (p_g \mid\mid p_data)\) = \(\sum 1 log \frac{1}{0}\) = \(+ \infty\)
• \(D_{JS}(p_{data} \mid \mid p_{g})\) = \(\frac{1}{2}\sum 1 log \frac {1}{0.5} + \frac{1}{2}\sum 1 log \frac {1}{0.5} = log2\)
• \(W(p_{data},p_{g})\) = \(\mid \theta \mid\)

\(D_{KL}\)은 무한대로 가고, \(D_{JS}\)는 상수형태가 되어버린다. 따라서 다음과 같이 두개의 분포가 겹치는 경우에는, (안정성 측면에 있어서) \(W\) 가 낫다고 할 수 있다.

(2) Wesserstein Distance (EMD)

우리는 \(p_{data}\) 와 \(p_g\)의 결합분포의 전체 집합인 \(\prod (p_{data},p_{g})\) 를 전부 활용하기 사실상 힘들다. 그래서 Kantorovich-Rubinstein Duality를 사용하여 다음과 같이 나타낼 수 있다.

( 아래에서 \(P_r\)는 real data, \(P_\theta\)는 fake data이다 )

https://image.slidesharecdn.com/wgangp-170529050013/95/nthu-ai-reading-group-improved-training-of-wasserstein-gans-10-638.jpg?cb=1496049172

K-Lipschitz Constratint :

\[\mid f(x_1) - f(x_2) \mid \leq K \mid x_1 - x_2 \mid\]

식은 복잡하지만, 쉽게 생각해보자. Discriminator의 목적인 “진짜는 맞게(1 로) 분류”, “가짜는 틀리게(0으로) 분류”하기 위해서, \(EMD(P_r,P_\theta)\)식의 구성 요소인 \(E_{x \sim P_r} f(x)\)는 크게, \(E_{x \sim P_\theta} f(x)\)는 작아져야 한다.

이를 활용하여, W를 정리하면 다음과 같다.

\[\begin{align*} W(p_{data}, p_g) &= \underset{w \in W}{max} E_{x \sim p_{data}}[f_{w}(x)] - E_{x \sim p_{g}}[f_{w}(x)]\\ &= \underset{w \in W}{max} E_{x \sim p_{data}}[D_{w}(x)] - E_{z}[D_{w}(G(z))]\\ \end{align*}\]

이제 이것을 우리는 새로운 Loss Function으로 사용할 것이고, 이것이 바로 WGAN이다.

(3) Summary of Loss Function

정리하면, Discriminator와 Generator의 Loss Function은 다음과 같다.

Discriminator

\[L^{(D)}= - E_{x\sim p_data}D_w(x) + E_z D_w(G(z))\]

Generator

\[L^{(G)}= - E_z D_w(G(z))\]

4. Algorithms of WGAN

• Until \(\theta\) converges..

  [ Discriminator ]

  • for t=1,…\(n_{critic}\) ( \(n_{critic}\) : Generator가 1회 반복하는 동안 Discriminator가 반복하는 횟수)
    • \(\{x^{(i)}\}_{i=1}^m \sim p_{data}\) 샘플링 ( m : batch size )
    • \(\{z^{(i)}\}_{i=1}^m \sim p_{z}\) 샘플링
    • caculcate gradient of Discriminator
    • update ( \(w \leftarrow w - \alpha \times RMSProp(w,g_w)\) ) ( WGAN에서는 Adam보다 RMS Prop을 사용하는 것이 더 안정적이라고 함 )
    • constraint on w ( \(w \leftarrow clip(w,-c,c)\) )
  • end for

  [ Generator ]

  • \(\{z^{(i)}\}_{i=1}^m \sim p_{z}\) 샘플링
  • caculcate gradient of Generator
  • update ( \(\theta \leftarrow \theta - \alpha \times RMSProp(\theta,G_{\theta})\))

• end while

5. GAN vs WGAN

https://miro.medium.com/max/3136/