5.Neural Machine Translation by Jointly Learning to Align and Translate (2016)
목차
- Abstract
- Introduction
- Background : NMT
- RNN Encoder-Decoder
- Learning to Align and Translate
- Decoder : General Description
- Encoder : Bidirectional RNN for Annotating Sequences
Abstract
NMT ( Neural Machine Translation )
- single NN that can be jointly tuned to maximize the translation performance
- often belong to encoder-decoders
- encoder ) encode a source sentece into fixed-length vector
- decoder ) generates translation
limitation : fixed-length context vector
\(\rightarrow\) propose to extend this! by allowing a model to automatically search for parts of a source sentence, that are relevant to predicting a target word
1. Introduction
most NMT = encoder-decoder network
problem : need to compress the informations into fixed-length vector!
( difficult for long sentences )
Introduce an extension to encoder-decoder model, which learns to “align and translate” jointly
( = finding out which part is relevant to get help answering the target word ? )
2. Background : NMT
Translation = finding a target sentence \(y\) that maximizes the conditional probability of \(y\) given a source sentence \(x\)
NMT based on RNNS with LSTM achieves SOTA
2-1. RNN Encoder-Decoder
[ Encoder ]
hidden state at time \(t\) : \(h_{t}=f\left(x_{t}, h_{t-1}\right)\).
context vector : \(c=q\left(\left\{h_{1}, \cdots, h_{T_{x}}\right\}\right)\).
- \(f\) and \(q\) are non-linear function
[ Decoder ]
predict the next word \(y_{t^{\prime}}\) given the context vector \(c\)
\(p(\mathbf{y})=\prod_{t=1}^{T} p\left(y_{t} \mid\left\{y_{1}, \cdots, y_{t-1}\right\}, c\right)\).
-
with RNN, \(p\left(y_{t} \mid\left\{y_{1}, \cdots, y_{t-1}\right\}, c\right)=g\left(y_{t-1}, s_{t}, c\right)\)
where \(g\) is a nonlinear function
3. Learning to Align and Translate
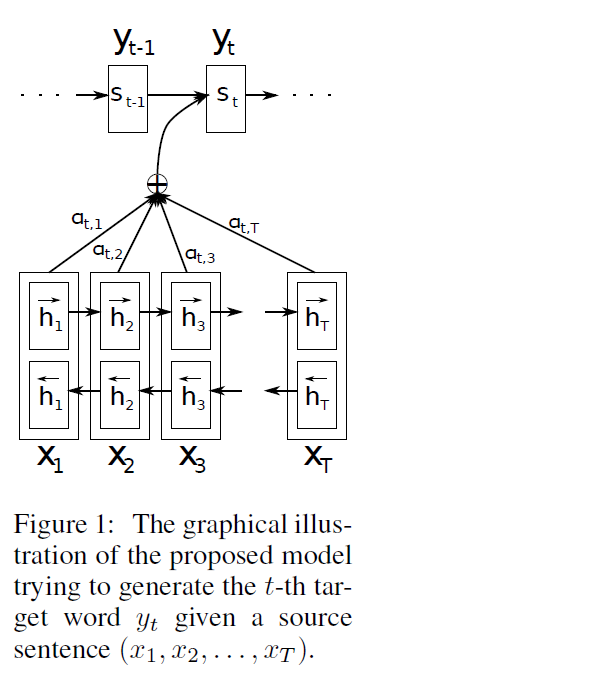
Encoder : bidirectional RNN
Decoder : emulates searching through a source sentence during decoding!
3-1. Decoder : General Description
Conditional Probability :
\(p\left(y_{i} \mid y_{1}, \ldots, y_{i-1}, \mathrm{x}\right)=g\left(y_{i-1}, s_{i}, c_{i}\right)\).
-
\(s_{i}=f\left(s_{i-1}, y_{i-1}, c_{i}\right)\) ) ……….. RNN hidden state for time \(i\)
-
\(c_{i}=\sum_{j=1}^{T_{x}} \alpha_{i j} h_{j}\). ….. context vector ( = weighted sum of \(h_i\)s )
-
\(\alpha_{i j}=\frac{\exp \left(e_{i j}\right)}{\sum_{k=1}^{T_{x}} \exp \left(e_{i k}\right)}\) ……… weight of each \(h_i\)
-
\(e_{i j}=a\left(s_{i-1}, h_{j}\right)\) ………. alignment model
( scores how well the inputs around poistion \(j\) and the output at position \(i\) matches )
-
-
-
3-2. Encoder : Bidirectional RNN for Annotating Sequences
would like the annotation (\(h_i\)) of each word to summarize not only the “preceding words”, but also the “following words”
\(\rightarrow\) use bidirectional RNN