InfoGAN (Interpretable Representation Learning by Information Maximizing GAN)

InfoGAN

1. Introduction

지금까지 봐왔던 GAN모델들은, 이미지가 주어졌을 때, 해당 이미지의 latent representation을 찾아내어 해당 이미지를 다시 복원할 수 있는 것에 초점을 맞췄다. (그래서 Loss Function들도 주로 ‘fake image’가 원본 이미지와 얼마나 유사한지를 기준으로 잡았었다). 하지만 앞으로 살펴볼 모델들은, 단순히 원본을 복원하는 것을 넘어서, 내가 원하는 대로 사진의 특성을 설정할수 있다는 점에서 보다 뛰어나다고 할 수 있다. 예를 들어, 사람의 얼굴 image를 input으로 받으면, 그 사진에서 “눈썹 모양”을 의미하는 latent vector, “입의 모양”을 의미하는 latent vector 등, input으로 들어온 사진을 분해하여 그에 해당하는 각각의 vector를 학습한다. 그 중 대표적인 InfoGAN과 StackedGAN에 대해서 살펴볼 것이고, 이번 포스트에서는 InfoGAN에 대해서 알아볼 것이다.

https://image.slidesharecdn.com/infogan-190408061341/95/infogan-interpretable-representation-learning-by-information-maximizing-generative-adversarial-nets-14-638.jpg?cb=1554704301

2. 분해된 표현의 GAN

우리는 여태까지 input image의 잠재 벡터(latent vector)를 찾아냈었다. 하지만 앞으로는 이 잠재벡터를, “해석 가능한 latent vector”와 “그렇지 못한 vector (noise)”로 나누어서 생각할 것이다.

모든 latent vector를 Z로 표현하고, 그 중

• 설명가능한 latent vector는 (1) c
• noise vector는 (2) z

로 표현하겠다.

여기서 추가할 가정은, “모든 설명가능한 latent vector c는 독립적이다”라는 것이다. 식으로 표현하면 다음과 같다.

\[p(c_1,c_2,..,c_L) = \prod_{i=1}^{L}p(c_i)\]

3. InfoGAN

InfoGAN의 핵심은 무엇일까? 직관적으로 생각해보면, 모든 latent vector Z에서 최대한 모든 벡터들을 설명가능하게끔 하는 것이다. 즉, 다르게 말하면 Z 중 c의 비중은 높고, z의 비중은 낮게 하는 것이다.

이를 다르게 표현하면, latent vector c와 , z와 c를 넣어서 생성된 image인 G(z,c)의 상호 정보를 최대화하는 것이라고 할 수 있다. 이 ‘상호 정보’의 정도를 다음과 같이 표현한다.

\(I(c ; G(z,c))\) ( = \(I(c; G(Z)))\) )

위 정보는 다음과 같은 식으로 표현할 수 있다.

\(I(c ; G(z,c))\) = \(H(c) - H(c \mid G(z,c)))\)

위의 \(H\)함수는 entropy값을 의미한다 ( entropy는 불확실성을 측정하는 지표로, 이 값이 높으면 ‘확률이 낮다, 즉 불확실하다’ 를 의미한다 )

우리는 위 식 \(I(c;G(z,c))\) 를 높이기 위해 \(H(c \mid G(z,c)))\) 값을 최소화 하면 된다 ( \(H(c)\)는 상수 취급한다 )

더 나아가기에 앞서서 Entropy에 대해서 알아보자.

Entropy

모든 사건 정보량의 기대값을 뜻함 ( 전체 사건의 확률분포의 불확실성의 양 )

\[H(P) = H(x) = E_{X \sim P}[I(x)] = E_{X\sim P}[-logP(x)] = -\sum_x P(x)logP(x)\] \[H(P,Q) = E_{X\sim P}[-logQ(x)] = -\sum_x P(x) logQ(x)\]

KL-Divergence에서도 위 두 식을 통해 나타낼 수 있다.

\[\begin{align*} D_{KL}(P\mid \mid Q) &= -\sum_x P(x) log(\frac{Q(X)}{P(X)})\\ &=-\sum_x P(x)\{logQ(x) - logP(x)) \}\\ &=-\sum_x \{P(x)logQ(x) - P(x)logP(x)) \}\\ &=-\sum_x P(x)logQ(x) + \sum_x P(x)logP(x)\\ &=H(P,Q) - H(P) \end{align*}\]

Conditional Entropy는 다음과 같이 표현할 수 있다.

\[\begin{align*} H(Y\mid X) &= \sum_{x,y}p(x,y)log(\frac{p(x)}{p(x,y)})\\ &=-\sum_{x,y}p(x,y)log(p(x,y)) + \sum_{x,y}p(x,y)log(p(x))\\ &= H(X,Y) + \sum_{x}p(x)(logp(x)))\\ &= H(X,Y) - H(X) \end{align*}\]

다시 돌아와서, \(H(c \mid G(z,c)))\)를 최소화해보자.

이 식은, 위에서 배운 Entropy와 KL-Divergence를 사용하면 다음과 같이 나타낼 수 있다.

\[H(c \mid G(z,c)) = H(G(z,c),c) - H(G(z,c)) = D_{KL}(G(z,c)\mid\mid c)\]

따라서, 우리는 다음과 같은 Lower Bound를 추정할 수 있다.

\[I(c; G(z,c)) \geq L(G,Q) = E_{c \sim P(c), x \sim G(z,c)}[logQ(c\mid x)] + H(c)\]

4. Loss Function of InfoGAN

GAN

• Discriminator의 Loss Function : \(L^{(D)} = - E_{x \sim P_{data}}logD(x) - E_z log(1-D(G(z)))\)
• Generator의 Loss Function : \(L^{(G)} = - E_zlogD(G(z))\)

InfoGAN

• Discriminator의 Loss Function : \(L^{(D)} = - E_{x \sim P_{data}}logD(x) - E_z log(1-D(G(z))) - \lambda I(c;G(z,c))\)
• Generator의 Loss Function : \(L^{(G)} = - E_zlogD(G(z)) - \lambda I(c;G(z,c))\)

각각의 Loss Function에 \(I(c;G(z,c))\) 와, 이를 조절해주는 parameter인 \(\lambda\)가 들어가는 것을 확인할 수 있다.

5. Summary

지금까지 배운 내용을 다음 사진 한 장으로 정리할 수 있다.

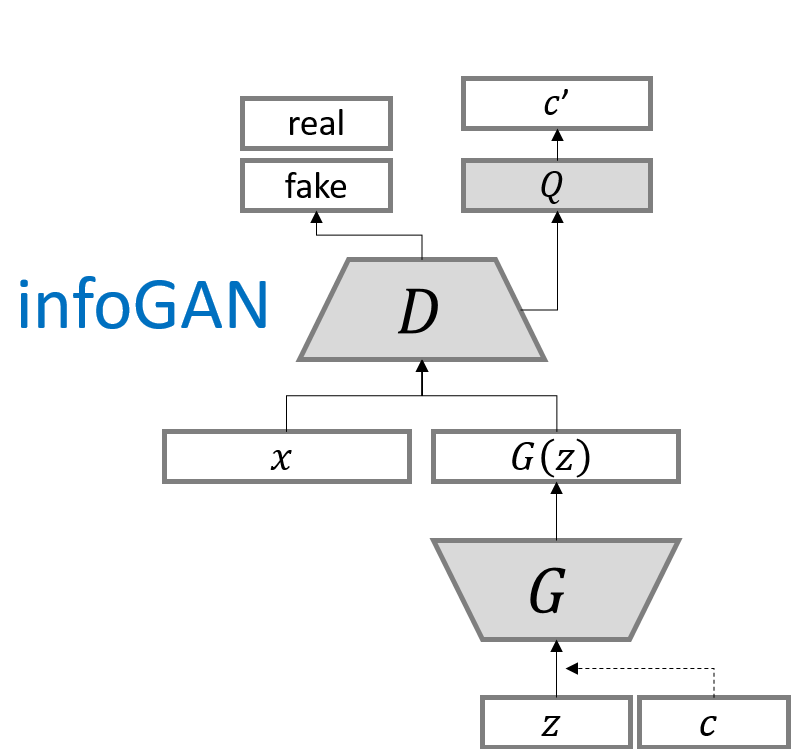
https://greeksharifa.github.io/public/img/2019-03-20-advanced-GANs/infoGAN1.png

위 그림에서 Q는, 상호정보 손실을 최소화 하기 위해서 훈련이 이루어진다. 이를 통해 새로 생성되는 c’과 c의 cross entropy를 줄여나가는 방향으로 update가 이루어진다.