20. Poly-encoders: Transformer Architectures and Pre-training Strategies for Fast and Accurate Multi-sentence Scoring (2020)
목차
- Abstract
- Introduction
- Method
- Transformers & Pre-training strategies
- Bi-encoder
- Cross-encoder
- Poly-encoder
Abstract
Deep pre-trained transformers
Tasks that make pairwise comparison between sequences, matching a given input with a corresponding label, 2 approachs are common :
- 1) Cross-encoders : perform full-attention over the pair
- better, but slower
- 2) Bi-encoders : encode the pair separately
This paper introduces POLY-encoder
1. Introduction
Trend : “Use of deep pre-trained LM, followed by fine-tuning”
Improvement to this approach for tasks that require multi-sentence scoring
Multi-sentence scoring
- def) given an input context, score a set of candidate lables
SOTA : BERT!
2 classes of fine-tuned architecture are typically built on top!
- 1) Cross-encoder (2019) : perform full (cross) attention
- 2) Bi-dencoder (2018) : input & candidate label separately, then combine at the end
This paper introduces 3) Poly-encoder
2. Methods
2-1. Transformers & Pre-training strategies
(1) Transformers
(2) Input representations
(3) Pre-training procedures
(4) Fine-tuning
-
after pre-training, one can fine-tune for multi-sentence selection task of choice
-
consider 3 architectures, with which we fine-tune the transformer
1) Bi-encoder, 2) Cross-encoder, 3) Poly-encoder
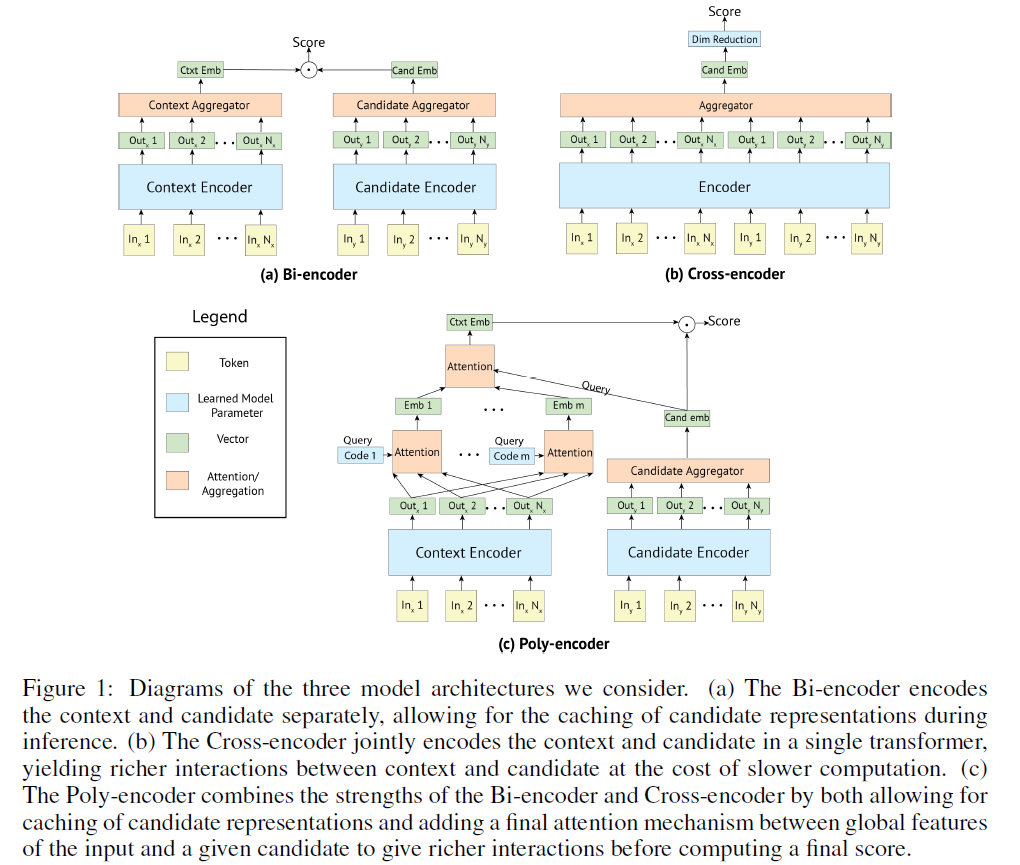
2-2. Bi-encoder
Input context & Candidate label are encoded into..
-
1) \(y_{c t x t}=\operatorname{red}\left(T_{1}(c t x t)\right)\)
-
2) \(y_{\text {cand }}=\operatorname{red}\left(T_{2}(\text { cand })\right)\)
where \(T_1\) & \(T_2\) are 2 transformers that have been pre-trained
\(red(\cdot)\) : function that reduces that sequence of vectors into one vector
3 ways of reducing the output into 1 representations via \(red(\cdot)\)
- 1) choose the first output of the transformer
- 2) compute the average over all outputs
- 3) average over the first \(m \leq N\) outputs
2-3. Cross-encoder
allows rich interaction between input context & candidate label
-
\(y_{c t x t, c a n d}=h_{1}=f i r s t(T(c t x t, c a n d))\).
\(first\) : function that takes the first vector of the sequence, produced by transformer
Scoring : \(s\left(\operatorname{ctxt}, \text { cand }_{i}\right)=y_{c t x t, c a n d_{i}} W\)
Inference Speed : does not allow for pre-computation of candidate embeddings ( not scalable )
2-4. Poly-encoder
\(y_{c t x t}^{i}=\sum_{j} w_{j}^{c_{i}} h_{j} \quad \text { where } \quad\left(w_{1}^{c_{i}}, . ., w_{N}^{c_{i}}\right)=\operatorname{softmax}\left(c_{i} \cdot h_{1}, . ., c_{i} \cdot h_{N}\right)\).
\(y_{c t x t}=\sum_{i} w_{i} y_{c t x t}^{i} \quad \text { where } \quad\left(w_{1}, \ldots, w_{m}\right)=\operatorname{softmax}\left(y_{\text {cand }_{i}} \cdot y_{c t x t}^{1}, . ., y_{\text {cand }_{i}} \cdot y_{c t x t}^{m}\right)\).
- using \(y_{\text {cand }_{i}}\) as query
