[Implicit DGM] 08. GAN

[Implicit DGM] 08. GAN

( 참고 : KAIST 문일철 교수님 : 한국어 기계학습 강좌 심화 2)

Contents

1. GAN 소개
2. Loss Function of GAN
3. Training of GAN

1. GAN 소개

( 아래의 그림 하나로, 설명은 생략한다 )

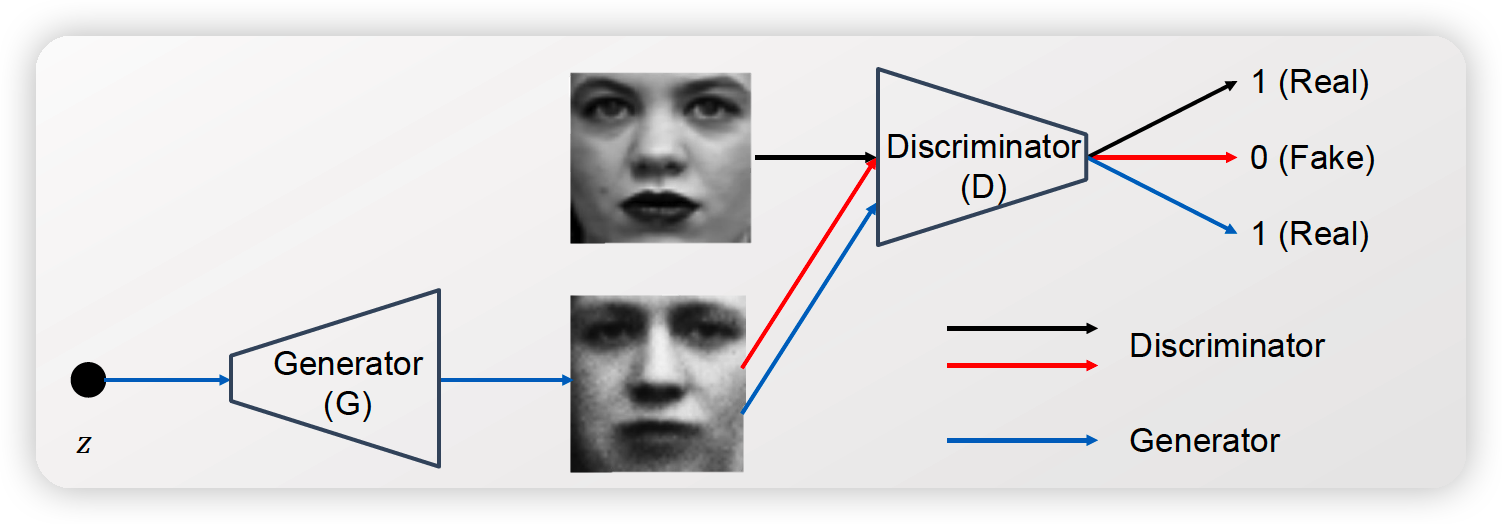
(1) Notation

\(G\left(z ; \theta_{g}\right)\) : generator

\(D\left(x ; \theta_{d}\right)\) : discriminator

• real data는 1로
• fake data는 0으로

\(p_{z}(z)\) : noise 샘플하는 prior

• ex) \(p_{z}(z) \sim N(0,1)\).

\(p_{\text {data }}(x)\) : data distribution

\(p_{g}(x)\) : \(G(z)\) 의 분포 ( where \(z \sim p_{z}\) )

(2) Loss Function

\(\min _{G} \max _{D} V(D, G)\),

• \(V(D, G)=E_{x \sim p_{\text {data }(x)}}[\log D(x)]+E_{Z \sim p_{z}(z)}[\log (1-D(G(z))]\).

(3) Analogy of GAN

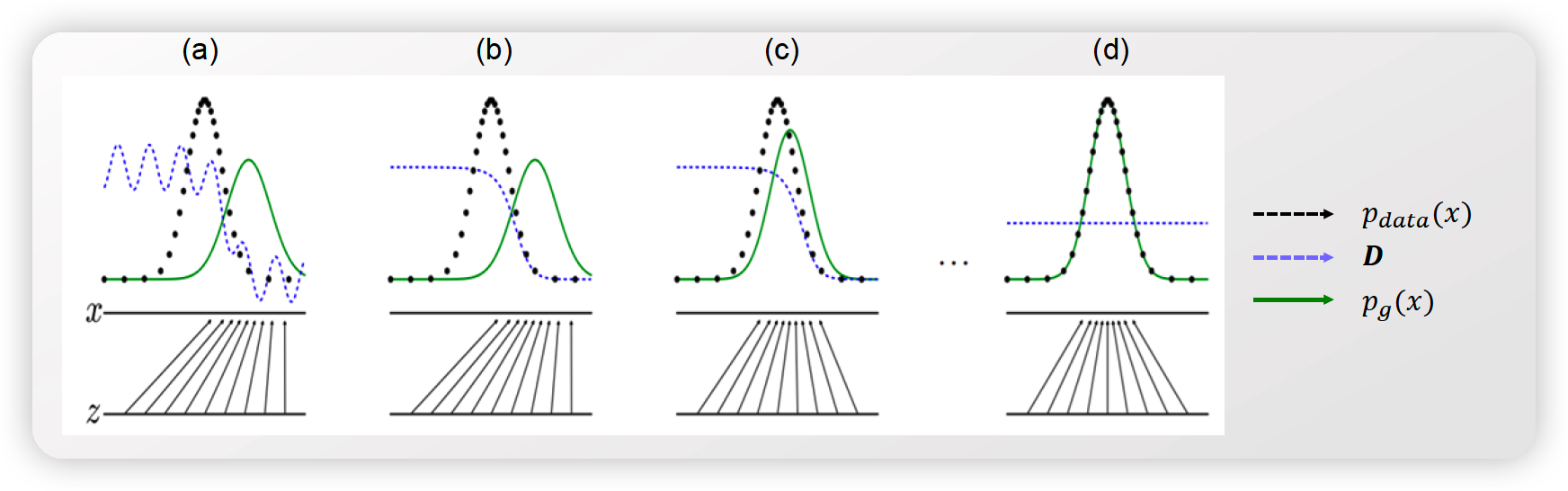
(a) prior에서 \(z\) 샘플 이후, generator에 넣기 ( \(G(z)=x\) )

(b) data들로부터 \(D\)를 학습

• real / fake를 잘 구분할 수 있도록

(c) \(D\)를 속이기 위해 \(G\)를 업데이트

(d) (ideal한 상태) 완벽한 \(G\) ( = data distribution과 같은 모양 )를 학습

• 이 둘 간의 구분이 불가함! \(D(x) = D(G(z)) = 0.5\)

2. Loss Function of GAN

[ 선수 지식 / notation ]

• \(K L(P \mid \mid Q) =\sum_{i} P(i) \ln \left(\frac{P(i)}{Q(i)}\right)\).
• \(z \sim p_{z}(z) \rightarrow x=G(z) \rightarrow x \sim P_{g}(x)\).
• \(D^{*}(x) =\frac{P_{\text {data }}(x)}{P_{g}(x)+P_{\text {data }}(x)}\).

위에서 간단히 봤던 GAN의 loss function을, 아래와 같이 정리해보자.

\[\begin{aligned} V(D, G)&=E_{x \sim p_{\text {data }(x)}}[\log D(x)]+E_{z \sim p_{z(z)}}[\log (1-D(G(z))] \\ &=\sum_{x} p_{\text {data }}(x) \ln \frac{P_{\text {data }}(x)}{P_{g}(x)+P_{\text {data }}(x)}+\sum_{x} p_{g}(x) \ln \left\{1-\frac{P_{\text {data }}(x)}{P_{g}(x)+P_{\text {data }}(x)}\right\} \\ &=\sum_{x} p_{\text {data }}(x) \ln \frac{P_{\text {data }}(x)}{P_{g}(x)+P_{\text {data }}(x)}+\sum_{x} p_{g}(x) \ln \left\{\frac{P_{g}(x)}{P_{g}(x)+P_{\text {data }}(x)}\right\} \\ &=\sum_{x} p_{\text {data }}(x) \ln \frac{P_{\text {data }}(x)}{2 \times \frac{P_{g}(x)+P_{\text {data }}(x)}{2}}+\sum_{x} p_{g}(x) \ln \frac{P_{g}(x)}{2 \times \frac{P_{g}(x)+P_{\text {data }}(x)}{2}} \\ &=\sum_{x} p_{\text {data }}(x) \ln \frac{P_{\text {data }}(x)}{\frac{P_{g}(x)+P_{\text {data }}(x)}{2}}+\sum_{x} p_{g}(x) \ln \frac{P_{g}(x)}{\frac{P_{g}(x)+P_{\text {data }}(x)}{2}}-\ln 2 \sum_{x} p_{\text {data }}(x)-\ln 2 \sum_{x} p_{g}(x) \\ &=K L\left(P_{\text {data }}(x) \mid \mid \frac{P_{g}(x)+P_{\text {data }}(x)}{2}\right)+K L\left(P_{g}(x) \mid \mid \frac{P_{g}(x)+P_{\text {data }}(x)}{2}\right)-2 \ln 2 \\ &=2 J S\left(P_{g} \mid \mid P_{\text {data }}\right)-\ln 4 \end{aligned}\]

Jensen-Shannon Divergence

\(J S(P \mid \mid Q)=\frac{1}{2} K L\left(P \mid \mid \frac{Q+P}{2}\right)+\frac{1}{2} K L\left(Q \mid \mid \frac{Q+P}{2}\right)\).

• (KL-divergence와는 달리) symmetric 하다
  • \(J S(P \mid \mid Q)=J S(Q \mid \mid P)\).
• (KL-divergence와는 달리) upper bound가 있다.
  • \(0 \leq J S(P \mid \mid Q) \leq \ln 2\).
• \(J S(P \mid \mid Q)=0\), if and only if \(P=Q\)

Jensen-Shannon Divergence & Information theory

Notation

• \(X\) : abstract function on the events
• \(M\) : mixture distribution
• \(Z\) : mode selection
  • 2 mode components : \(P\) & \(Q\)
• Mode proportion between \(Z=0\) & \(Z=1\) : uniform
  • \(X \sim M=\frac{P+Q}{2}\).

( Information gain \(I\) )

\(\begin{aligned} I(X ; Z)&=H(X)-H(X \mid Z)\\&=-\sum M \log M- (-\frac{1}{2}\left[\sum P \log P+\sum Q \log Q\right]) \\ &=-\sum \frac{P+Q}{2} \log M+\frac{1}{2}\left[\sum P \log P+\sum Q \log Q\right] \\ &=-\sum \frac{P}{2} \log M-\sum \frac{Q}{2} \log M+\frac{1}{2}\left[\sum P \log P+\sum Q \log Q\right] \\ &=\frac{1}{2} \sum P(\log P-\log M)+\frac{1}{2} \sum Q(\log Q-\log M) \\ &=\frac{1}{2} \sum P \log \frac{P}{M}+\frac{1}{2} \sum Q \log \frac{Q}{M}\\&=\frac{1}{2} K L(P \mid \mid M)+\frac{1}{2} K L(Q \mid \mid M)\\&=J S(P \mid \mid Q) . \end{aligned}\).

3. Training of GAN

(1) min-max problem

\(D\) 입장에서는 maximize ( = gradient ASCENT )

• \(\theta_{d}^{*}=\operatorname{argmax}_{\theta_{d}} E_{x \sim p_{\text {data }(x)}}\left[\log D\left(x ; \theta_{d}\right)\right]+E_{z \sim p_{z(z)}}\left[\log \left(1-D\left(G\left(z ; \theta_{g}\right) ; \theta_{d}\right)\right]\right.\).

\(G\) 입장에서는 minimize ( = gradient DESCENT )

• \(\theta_{g}^{*}=\operatorname{argmin}_{\theta_{g}} E_{z \sim p_{z(z)}}\left[\log \left(1-D\left(G\left(z ; \theta_{g}\right) ; \theta_{d}\right)\right]\right.\).

위 식에서 알 수 있듯, \(D\) 를 학습하기 위해선, \(G\)의 output ( = \(G\left(z ; \theta_{g}\right))\)이 필요하다.

이를 위해, 아래와 같은 2가지 방법을 생각해볼 수 있다.

• \(\theta_{d}\) and \(\theta_{g}\)를 동시에 학습

• \(\theta_{d}\) and \(\theta_{g}\)를 순차적으로 학습 ( 주로 이 방법으로 구현이 됨 )

(2) Theoretical results of GAN

\(V(D, G)=E_{x \sim p_{d a t a(x)}}[\log D(x)]+E_{Z \sim p_{z(z)}}[\log (1-D(G(z))]\).

• goal : \(\min _{G} \max _{D} V(D, G)\)
  • 위 식에서, \(C(G)=\max _{D} V(D, G)\)라 하자.

optimal \(D\) 하에서, global minimum은 달성된다

• global minimum \(\leftrightarrow\) \(p_g = p_{data}\)

• \[C(G) = -\log4\]

(3) Mode Collapse

generator가 특정한 이미지/데이터 하나로만 집중해서 생성하게 되는 상황을 말한다.

( 어떠한 \(z\)를 넣든간, \(D\)를 항상 속일 수 있는 특정 데이터만을 생성! )

\(G(z)=x^{*} \text { such that } x^{*}=\operatorname{argmax}_{x} D(x)\).

• regardless of \(z \sim p_{z(z)}\) sampling

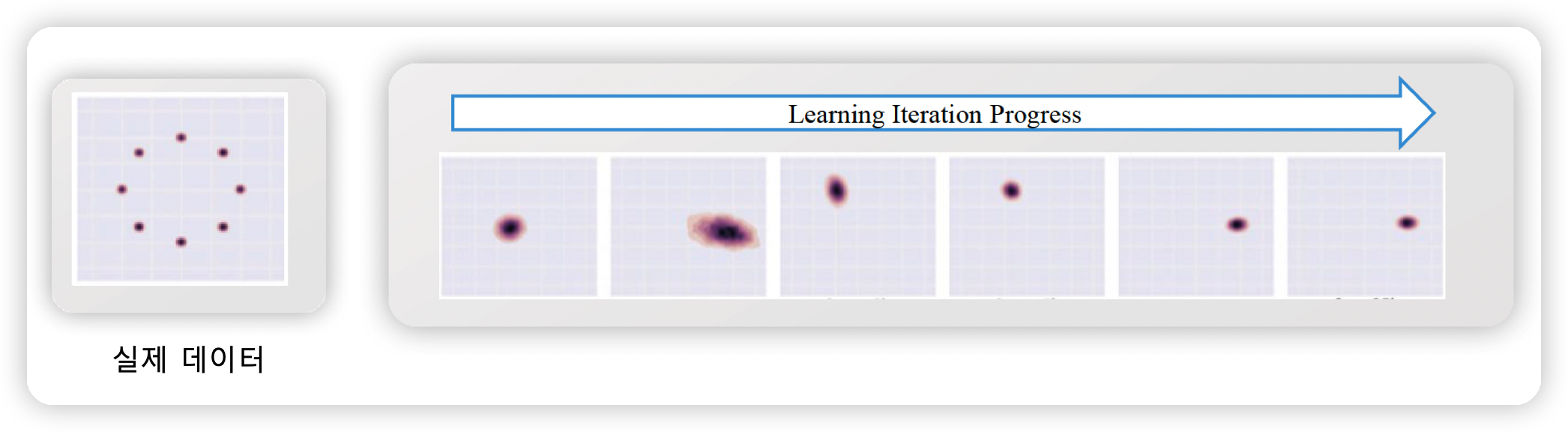
위 문제를 해결하기 위해 다양한 방법론들이 제안되어왔다.