[Implicit DGM] 09. Unrolled GAN

[Implicit DGM] 09. Unrolled GAN

( 참고 : KAIST 문일철 교수님 : 한국어 기계학습 강좌 심화 2)

Contents

1. Unrolling Discriminator Learning
2. Unrolled GAN
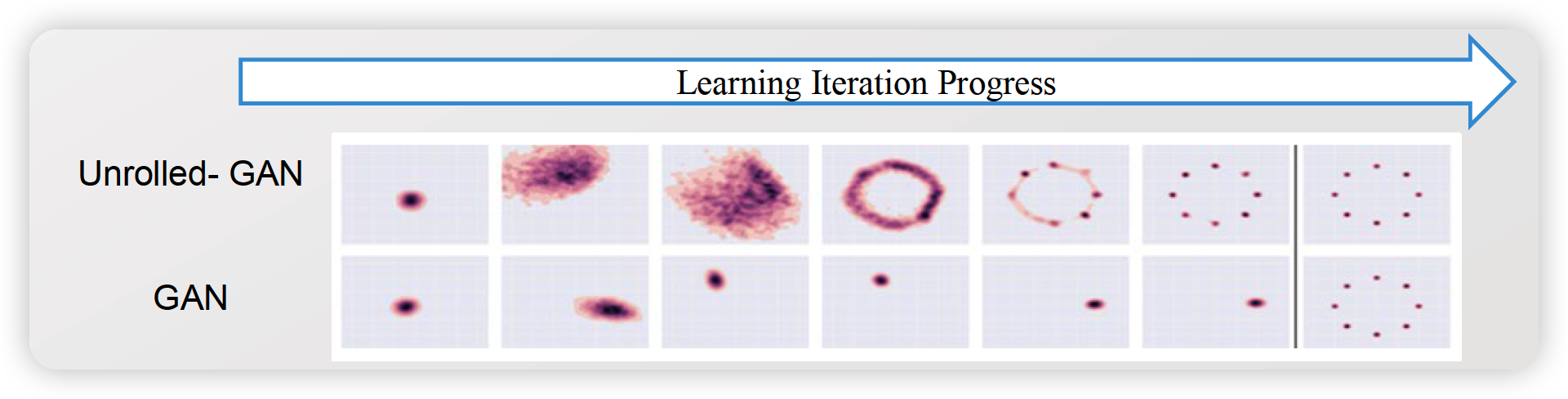
3. Effects on Mode Collapsing by Unrolled GAN

1. Unrolling Discriminator Learning

Vanilla GAN의 최적 parameter

\(\theta^{*}=\left\{\theta_{G}^{*}, \theta_{D}^{*}\right\}\).

• \(\theta_{G}^{*}=\operatorname{argmin} \max _{\theta_{G}} f\left(\theta_{G}, \theta_{D}\right)=\arg \min _{\theta_{G}} f\left(\theta_{G}, \theta_{D}^{*}\left(\theta_{G}\right)\right)\).
• \(\theta_{D}^{*}\left(\theta_{G}\right)=\arg \max _{\theta_{D}} f\left(\theta_{G}, \theta_{D}\right)\).

\(\rightarrow\) non-convex optimization problem으로, 하나의 global minimum에 도달하지 않을 수 있다.

\(G\)를 잘 학습하기 위해, 좋은 \(D\)를 얻어낼 수 있을까?

( \(D\)의 성능이 좋아야, \(G\)도 이에 걸맞는 뛰어는 생성자가 될 수 있기 때문에 )

\(\theta_{G}^{*}=\arg \min _{\theta_{G}} f\left(\theta_{G}, \theta_{D}^{*}\left(\theta_{G}\right)\right)\).

• 하지만…\(\theta_{D}^{*}\left(\theta_{G}\right)\)는 unreachable
• 때문에, 아래와 같이 근사$$를 해보자!
  • \(\theta_{D}^{0}=\theta_{D}\),
  • \(\theta_{D}^{k+1}=\theta_{D}^{k}+\eta^{k} \frac{d f\left(\theta_{G}, \theta_{D}^{k}\right)}{d \theta_{D}^{k}}\),
  • \(\theta_{D}^{*}\left(\theta_{G}\right)=\lim _{k \rightarrow \infty} \theta_{D}^{k}\),

Surrogate of \(f\left(\theta_{G}, \theta_{D}^{*}\left(\theta_{G}\right)\right): f_{K}\left(\theta_{G}, \theta_{D}\right)=f\left(\theta_{G}, \theta_{D}^{K}\left(\theta_{G}, \theta_{D}\right)\right)\)

• if \(k=0, f_{K}\left(\theta_{G}, \theta_{D}\right)=f\left(\theta_{G}, \theta_{D}\right)\)
• if \(k \rightarrow \infty, f_{K}\left(\theta_{G}, \theta_{D}\right)=f\left(\theta_{G}, \theta_{D}^{*}\left(\theta_{G}\right)\right)\)

2. Unrolled GAN

목표 : \(G\) 학습에 있어서, surrogate objective function를 도입함으로써, true generator objective에 가까워 지도록함

• (vanilla GAN의) \(G\)‘s objective : \(f\left(\theta_{G}, \theta_{D}\right)\)
• (Unrolled GAN의) \(G\)‘s objective : \(f\left(\theta_{G}, \theta_{D}^{K}\left(\theta_{G}, \theta_{D}\right)\right)\)

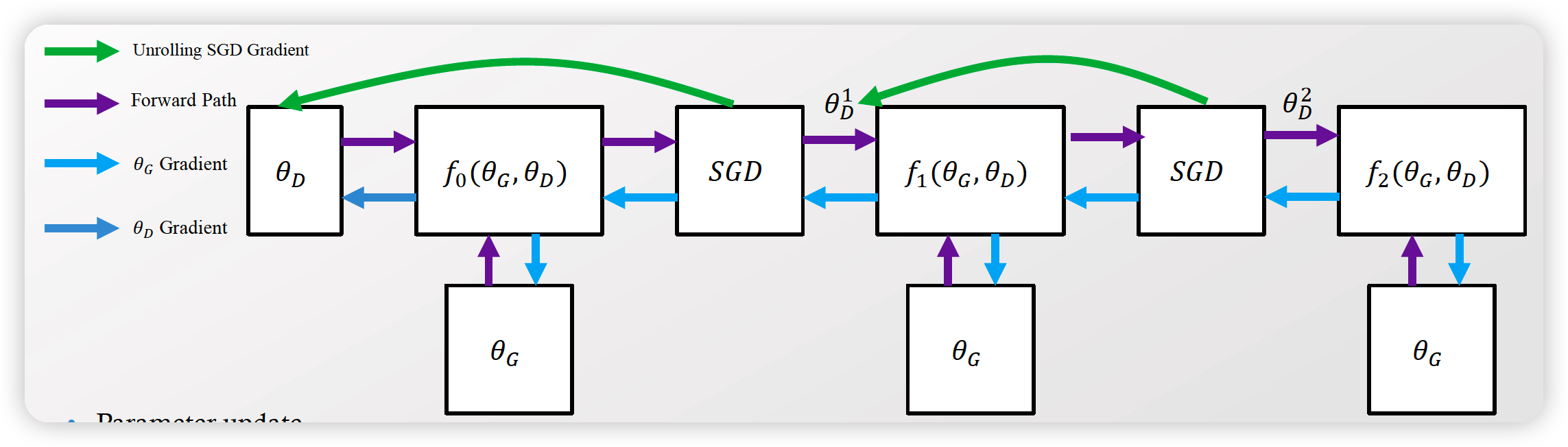
헷갈리지 말 것!

• 1번 업데이트하던 것을, 단순히 \(K\) 번 업데이트하는 것에 불과하다? NO!
• generator가 (향후 Kstep번 만큼) 업데이트 되었다고한다면 어땠을지를 미리 앞서서 고려한 것!

Parameter Update

\(\begin{aligned} &\theta_{G} \leftarrow \theta_{G}-\eta \frac{\mathrm{d} f_{K}\left(\theta_{G}, \theta_{D}\right)}{\mathrm{d} \theta_{G}} \\ &\theta_{D} \leftarrow \theta_{D}+\eta \frac{\mathrm{d} f\left(\theta_{G}, \theta_{D}\right)}{\mathrm{d} \theta_{D}} . \end{aligned}\).

Gradient 풀어보기

\(\frac{d f_{K}\left(\theta_{G}, \theta_{D}\right)}{d \theta_{G}}=\frac{\partial f\left(\theta_{G}, \theta_{D}^{K}\left(\theta_{G}, \theta_{D}\right)\right)}{\partial \theta_{G}}+\frac{\partial f\left(\theta_{G}, \theta_{D}^{K}\left(\theta_{G}, \theta_{D}\right)\right)}{\partial \theta_{D}^{K}\left(\theta_{G}, \theta_{D}\right)} \frac{d \theta_{D}^{K}\left(\theta_{G}, \theta_{D}\right)}{d \theta_{G}}\).

• as \(k \rightarrow \infty, \frac{\partial f\left(\theta_{G}, \theta_{D}^{K}\left(\theta_{G}, \theta_{D}\right)\right)}{\partial \theta_{D}^{K}\left(\theta_{G}, \theta_{D}\right)} \rightarrow 0\).

3. Effects on Mode Collapsing by Unrolled GAN