[Implicit DGM] 10. Variants of GAN

[Implicit DGM] 10. Variants of GAN

( 참고 : KAIST 문일철 교수님 : 한국어 기계학습 강좌 심화 2)

Contents

1. CGAN ( Conditional GAN )
2. InfoGAN ( Information Maximizing GAN )
3. CGAN vs InfoGAN

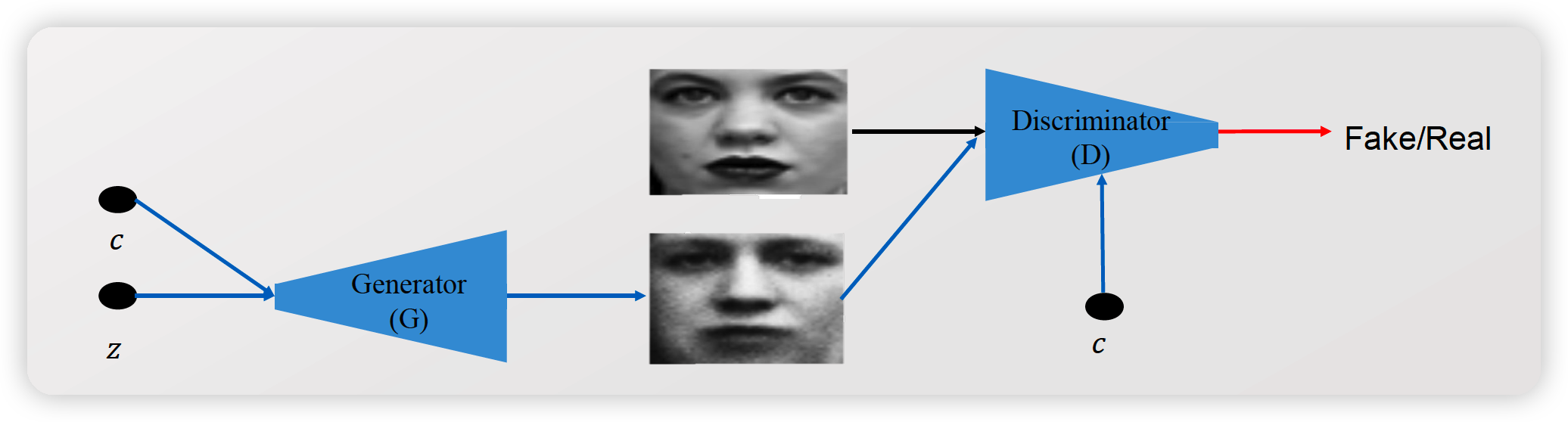
1. CGAN ( Conditional GAN )

아래의 두 포스트 참고하기

• https://seunghan96.github.io/dl/gan/CGAN/
• https://seunghan96.github.io/gan/(gan10)CGAN/

Original GAN

• \(\min _{G} \max _{D} V(D, G)=\min _{G} \max _{D} E_{x \sim p_{\text {data }(x)}}[\log D(x)]+E_{z \sim p_{z}(z)}[\log (1-D(G(z))]\).

Conditional GAN

• \(\min _{G} \max _{D} V(D, G) =\min _{G} \max _{D} E_{x \sim p_{\text {data }(x)}}[\log D(x \mid y)]+E_{z \sim p_{z}(z)}[\log (1-D(G(z \mid y))\).

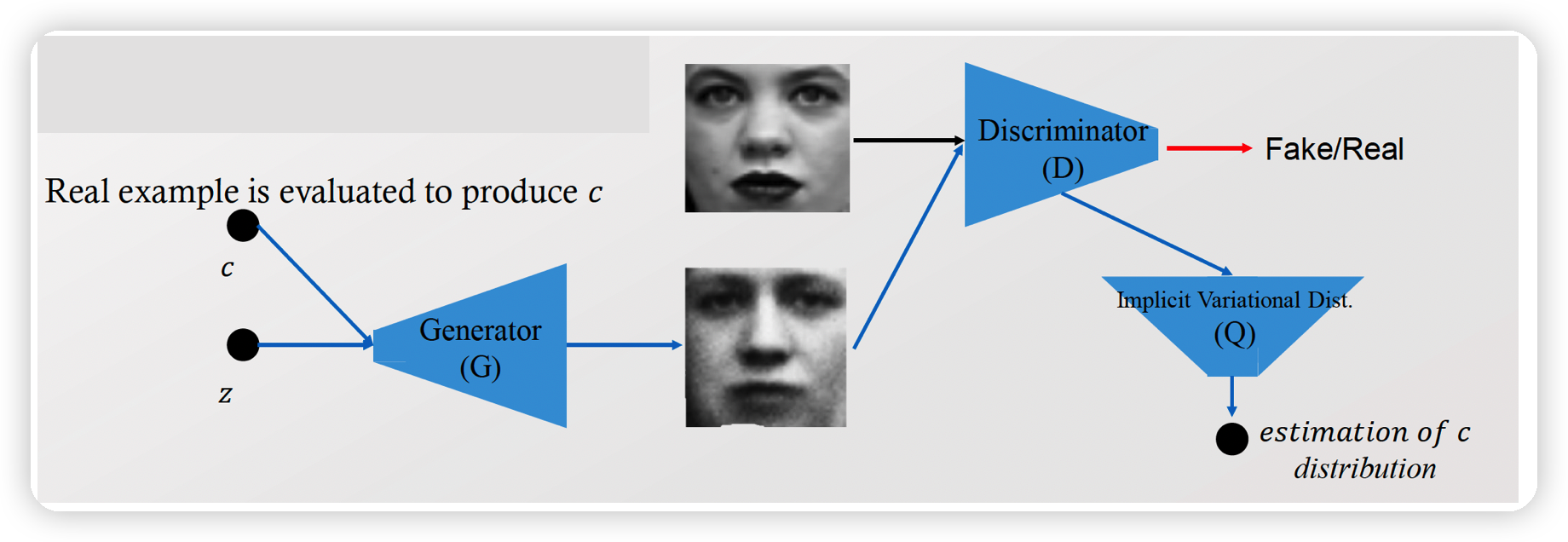
2. InfoGAN ( Information Maximizing GAN )

위의 1.CGAN 에서는, 우리가 가지고 있는 label 정보를 condition으로 넣었다.

그런데, 반드시 꼭 “observed”된 label만 condition으로 주어줄 수 있는 것인가? 그렇지 않다!!

InfoGAN은, latent variable을 GAN에 추가하는 방법론을 제안하였다.

(1) Mutual Information

\(\begin{aligned} I(X ; Z)&=D_{K L}\left(P_{X, Z} \mid \mid P_{X} \otimes P_{Z}\right)\\&=H(X)-H(X \mid Z)=H(Z)-H(Z \mid X) \end{aligned}\).

( Proof )

\(\begin{aligned} I(X ; Z)&=\sum_{x \in X, Z \in Z} P_{(X, Z)}(x, Z) \log \frac{P_{(X, Z)}(x, Z)}{P_{X}(x) P_{Z}(z)}\\ &=\sum_{x \in X, z \in Z} P_{(X, Z)}(x, z) \log \frac{P_{(X, Z)}(x, z)}{P_{X}(x)}-\sum_{x \in X, z \in Z} P_{(X, Z)}(x, z) \log P_{Z}(z)\\&=\sum_{x \in X, z \in Z} P_{X}(x) P_{Z \mid X=x}(z) \log P_{Z \mid X=x}(z)-\sum_{x \in X, z \in Z} P_{(X, Z)}(x, z) \log P_{Z}(z)\\ &=\sum_{x \in X} P_{X}(x)\left(\sum_{z \in Z} P_{Z \mid X=x}(z) \log P_{Z \mid X=x}(z)\right)-\sum_{z \in Z}\left(\sum_{x \in X} P_{(X, Z)}(x, z)\right) \log P_{Z}(z)\\&=-\sum_{x \in X} P_{X}(x) H(Z \mid X=x)-\sum_{z \in Z} P_{Z}(z) \log P_{Z}(z)\\ &=-H(Z \mid X)+H(Z) \end{aligned}\).

(2) Adding Latent Variable

Generator에 \(z\) 뿐만 아니라, latent variable \(c\) 또한 넣는 모델링을 생각해보자.

우리는, 생성되는 이미지가 이렇게 input으로 넣어준 \(c\) 와 관련이 있기를 바란다.

이러한 직관적인 아이디어에서 생각할 수 있는 목적 함수는 다음과 같다.

\[\min _{G} \max _{D} V(D, G)-\lambda I(c ; G(z, c))\]

• If \(c\) and \(G(z, c)\) are independent, \(I(c ; G(z, c))=0\)

(3) Variational Mutual Information Maximization

\(\begin{aligned} I(c ; G(z, c))&=H(c)-H(c \mid G(z, c)) \\ &=H(c)+E_{x \sim G(z, c)}\left[\sum_{c^{\prime} \sim P(c \mid x)} P\left(c^{\prime} \mid x\right) \log P\left(c^{\prime} \mid X\right)\right] \\ &=H(c)+E_{x \sim G(z, c)}\left[K L\left(P\left(c^{\prime} \mid x\right) \mid \mid Q\left(c^{\prime} \mid x\right)\right)+E_{c^{\prime} \sim P(c \mid x)}\left[\log Q\left(c^{\prime} \mid X\right)\right]\right] \\ &\geq E_{x \sim G(z, c)}\left[E_{c^{\prime} \sim P(c \mid x)}\left[\log Q\left(c^{\prime} \mid X\right)\right]\right]+H(c) \\ &=L_{I}(G, Q) \end{aligned}\).

• variational distribution \(Q\left(c^{\prime} \mid x\right)\) 를 도입했다.

위 Lower Bound를 사용하여, 아래와 같이 정리할 수 있다.

• \(\min _{G} \max _{D} V(D, G)-\lambda I(c ; G(z, c)) \leq \min _{G, Q} \max _{D} V(D, G)-\lambda L_{I}(G, Q)\).

  ( \(Q\)는 위 목적함수를 minimize 해야한다.)

(4) Implementation of InfoGAN

정리하자면, 우리의 optimization problem은 아래와 같다.

\(\min _{G, Q} \max _{D} V(D, G)-\lambda L_{I}(G, Q)\)

• \[L_{I}(G, Q)=E_{x \sim G(z, c)}\left[E_{c^{\prime} \sim P(c \mid x)}\left[\log Q\left(c^{\prime} \mid X\right)\right]\right]+H(c)\]
• \(Q\left(c^{\prime} \mid X\right)\) : \(X\)가 주어졌을 때, \(c\)를 생성하는 분포

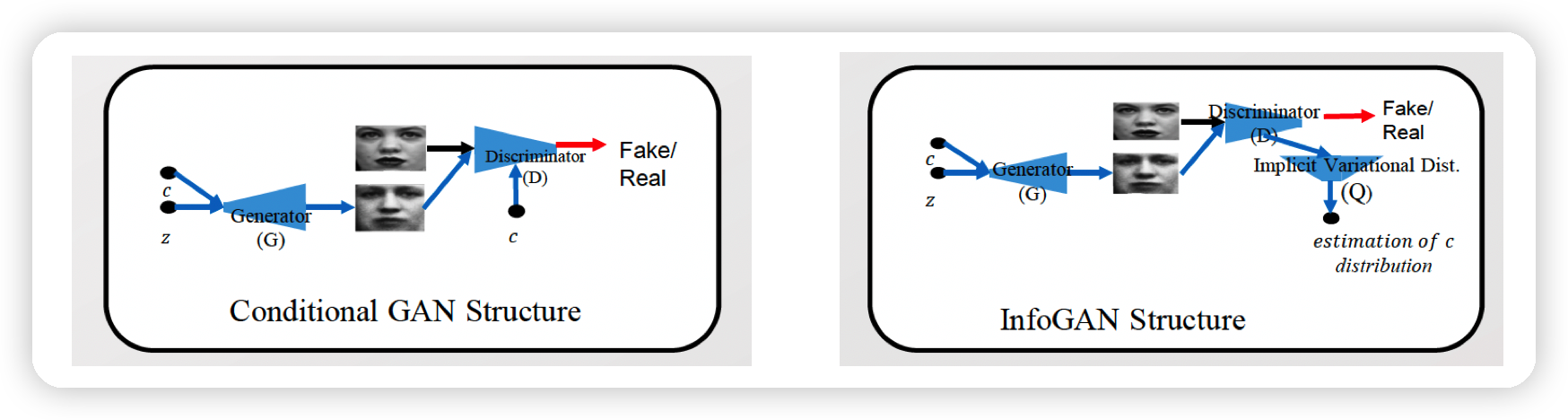
3. CGAN vs InfoGAN

공통점 : code를 추가적인 (\(G\)에 대한) input으로 가진다

CGAN

• goal : \(\min _{G} \max _{D} E_{x \sim p_{\text {data }(x)}}[\log D(x \mid y)]+E_{z \sim p_{z}(z)}[\log (1-D(G(z \mid y))]\)
• example)
  • \(G\)의 additional input
    • \(\mathrm{y}=[0,0,1,0,0,0,0,0,0,0], \mathrm{Z} \rightarrow \mathrm{G}(\mathrm{z}, \mathrm{y})=\mathrm{x}=\)image of ‘ 2 ‘
  • \(D\)의 aditional input
    • \(\mathrm{y}=[0,0,1,0,0,0,0,0,0,0], \mathrm{x}=\) image of ‘ 2 ‘ \(\rightarrow \mathrm{D}(\mathrm{y}, \mathrm{x})=\mathrm{p}\) in \([0,1]\)

InfoGAN

• goal : \(\min _{G, Q} \max _{D} V(D, G)-\lambda L_{I}(G, Q)\)

  ( \(\min _{G, Q} \max _{D} E_{x \sim p_{\text {data }(x)}}[\log D(x)]+E_{Z \sim p_{Z}(z)}[\log (1-D(G(z, c))]-\lambda\left\{E_{x \sim G(z, c)}\left[E_{c^{\prime} \sim P(c \mid x)}\left[\log Q\left(c^{\prime} \mid x\right)\right]\right]+H(c)\right\}\) )

• CGAN과의 차이점 :

  • \(D\)는 code를 input으로 받지 않는다

• Auxiliary structure

  • \(x=\) image of ‘ 2 ‘ \(\rightarrow \mathrm{Q}(\mathrm{c} \mid \mathrm{x})\)
  • \(\mathrm{Q}(\mathrm{c} \mid \mathrm{x})\) : pdf of \(c\) given \(x\)