[Implicit DGM] 11. Generalizing Loss of Divergence

[Implicit DGM] 11. Generalizing Loss of Divergence

( 참고 : KAIST 문일철 교수님 : 한국어 기계학습 강좌 심화 2)

Contents

1. Divergence
2. Convex Conjugate Function
3. \(f\)-divergence
4. Derivations of Optimal \(\tau\) of Fenchel Conjugate
5. Variational Divergence Minimization
6. Instantiation of Variational Divergence Minimization

1. Divergence

앞서 살펴봤듯, GAN의 loss function은 아래와 같이 JS-divergence의 형태를 띈다.

\(\begin{aligned} V(D, G)&=E_{x \sim p_{\text {data }(x)}}[\log D(x)]+E_{z \sim p_{z(z)}}[\log (1-D(G(z))]\\ &= 2 J S\left(P_{g} \mid \mid P_{\text {data }}\right)-\ln 4 \end{aligned}\),

계속 언급되는 표현인 “divergence”에 대해서 보다 자세히 알아보자.

• (1) 두 “분포 사이의 차이”

  • ex) KL-divergence, JS-divergence

• (2) “distance (거리)”와는 다른 개념이다.

  • “거리”라고 정의하기 위한 조건
    • 조건 1) \(d(x, y) \geq 0\) and \(d(x, y)=0 \Leftrightarrow x=y\)
    • 조건 2) \(d(x, y)=d(y, x)\)
    • 조건 3) \(d(x, y)+d(y, z) \geq d(x, z)\)
  • 이 중, divergence는 조건 1)만 만족한다

• (3) 두 분포 사이의 차이/거리 또한 일종의 “함수” (function)으로 볼 수 있다

Question : 어떻게 하면 이 “divergence 함수”를 일반화(generalize)할 수 있을까?

2. Convex Conjugate Function

Convex Duality

concave function \(f(x)\) ( ex. \(\log\) )는 …

• conjugate 혹은 dual function 형태로 나타낼 수 있다.

\(\begin{aligned} &f(x)=\min _{\lambda}\left\{\lambda^{T} x-f^{*}(\lambda)\right\} \\ &\Leftrightarrow f^{*}(\lambda)=\min _{x}\left\{\lambda^{T} x-f(x)\right\} \end{aligned}\).

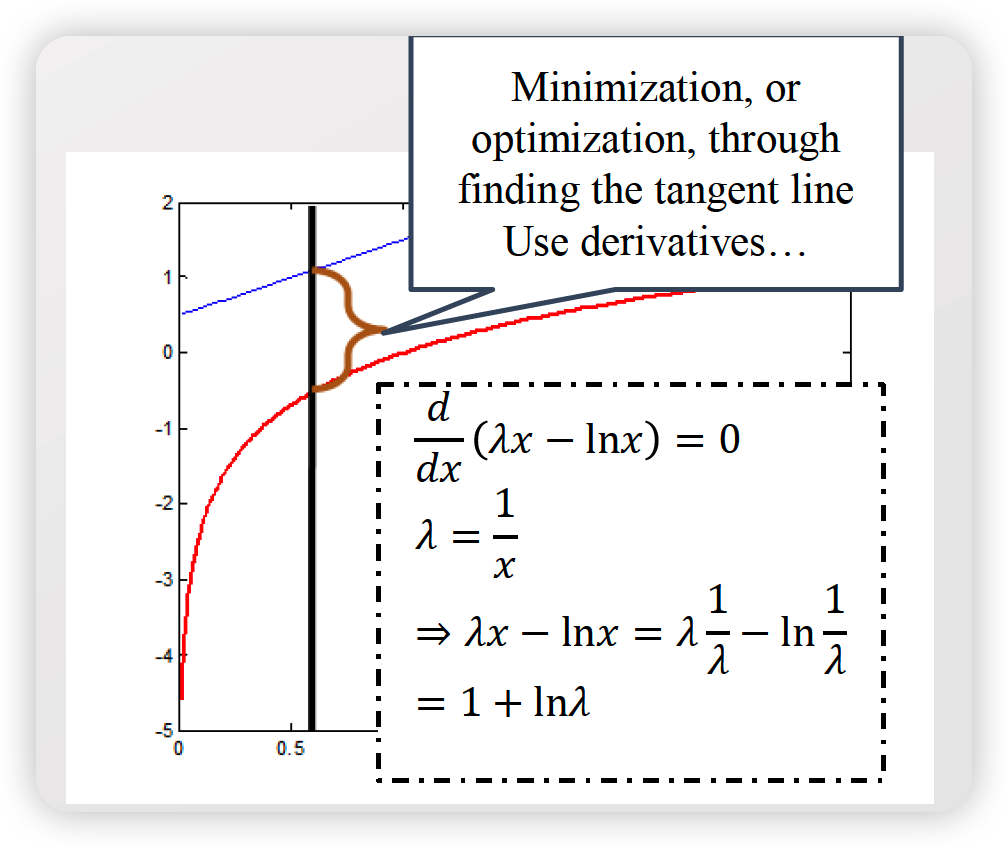
Convex Conjugate Function

어떤 함수 \(f: X \rightarrow R\) 가 있다고 하면,

이의 “convex conjugate function” \(f^{*}: X \rightarrow R\) 는 아래와 같다.

• \(f^{*}(a):=\sup \{<a,x>-f(x)\}\).

  ( 즉, \(f^{*}(a) \geq\{<a,x>-f(x) \}\) )

이는 다른 표현으로 Fenchel conjugate라고 한다. ( \(f\) 의 convexity와 무관하게 항상 convex하다 )

Conjugate Function의 특징

• (1) Fenchel Inequality

  • 임의의 함수 \(f\)와, 이의 convex conjugate function \(f^{*}\)에 대해,

    for all \(a, x \in X, f^{*}(a)+f(x) \geq\langle a, x\rangle\).

• (2) Order reversing

  • if \(f(x) \leq g(x)\) for all \(x \in X \Longrightarrow g^{*}(a) \leq f^{*}(a)\) for all \(a \in X\)

• (3) \(f^{*}\) 는 항상 convex & lower semi-continuous

• (4) 기타 : \(a= f^{'}(x)\) 로 설정할 경우, Inequality식에서 등식이 성립한다!

위의 (4) 증명 :

\(\begin{aligned} a=f^{\prime}(x) \Rightarrow \forall y & \in X, f(y) \geq f(x)+<a, y-x>\\ & \Leftrightarrow<a, y>-f(y) \leq<a, x>-f(x) \\ & \Leftrightarrow \sup _{y \in X}\{<a, y>-f(y)\}=f^{*}(a) \leq<a, x>-f(x) \\ & \Leftrightarrow f^{*}(a)+f(x) \leq<a, x>\Leftrightarrow f^{*}(a)+f(x)=<a, x> \end{aligned}\).

3. \(f\)-divergence

지금까지 여러 종류의 divergence들에 대해 살펴본 적이 있다.

이 모든 divergence들을, 아래와 같은 일반적인 general form으로 나타낼 수 있다.

이를 \(f\)-divergence라고 한다.

\(D_{f}(P \mid \mid Q)=\int_{x} q(x) f\left(\frac{p(x)}{q(x)}\right) d x\).

• \(f\) : “convex”한 generator function
• \(f(1)=0\) : 두 분포가 완전히 일치하면, divergence=0이 된다는 조건

이 generator function \(f\)에 대해서도, (위에서 배웠던) Fenchel conjugate 인 \(f^{*}\) 도 설정할 수 있다.

• (복습) \(f(u)=\sup _{t \in T}\left\{t u-f^{*}(t)\right\}\)

\(f\) divergence를 아래와 같이 전개해볼 수 있다.

\(\begin{array}{rl} D_{f}(P \mid \mid Q)&=\int_{x} q(x) f\left(\frac{p(x)}{q(x)}\right) d x\\&=\int_{x} q(x) \sup _{t \in T}\left\{t \frac{p(x)}{q(x)}-f^{*}(t)\right\} d x \\ & \geq \sup _{\tau \in \operatorname{dom}_{f^{*}}}\left\{\int_{x} p(x) \tau(x) d x-\int_{x} q(x) f^{*}(\tau(x)) d x\right\} \\ & =\sup _{\tau \in d o m_{f^{*}}}\left\{E_{x \sim p(x)}[\tau(x)]-E_{x \sim q(x)}\left[f^{*}(\tau(x))\right]\right\} \end{array}\).

정리

• domain of \(f\) : \(\mathrm{u}=\frac{p(x)}{q(x)} \in\) dom \(_{f}\) \(t\)

• \(t ( = \tau(x) )\) 는 \(x\)에 따라 변화한다.

  • \(\tau: X \rightarrow R\).

  • 최적의 \(\tau(x)\)는 ?

    \(\rightarrow\) \(\tau(x)=f^{\prime}\left(\frac{p(x)}{q(x)}\right)\) ( 이와 같이 설정할 경우, equality가 성립함을 위에서 보였었다 )

• 데이터

  • \(p(x)\) : REAL image
  • \(q(x)\) : FAKE image

우리는 \(P\) & \(Q\) 사이의 Divergence를 최소화 하고 싶다.

보다 정교한 divergence값을 위해, lower bound를 maximize해서 최대한 tight하게 하고 싶다.

이를 위해, inequality식에서 등식이 만족하는 조건인 \(\tau(x)=f^{\prime}\left(\frac{p(x)}{q(x)}\right)\) 로 설정한다.

4. Derivations of Optimal \(\tau\) of Fenchel Conjugate

Family of \(f\)-divergence :

• \(D_{f}(P \mid \mid Q)=\int_{x} q(x) f\left(\frac{p(x)}{q(x)}\right) d x\).

(1) KL-divergence

\(D_{f}(P \mid \mid Q)=\int p(x) \log \frac{p(x)}{q(x)} d x\).

• \(f(u)=u \log u\).
• \(f^{\prime}(u)=\log u+u \frac{1}{u}=1+\log u\).

\(\rightarrow\) 최적의 \(\tau(x)\) : \(\tau(x)=f^{\prime}\left(\frac{p(x)}{q(x)}\right)=1+\log \frac{p(x)}{q(x)}\).

(2) GAN divergence

\(\begin{aligned} V(D, G)&=E_{x \sim p_{\text {data }(x)}}[\log D(x)]+E_{z \sim p_{z(z)}}[\log (1-D(G(z))]\\ &=\int p(x) \log \frac{p(x)}{p(x)+q(x)}+q(x) \log \frac{q(x)}{p(x)+q(x)} d x\\ &=\int p(x) \log \frac{2 p(x)}{p(x)+q(x)}+q(x) \log \frac{2 q(x)}{p(x)+q(x)}-p(x) \log 2-q(x) \log 2 d x\\ &=\int p(x) \log \frac{2 \frac{p(x)}{q(x)}}{\frac{p(x)}{q(x)}+1}+q(x) \log \frac{2}{\frac{p(x)}{q(x)}+1} d x-\log 4\\ &=\int p(x) \log \frac{p(x)}{q(x)}-(p(x)+q(x)) \log \left(\frac{p(x)}{q(x)}+1\right)+(p(x)+q(x)) \log 2 d x-\log 4\\ &=\int q(x)\left\{\frac{p(x)}{q(x)} \log \frac{p(x)}{q(x)}-\left(\frac{p(x)}{q(x)}+1\right) \log \left(\frac{p(x)}{q(x)}+1\right)\right\} d x \end{aligned}\).

• \(f(u)=u \log u-(u+1) \log (u+1)\).
• \(f^{\prime}(u)=1+\log u-\log (u+1)-(u+1) \frac{1}{u+1}=\log \frac{u}{u+1}\).

\(\rightarrow\) 최적의 \(\tau(x)\) : \(\tau(x)=f^{\prime}\left(\frac{p(x)}{q(x)}\right)=\log \frac{p(x)}{p(x)+q(x)}\)

\(\tau(x)=\log \frac{p(x)}{p(x)+q(x)}\) 식은 낯에 익다.

GAN의 discriminator에서 본적 있는 식이다.

• \(D^{*}(x)=\frac{P_{d a t a}(x)}{P_{g}(x)+P_{d a t a}(x)}\).

5. Variational Divergence Minimization

우리는 \(f\)-divergence를 direct하게 optimize할 수 없다

따라서, 우리는 lower bound를 optimize하는 방식으로 진행할 것이다.

[ 근사할 필요 X 함수 ]

• \(p(x)\) : REAL 샘플 데이터 분포
• \(f^{*}(t)\) : \(f(u)\) 의 Fenchel conjugate
  • \(f\)함수 결정과 동시에 자동으로 결정됨

[ 근사할 필요 O 함수 ]

• \(\boldsymbol{q}(\boldsymbol{x})\) : FAKE 샘플 데이터 생성자
  • \(z \sim p(z), x_{\text {gen }}=G(z)\),
• \(\boldsymbol{\tau}(\boldsymbol{x})\) : \(x\)에 따라 바뀌는 함수
  • 질문 : 어… \(\tau(x)=f^{\prime}\left(\frac{p(x)}{q(x)}\right)=\log \frac{p(x)}{p(x)+q(x)}\) 라고 아까 정하지 않았었나?
  • 답 : 그건 “optimal”하기 위한 조건! 실제로 그렇게 되기는 어려우므로, 함수를 사용해서 저 optimal 값에 근사하는 일종의 함수를 학습하는 것이다! 해당 함수는, 위 식에서 알 수 있듯 \(p(x)\) 와 \(q(x)\)를 구분하는 classifier일 것이다.

Parameterized version of the lower bound

\(F(\theta, \omega)=E_{x \sim P}\left[T_{\omega}(x)\right]-E_{x \sim Q_{\theta}}\left[f^{*}\left(T_{\omega}(x)\right)\right]\).

( 기존 GAN의 목적함수 : \(E_{x \sim p_{\text {data }(x)}}[\log D(x)]+E_{z \sim p_{z(z)}}[\log (1-D(G(z))]\) )

• MINIMIZE ( main goal )
  • divergence줄이기 위해!
  • 즉, \(\theta\) 를 학습하기 위해
• MAXIMIZE ( sub goal )
  • 보다 정확한 (tight한) lower bound를 얻기 위해
  • 즉, 최적의 \(\tau\)를 학습하기 위해 ( \(\tau\)의 파라미터 : \(\omega\) )

6. Instantiation of Variational Divergence Minimization

Instantiation of GAN divergence

• \(f(u)=u \log u-(u+1) \log (u+1)\).
• \(\tau(x)=f^{\prime}\left(\frac{p(x)}{q(x)}\right)=\log \frac{p(x)}{p(x)+q(x)}\).
  • \(T_{\omega}(x)\) : NN
    • 이 NN의 output은 \(f^{*}\)에 대한 input으로써 사용된다.

\[\begin{aligned}f^{*}(t)&=\sup _{u \in U}\{u t-f(u)\}\\&=\sup _{u \in U}\{u t-u \log u+(u+1) \log (u+1)\} \end{aligned}\]

위 \(f^{*}(t)\) 식을 정리해보자.

• let \(g(t, u)=u t-u \log u+(u+1) \log (u+1)\).

• \(g(t,u)\)에 대한 1,2차 미분

  • (1차) \(\frac{d g(t, u)}{d u}=t-\log u-u \frac{1}{u}+(u+1) \frac{1}{u+1}+\log (u+1)=t+\log \frac{u+1}{u}\).
  • (2차) \(\frac{d^{2} g(t, u)}{(d u)^{2}}=\frac{1}{u+1}-\frac{1}{u}<0\)
    • concave 함수이다.

• \(\frac{d g(t, u)}{d u}=0 \rightarrow t=\log \frac{u}{u+1} \rightarrow t<0\).

• 이를 대입하면,

  • \(g(t, u)=u t-u \log \frac{u}{u+1}+\log (u+1)=u t-u t+\log (u+1)\).

  • \(f^{*}(t)=g(t)=-\log \left(1-e^{t}\right)\),

    \(\rightarrow\) 따라서, \(T_{\omega}(x)\)는 \(R_{-}\)의 범위에 있어야 한다.

\(\rightarrow\) negative softplus : \(a(x)=-\log \left(1+e^{x}\right)\)