[Paper Review] 17.(Analysis,Manipulation) On the STEERABILITY of GANs

[Paper Review] 17. On the STEERABILITY of GANs

Contents

1. Abstract
2. Introduction
3. Method
   1. Objective
   2. Reducing Transformation Limits

0. Abstract

recent GANs : can synthesize very realistic & diverse images

BUT….. fall short of being COMPREHENSIVE models of the visual manifold

This paper :

• study GAN’s ability to fit simple transformations,

  such as camera movements and color changes

• by steering in the latent space, can shift the distn, while still creating realistic images

1. Introduction

kinds of transformation this paper explores :

By moving in some direction of GAN latent space, can we hallucinate walking toward this dog?

• YES!
• but… if dog face fills the FULL frame…. FAIL!

Reason : due to biases in the distn of images, on which GAN is trained

This paper seeks to quantify the degree to which we can achieve basic visual transformations by navigating in GAN latent space

In other words, are GANs “STEERABLE” in latent space?

Contribution

1. simple walk in latent space \(\rightarrow\) achieves camera motion & color transformations
2. linear walk = as effective as more complex non-linear walks

2. Method

Goal : achieve transformations in the output space, by moving in the latent space

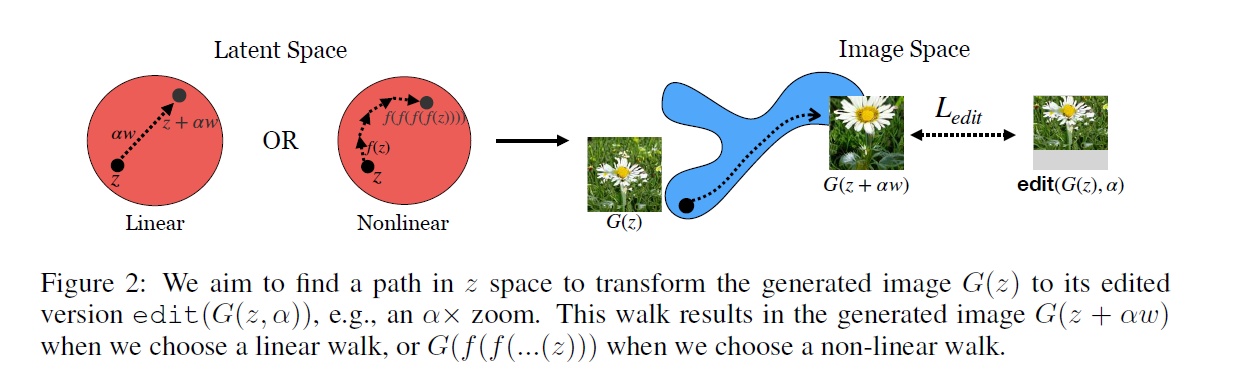
(1) Objective

• want to learn \(N\)-dim vector, representing the optimal path for a given transformation
  • multiply \(\alpha\) : step size

LINEAR version

• learn the walk \(w\), by minimizing…
  • \(w^{*}=\underset{w}{\arg \min } \mathbb{E}_{z, \alpha}[\mathcal{L}(G(z+\alpha w), \operatorname{edit}(G(z), \alpha))]\).
• (1) generated images, after taking \(\alpha\) step in latent direction = \(G(z+\alpha w)\).

• (2) target, derived from source image \(G(z)\) = edit \((G(z), \alpha)\).

• model \((\alpha)=G\left(z+\alpha w^{*}\right)\).
  • optimized transformation vector \(w^{*}\) with the step size \(\alpha\)

NON-LINEAR version

• learn a function, \(f^{*}(z)\) ( = small \(\epsilon\)-step transformation edit \((G(z), \epsilon)\) )
• minimize..
  • \(\mathcal{L}=\mathbb{E}_{z, n}\left[ \mid \mid G\left(f^{n}(z)\right)-\operatorname{edit}(G(z), n \epsilon)\right) \mid \mid ]\).

(2) Reducing Transformation Limits

Review

• linear : \(w^{*}=\underset{w}{\arg \min } \mathbb{E}_{z, \alpha}[\mathcal{L}(G(z+\alpha w), \operatorname{edit}(G(z), \alpha))]\)
• nonlinear : \(\mathcal{L}=\mathbb{E}_{z, n}\left[ \mid \mid G\left(f^{n}(z)\right)-\operatorname{edit}(G(z), n \epsilon)\right) \mid \mid ]\)

\(\rightarrow\) both keep the model weights fixed!

a) Explore adding data augmentations!

• by editing the training images with each corresponding transformations

b) also introduce modified objective function

• that jointly optimizes G weights & linear walk vector

• \(G^{*}, w^{*}=\arg \min _{G, w}\left(\mathcal{L}_{\text {edit }}+\mathcal{L}_{G A N}\right)\).

• \(\mathcal{L}_{\text {edit }}=L 2(G(z+\alpha w)-\operatorname{edit}(G(z), \alpha))\).

( error between "learned transformation" & "target image" )

• \(\mathcal{L}_{G A N}=\max _{D}\left(\mathbb{E}_{z, \alpha}[D(G(z+\alpha w))]-\mathbb{E}_{x, \alpha}[D(\operatorname{edit}(x, \alpha))]\right)\).

( discriminator error )